A Survey of Risk-Aware Multi-Armed Bandits

In several applications such as clinical trials and financial portfolio optimization, the expected value (or the average reward) does not satisfactorily capture the merits of a drug or a portfolio. In such applications, risk plays a crucial role, and a risk-aware performance measure is preferable, so as to capture losses in the case of adverse events. This survey aims to consolidate and summarise the existing research on risk measures, specifically in the context of multi-armed bandits. We review various risk measures of interest, and comment on their properties. Next, we review existing concentration inequalities for various risk measures. Then, we proceed to defining risk-aware bandit problems, We consider algorithms for the regret minimization setting, where the exploration-exploitation trade-off manifests, as well as the best-arm identification setting, which is a pure exploration problem -- both in the context of risk-sensitive measures. We conclude by commenting on persisting challenges and fertile areas for future research.

Best Arm Identification in Restless Markov Multi-Armed Bandits

We study the problem of identifying the best arm in a multi-armed bandit environment when each arm is a time-homogeneous and ergodic discrete-time Markov process on a common, finite state space. The state evolution on each arm is governed by the arm's transition probability matrix (TPM). A decision entity that knows the set of arm TPMs but not the exact mapping of the TPMs to the arms, wishes to find the index of the best arm as quickly as possible, subject to an upper bound on the error probability. The decision entity selects one arm at a time sequentially, and all the unselected arms continue to undergo state evolution ({\em restless} arms). For this problem, we derive the first-known problem instance-dependent asymptotic lower bound on the growth rate of the expected time required to find the index of the best arm, where the asymptotics is as the error probability vanishes. Further, we propose a sequential policy that, for an input parameter $R$, forcibly selects an arm that has not been selected for $R$ consecutive time instants. We show that this policy achieves an upper bound that depends on $R$ and is monotonically non-increasing as $R\to\infty$. The question of whether, in general, the limiting value of the upper bound as $R\to\infty$ matches with the lower bound, remains open. We identify a special case in which the upper and the lower bounds match. Prior works on best arm identification have dealt with (a) independent and identically distributed observations from the arms, and (b) rested Markov arms, whereas our work deals with the more difficult setting of restless Markov arms.

Optimal Clustering with Bandit Feedback

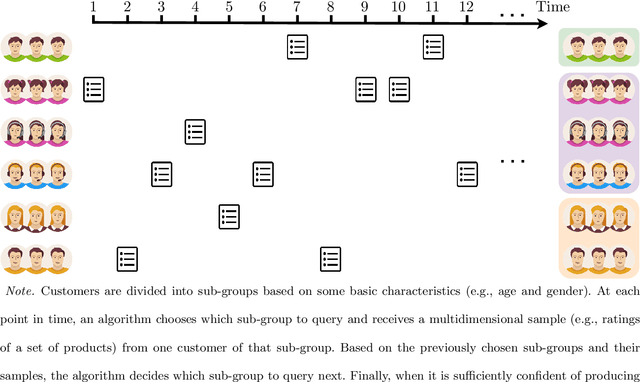
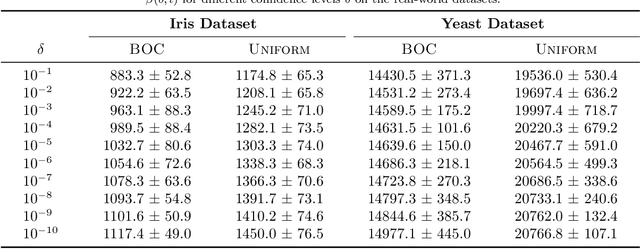
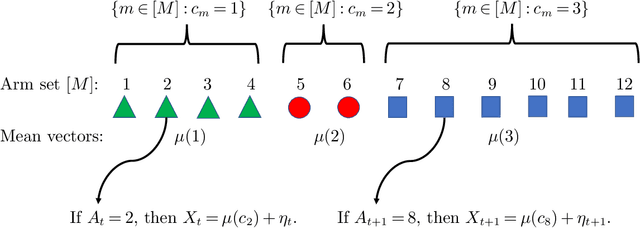
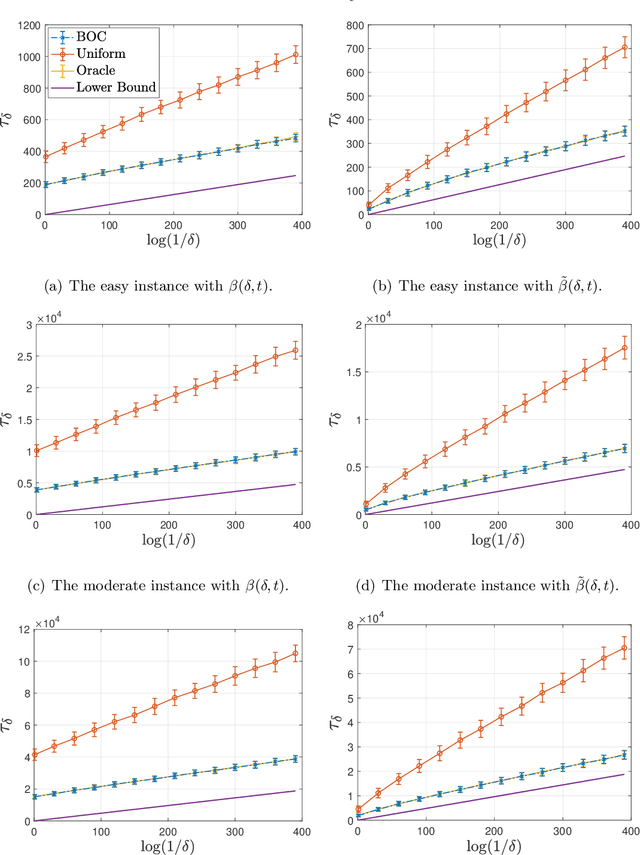
This paper considers the problem of online clustering with bandit feedback. A set of arms (or items) can be partitioned into various groups that are unknown. Within each group, the observations associated to each of the arms follow the same distribution with the same mean vector. At each time step, the agent queries or pulls an arm and obtains an independent observation from the distribution it is associated to. Subsequent pulls depend on previous ones as well as the previously obtained samples. The agent's task is to uncover the underlying partition of the arms with the least number of arm pulls and with a probability of error not exceeding a prescribed constant $\delta$. The problem proposed finds numerous applications from clustering of variants of viruses to online market segmentation. We present an instance-dependent information-theoretic lower bound on the expected sample complexity for this task, and design a computationally efficient and asymptotically optimal algorithm, namely Bandit Online Clustering (BOC). The algorithm includes a novel stopping rule for adaptive sequential testing that circumvents the need to exactly solve any NP-hard weighted clustering problem as its subroutines. We show through extensive simulations on synthetic and real-world datasets that BOC's performance matches the lower bound asymptotically, and significantly outperforms a non-adaptive baseline algorithm.

Almost Optimal Variance-Constrained Best Arm Identification

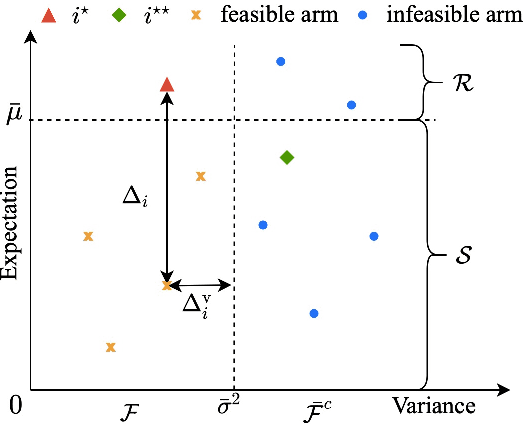
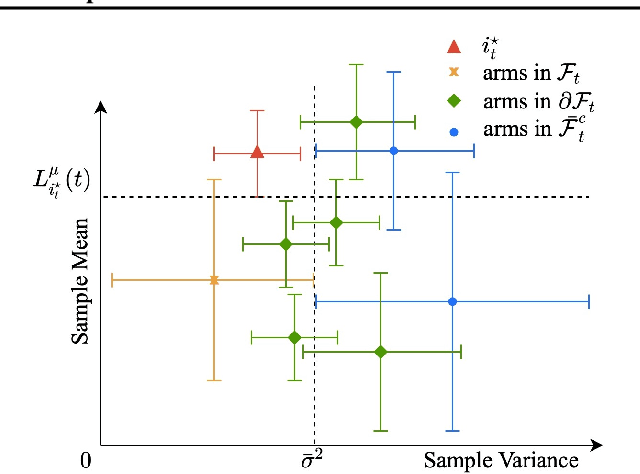
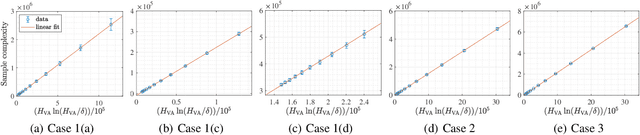
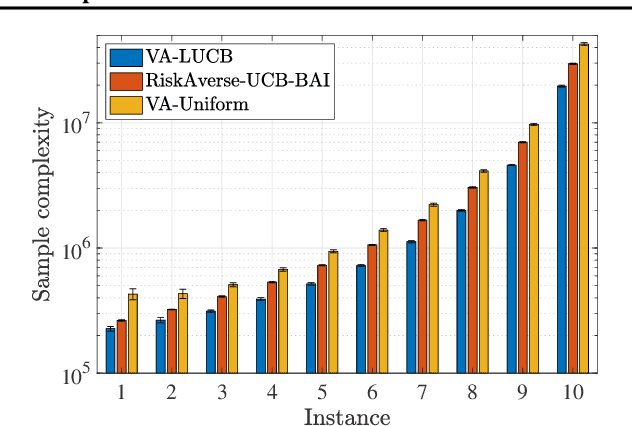
We design and analyze VA-LUCB, a parameter-free algorithm, for identifying the best arm under the fixed-confidence setup and under a stringent constraint that the variance of the chosen arm is strictly smaller than a given threshold. An upper bound on VA-LUCB's sample complexity is shown to be characterized by a fundamental variance-aware hardness quantity $H_{VA}$. By proving a lower bound, we show that sample complexity of VA-LUCB is optimal up to a factor logarithmic in $H_{VA}$. Extensive experiments corroborate the dependence of the sample complexity on the various terms in $H_{VA}$. By comparing VA-LUCB's empirical performance to a close competitor RiskAverse-UCB-BAI by David et al. (2018), our experiments suggest that VA-LUCB has the lowest sample complexity for this class of risk-constrained best arm identification problems, especially for the riskiest instances.

Towards Adversarially Robust Deep Image Denoising

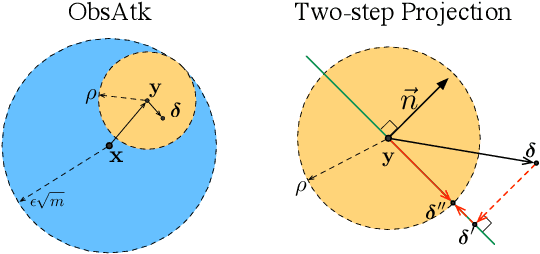
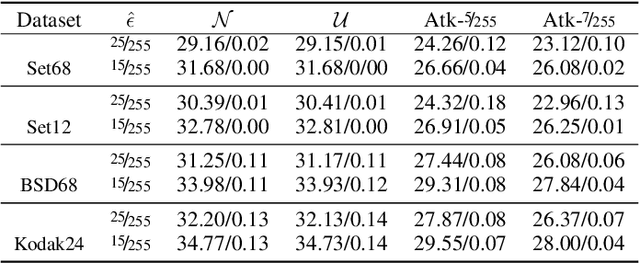
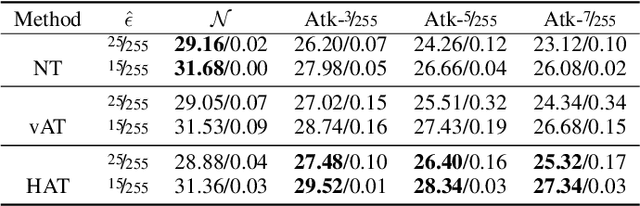
This work systematically investigates the adversarial robustness of deep image denoisers (DIDs), i.e, how well DIDs can recover the ground truth from noisy observations degraded by adversarial perturbations. Firstly, to evaluate DIDs' robustness, we propose a novel adversarial attack, namely Observation-based Zero-mean Attack ({\sc ObsAtk}), to craft adversarial zero-mean perturbations on given noisy images. We find that existing DIDs are vulnerable to the adversarial noise generated by {\sc ObsAtk}. Secondly, to robustify DIDs, we propose an adversarial training strategy, hybrid adversarial training ({\sc HAT}), that jointly trains DIDs with adversarial and non-adversarial noisy data to ensure that the reconstruction quality is high and the denoisers around non-adversarial data are locally smooth. The resultant DIDs can effectively remove various types of synthetic and adversarial noise. We also uncover that the robustness of DIDs benefits their generalization capability on unseen real-world noise. Indeed, {\sc HAT}-trained DIDs can recover high-quality clean images from real-world noise even without training on real noisy data. Extensive experiments on benchmark datasets, including Set68, PolyU, and SIDD, corroborate the effectiveness of {\sc ObsAtk} and {\sc HAT}.

Mimicking the Oracle: An Initial Phase Decorrelation Approach for Class Incremental Learning

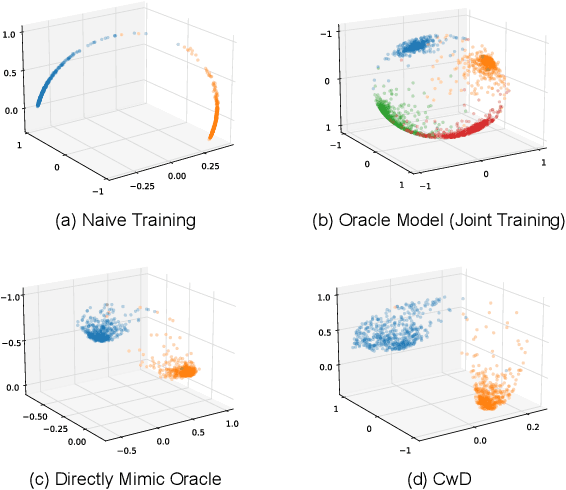
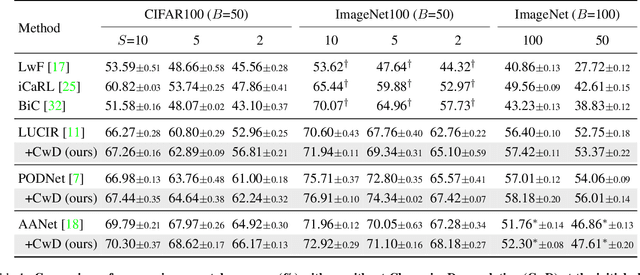
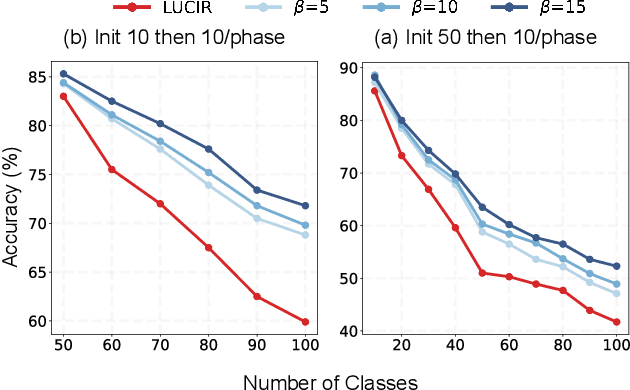
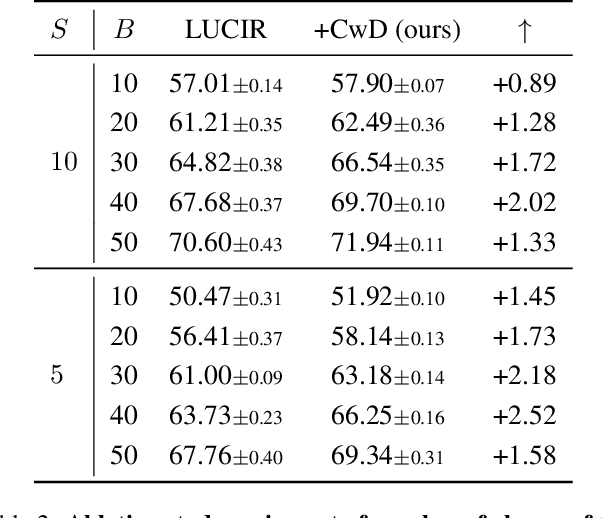
Class Incremental Learning (CIL) aims at learning a multi-class classifier in a phase-by-phase manner, in which only data of a subset of the classes are provided at each phase. Previous works mainly focus on mitigating forgetting in phases after the initial one. However, we find that improving CIL at its initial phase is also a promising direction. Specifically, we experimentally show that directly encouraging CIL Learner at the initial phase to output similar representations as the model jointly trained on all classes can greatly boost the CIL performance. Motivated by this, we study the difference between a na\"ively-trained initial-phase model and the oracle model. Specifically, since one major difference between these two models is the number of training classes, we investigate how such difference affects the model representations. We find that, with fewer training classes, the data representations of each class lie in a long and narrow region; with more training classes, the representations of each class scatter more uniformly. Inspired by this observation, we propose Class-wise Decorrelation (CwD) that effectively regularizes representations of each class to scatter more uniformly, thus mimicking the model jointly trained with all classes (i.e., the oracle model). Our CwD is simple to implement and easy to plug into existing methods. Extensive experiments on various benchmark datasets show that CwD consistently and significantly improves the performance of existing state-of-the-art methods by around 1\% to 3\%. Code will be released.

Active-LATHE: An Active Learning Algorithm for Boosting the Error Exponent for Learning Homogeneous Ising Trees

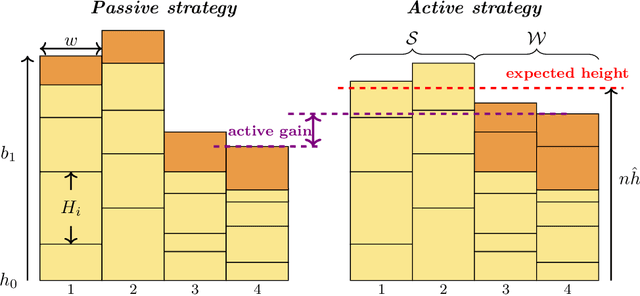
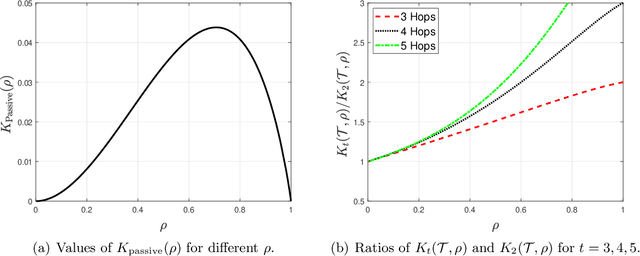
The Chow-Liu algorithm (IEEE Trans.~Inform.~Theory, 1968) has been a mainstay for the learning of tree-structured graphical models from i.i.d.\ sampled data vectors. Its theoretical properties have been well-studied and are well-understood. In this paper, we focus on the class of trees that are arguably even more fundamental, namely {\em homogeneous} trees in which each pair of nodes that forms an edge has the same correlation $\rho$. We ask whether we are able to further reduce the error probability of learning the structure of the homogeneous tree model when {\em active learning} or {\em active sampling of nodes or variables} is allowed. Our figure of merit is the {\em error exponent}, which quantifies the exponential rate of decay of the error probability with an increasing number of data samples. At first sight, an improvement in the error exponent seems impossible, as all the edges are statistically identical. We design and analyze an algorithm Active Learning Algorithm for Trees with Homogeneous Edge (Active-LATHE), which surprisingly boosts the error exponent by at least 40\% when $\rho$ is at least $0.8$. For all other values of $\rho$, we also observe commensurate, but more modest, improvements in the error exponent. Our analysis hinges on judiciously exploiting the minute but detectable statistical variation of the samples to allocate more data to parts of the graph in which we are less confident of being correct.

On the Pareto Frontier of Regret Minimization and Best Arm Identification in Stochastic Bandits

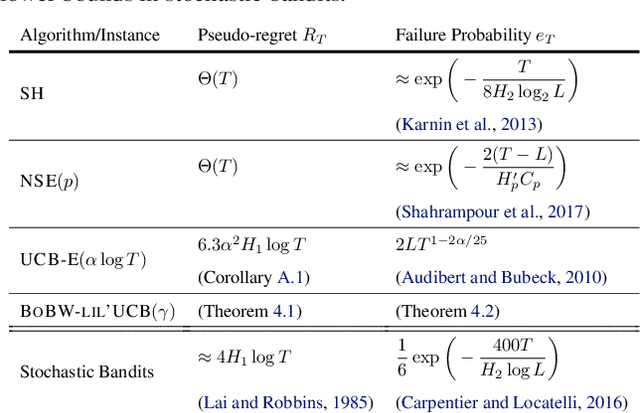
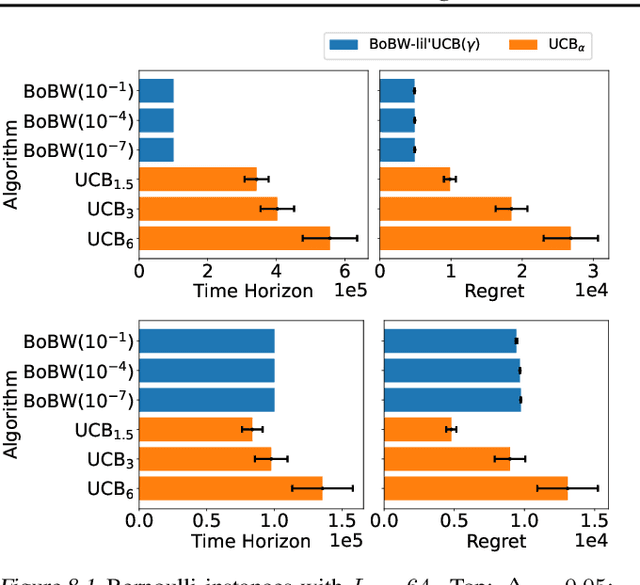
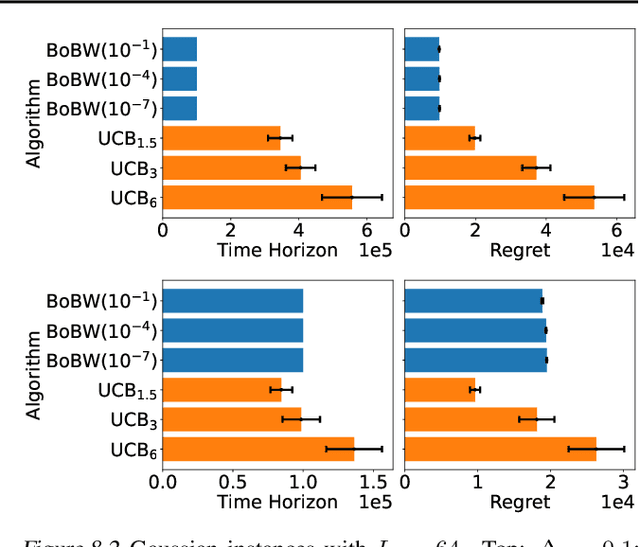
We study the Pareto frontier of two archetypal objectives in stochastic bandits, namely, regret minimization (RM) and best arm identification (BAI) with a fixed horizon. It is folklore that the balance between exploitation and exploration is crucial for both RM and BAI, but exploration is more critical in achieving the optimal performance for the latter objective. To make this precise, we first design and analyze the BoBW-lil'UCB$({\gamma})$ algorithm, which achieves order-wise optimal performance for RM or BAI under different values of ${\gamma}$. Complementarily, we show that no algorithm can simultaneously perform optimally for both the RM and BAI objectives. More precisely, we establish non-trivial lower bounds on the regret achievable by any algorithm with a given BAI failure probability. This analysis shows that in some regimes BoBW-lil'UCB$({\gamma})$ achieves Pareto-optimality up to constant or small terms. Numerical experiments further demonstrate that when applied to difficult instances, BoBW-lil'UCB outperforms a close competitor UCB$_{\alpha}$ (Degenne et al., 2019), which is designed for RM and BAI with a fixed confidence.

Efficient Sharpness-aware Minimization for Improved Training of Neural Networks

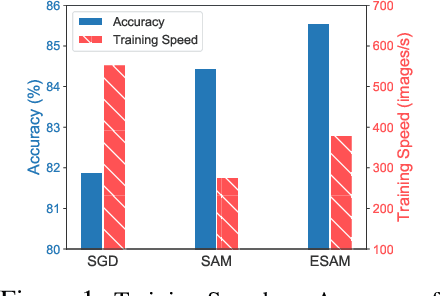
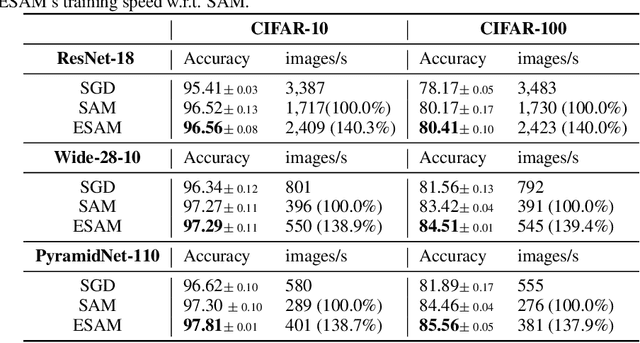
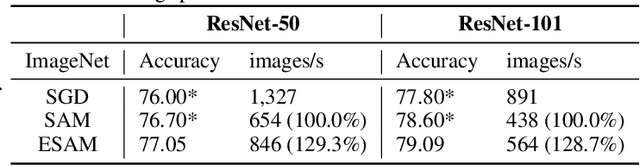
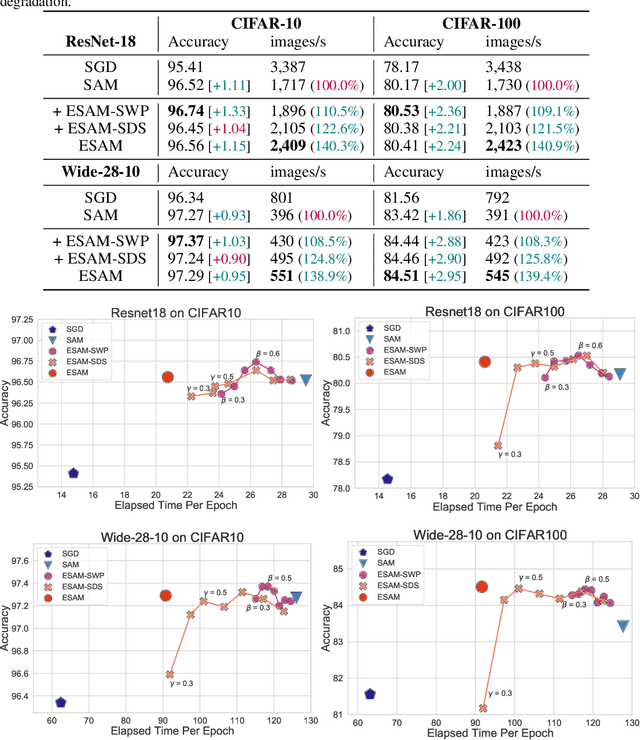
Overparametrized Deep Neural Networks (DNNs) often achieve astounding performances, but may potentially result in severe generalization error. Recently, the relation between the sharpness of the loss landscape and the generalization error has been established by Foret et al. (2020), in which the Sharpness Aware Minimizer (SAM) was proposed to mitigate the degradation of the generalization. Unfortunately, SAM s computational cost is roughly double that of base optimizers, such as Stochastic Gradient Descent (SGD). This paper thus proposes Efficient Sharpness Aware Minimizer (ESAM), which boosts SAM s efficiency at no cost to its generalization performance. ESAM includes two novel and efficient training strategies-StochasticWeight Perturbation and Sharpness-Sensitive Data Selection. In the former, the sharpness measure is approximated by perturbing a stochastically chosen set of weights in each iteration; in the latter, the SAM loss is optimized using only a judiciously selected subset of data that is sensitive to the sharpness. We provide theoretical explanations as to why these strategies perform well. We also show, via extensive experiments on the CIFAR and ImageNet datasets, that ESAM enhances the efficiency over SAM from requiring 100% extra computations to 40% vis-a-vis base optimizers, while test accuracies are preserved or even improved.

Information-Theoretic Generalization Bounds for Iterative Semi-Supervised Learning

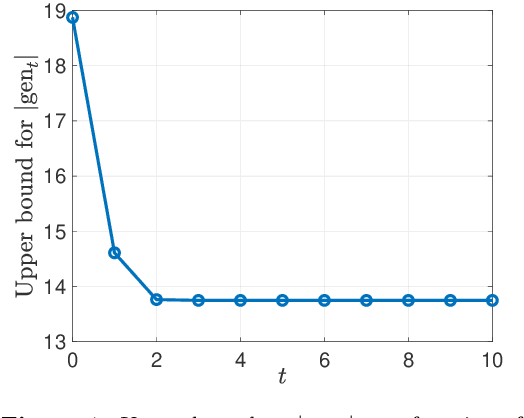
We consider iterative semi-supervised learning (SSL) algorithms that iteratively generate pseudo-labels for a large amount unlabelled data to progressively refine the model parameters. In particular, we seek to understand the behaviour of the {\em generalization error} of iterative SSL algorithms using information-theoretic principles. To obtain bounds that are amenable to numerical evaluation, we first work with a simple model -- namely, the binary Gaussian mixture model. Our theoretical results suggest that when the class conditional variances are not too large, the upper bound on the generalization error decreases monotonically with the number of iterations, but quickly saturates. The theoretical results on the simple model are corroborated by extensive experiments on several benchmark datasets such as the MNIST and CIFAR datasets in which we notice that the generalization error improves after several pseudo-labelling iterations, but saturates afterwards.