Markov Chain Variance Estimation: A Stochastic Approximation Approach

We consider the problem of estimating the asymptotic variance of a function defined on a Markov chain, an important step for statistical inference of the stationary mean. We design the first recursive estimator that requires $O(1)$ computation at each step, does not require storing any historical samples or any prior knowledge of run-length, and has optimal $O(\frac{1}{n})$ rate of convergence for the mean-squared error (MSE) with provable finite sample guarantees. Here, $n$ refers to the total number of samples generated. The previously best-known rate of convergence in MSE was $O(\frac{\log n}{n})$, achieved by jackknifed estimators, which also do not enjoy these other desirable properties. Our estimator is based on linear stochastic approximation of an equivalent formulation of the asymptotic variance in terms of the solution of the Poisson equation. We generalize our estimator in several directions, including estimating the covariance matrix for vector-valued functions, estimating the stationary variance of a Markov chain, and approximately estimating the asymptotic variance in settings where the state space of the underlying Markov chain is large. We also show applications of our estimator in average reward reinforcement learning (RL), where we work with asymptotic variance as a risk measure to model safety-critical applications. We design a temporal-difference type algorithm tailored for policy evaluation in this context. We consider both the tabular and linear function approximation settings. Our work paves the way for developing actor-critic style algorithms for variance-constrained RL.

Optimization of utility-based shortfall risk: A non-asymptotic viewpoint

We consider the problems of estimation and optimization of utility-based shortfall risk (UBSR), which is a popular risk measure in finance. In the context of UBSR estimation, we derive a non-asymptotic bound on the mean-squared error of the classical sample average approximation (SAA) of UBSR. Next, in the context of UBSR optimization, we derive an expression for the UBSR gradient under a smooth parameterization. This expression is a ratio of expectations, both of which involve the UBSR. We use SAA for the numerator as well as denominator in the UBSR gradient expression to arrive at a biased gradient estimator. We derive non-asymptotic bounds on the estimation error, which show that our gradient estimator is asymptotically unbiased. We incorporate the aforementioned gradient estimator into a stochastic gradient (SG) algorithm for UBSR optimization. Finally, we derive non-asymptotic bounds that quantify the rate of convergence of our SG algorithm for UBSR optimization.

VaR\ and CVaR Estimation in a Markov Cost Process: Lower and Upper Bounds

We tackle the problem of estimating the Value-at-Risk (VaR) and the Conditional Value-at-Risk (CVaR) of the infinite-horizon discounted cost within a Markov cost process. First, we derive a minimax lower bound of $\Omega(1/\sqrt{n})$ that holds both in an expected and in a probabilistic sense. Then, using a finite-horizon truncation scheme, we derive an upper bound for the error in CVaR estimation, which matches our lower bound up to constant factors. Finally, we discuss an extension of our estimation scheme that covers more general risk measures satisfying a certain continuity criterion, e.g., spectral risk measures, utility-based shortfall risk. To the best of our knowledge, our work is the first to provide lower and upper bounds on the estimation error for any risk measure within Markovian settings. We remark that our lower bounds also extend to the infinite-horizon discounted costs' mean. Even in that case, our result $\Omega(1/\sqrt{n}) $ improves upon the existing result $\Omega(1/n)$[13].

A Cubic-regularized Policy Newton Algorithm for Reinforcement Learning

We consider the problem of control in the setting of reinforcement learning (RL), where model information is not available. Policy gradient algorithms are a popular solution approach for this problem and are usually shown to converge to a stationary point of the value function. In this paper, we propose two policy Newton algorithms that incorporate cubic regularization. Both algorithms employ the likelihood ratio method to form estimates of the gradient and Hessian of the value function using sample trajectories. The first algorithm requires an exact solution of the cubic regularized problem in each iteration, while the second algorithm employs an efficient gradient descent-based approximation to the cubic regularized problem. We establish convergence of our proposed algorithms to a second-order stationary point (SOSP) of the value function, which results in the avoidance of traps in the form of saddle points. In particular, the sample complexity of our algorithms to find an $\epsilon$-SOSP is $O(\epsilon^{-3.5})$, which is an improvement over the state-of-the-art sample complexity of $O(\epsilon^{-4.5})$.

Finite time analysis of temporal difference learning with linear function approximation: Tail averaging and regularisation

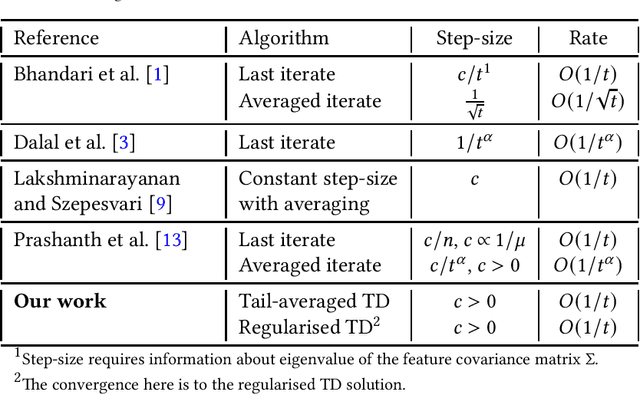
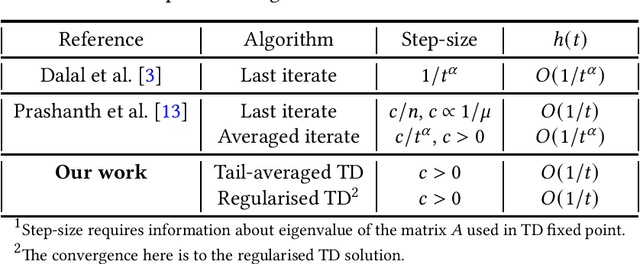
We study the finite-time behaviour of the popular temporal difference (TD) learning algorithm when combined with tail-averaging. We derive finite time bounds on the parameter error of the tail-averaged TD iterate under a step-size choice that does not require information about the eigenvalues of the matrix underlying the projected TD fixed point. Our analysis shows that tail-averaged TD converges at the optimal $O\left(1/t\right)$ rate, both in expectation and with high probability. In addition, our bounds exhibit a sharper rate of decay for the initial error (bias), which is an improvement over averaging all iterates. We also propose and analyse a variant of TD that incorporates regularisation. From analysis, we conclude that the regularised version of TD is useful for problems with ill-conditioned features.

A Gradient Smoothed Functional Algorithm with Truncated Cauchy Random Perturbations for Stochastic Optimization

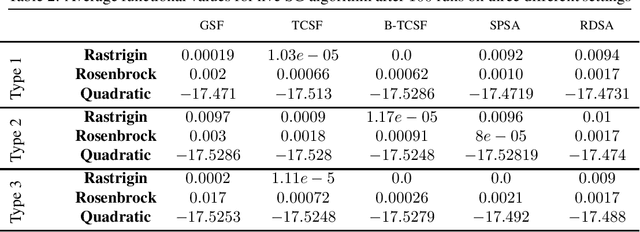
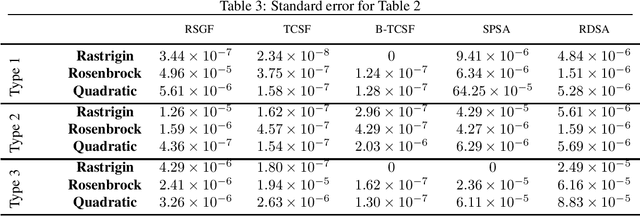
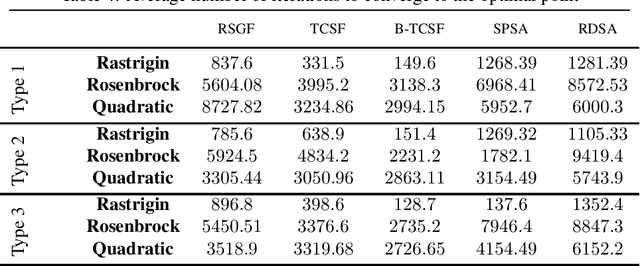
In this paper, we present a stochastic gradient algorithm for minimizing a smooth objective function that is an expectation over noisy cost samples and only the latter are observed for any given parameter. Our algorithm employs a gradient estimation scheme with random perturbations, which are formed using the truncated Cauchy distribution from the unit sphere. We analyze the bias and variance of the proposed gradient estimator. Our algorithm is found to be particularly useful in the case when the objective function is non-convex, and the parameter dimension is high. From an asymptotic convergence analysis, we establish that our algorithm converges almost surely to the set of stationary points of the objective function and obtain the asymptotic convergence rate. We also show that our algorithm avoids unstable equilibria, implying convergence to local minima. Further, we perform a non-asymptotic convergence analysis of our algorithm. In particular, we establish here a non-asymptotic bound for finding an $\epsilon$-stationary point of the non-convex objective function. Finally, we demonstrate numerically through simulations that the performance of our algorithm outperforms GSF, SPSA and RDSA by a significant margin over a few non-convex settings and further validate its performance over convex (noisy) objectives.

A Survey of Risk-Aware Multi-Armed Bandits

In several applications such as clinical trials and financial portfolio optimization, the expected value (or the average reward) does not satisfactorily capture the merits of a drug or a portfolio. In such applications, risk plays a crucial role, and a risk-aware performance measure is preferable, so as to capture losses in the case of adverse events. This survey aims to consolidate and summarise the existing research on risk measures, specifically in the context of multi-armed bandits. We review various risk measures of interest, and comment on their properties. Next, we review existing concentration inequalities for various risk measures. Then, we proceed to defining risk-aware bandit problems, We consider algorithms for the regret minimization setting, where the exploration-exploitation trade-off manifests, as well as the best-arm identification setting, which is a pure exploration problem -- both in the context of risk-sensitive measures. We conclude by commenting on persisting challenges and fertile areas for future research.

Adaptive Estimation of Random Vectors with Bandit Feedback

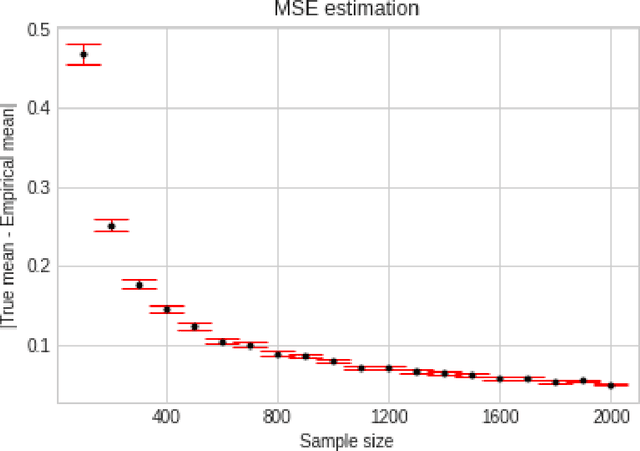
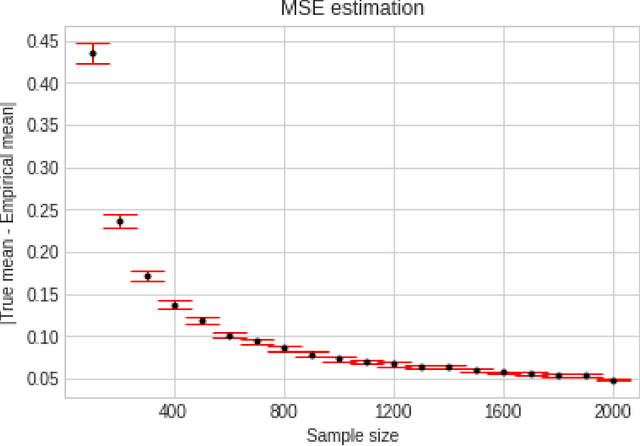
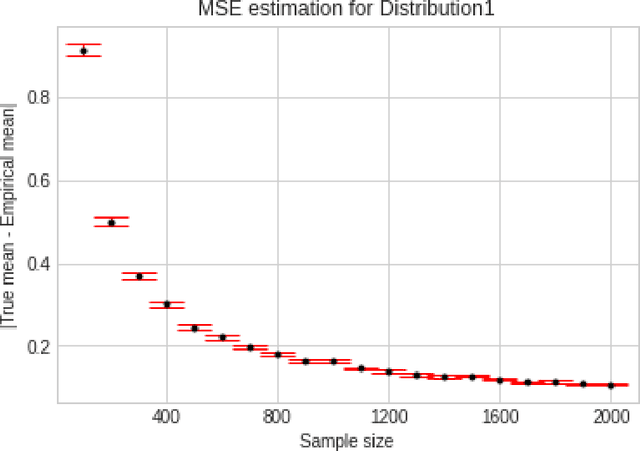
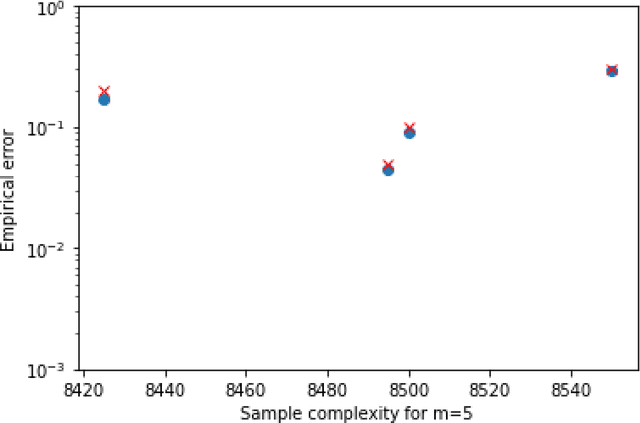
We consider the problem of sequentially learning to estimate, in the mean squared error (MSE) sense, a Gaussian $K$-vector of unknown covariance by observing only $m < K$ of its entries in each round. This reduces to learning an optimal subset for estimating the entire vector. Towards this, we first establish an exponential concentration bound for an estimate of the MSE for each observable subset. We then frame the estimation problem with bandit feedback in the best-subset identification setting. We propose a variant of the successive elimination algorithm to cater to the adaptive estimation problem, and we derive an upper bound on the sample complexity of this algorithm. In addition, to understand the fundamental limit on the sample complexity of this adaptive estimation bandit problem, we derive a minimax lower bound.

Online Estimation and Optimization of Utility-Based Shortfall Risk

Utility-Based Shortfall Risk (UBSR) is a risk metric that is increasingly popular in financial applications, owing to certain desirable properties that it enjoys. We consider the problem of estimating UBSR in a recursive setting, where samples from the underlying loss distribution are available one-at-a-time. We cast the UBSR estimation problem as a root finding problem, and propose stochastic approximation-based estimations schemes. We derive non-asymptotic bounds on the estimation error in the number of samples. We also consider the problem of UBSR optimization within a parameterized class of random variables. We propose a stochastic gradient descent based algorithm for UBSR optimization, and derive non-asymptotic bounds on its convergence.

Estimation of Spectral Risk Measures

We consider the problem of estimating a spectral risk measure (SRM) from i.i.d. samples, and propose a novel method that is based on numerical integration. We show that our SRM estimate concentrates exponentially, when the underlying distribution has bounded support. Further, we also consider the case when the underlying distribution is either Gaussian or exponential, and derive a concentration bound for our estimation scheme. We validate the theoretical findings on a synthetic setup, and in a vehicular traffic routing application.