Refining Labeling Functions with Limited Labeled Data

Programmatic weak supervision (PWS) significantly reduces human effort for labeling data by combining the outputs of user-provided labeling functions (LFs) on unlabeled datapoints. However, the quality of the generated labels depends directly on the accuracy of the LFs. In this work, we study the problem of fixing LFs based on a small set of labeled examples. Towards this goal, we develop novel techniques for repairing a set of LFs by minimally changing their results on the labeled examples such that the fixed LFs ensure that (i) there is sufficient evidence for the correct label of each labeled datapoint and (ii) the accuracy of each repaired LF is sufficiently high. We model LFs as conditional rules which enables us to refine them, i.e., to selectively change their output for some inputs. We demonstrate experimentally that our system improves the quality of LFs based on surprisingly small sets of labeled datapoints.

Graph Neural Network based Double Machine Learning Estimator of Network Causal Effects

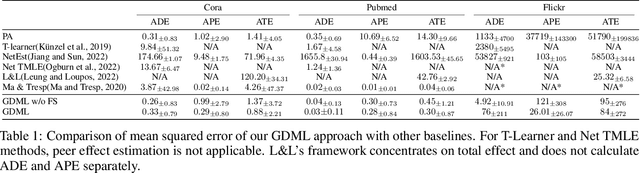
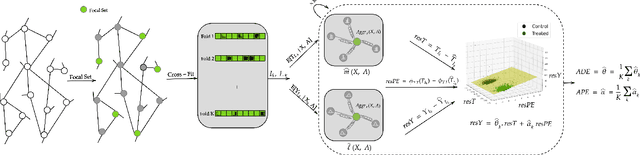
Our paper addresses the challenge of inferring causal effects in social network data, characterized by complex interdependencies among individuals resulting in challenges such as non-independence of units, interference (where a unit's outcome is affected by neighbors' treatments), and introduction of additional confounding factors from neighboring units. We propose a novel methodology combining graph neural networks and double machine learning, enabling accurate and efficient estimation of direct and peer effects using a single observational social network. Our approach utilizes graph isomorphism networks in conjunction with double machine learning to effectively adjust for network confounders and consistently estimate the desired causal effects. We demonstrate that our estimator is both asymptotically normal and semiparametrically efficient. A comprehensive evaluation against four state-of-the-art baseline methods using three semi-synthetic social network datasets reveals our method's on-par or superior efficacy in precise causal effect estimation. Further, we illustrate the practical application of our method through a case study that investigates the impact of Self-Help Group participation on financial risk tolerance. The results indicate a significant positive direct effect, underscoring the potential of our approach in social network analysis. Additionally, we explore the effects of network sparsity on estimation performance.

A Double Machine Learning Approach to Combining Experimental and Observational Data

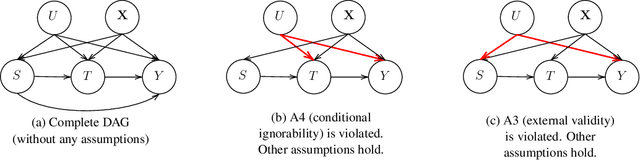
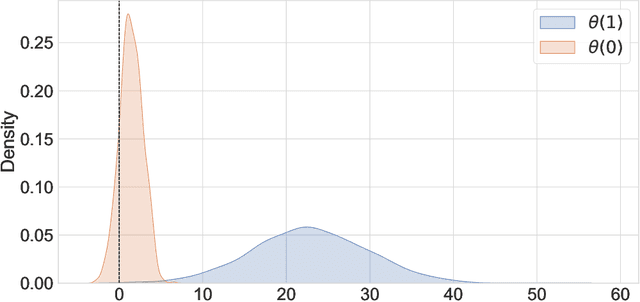
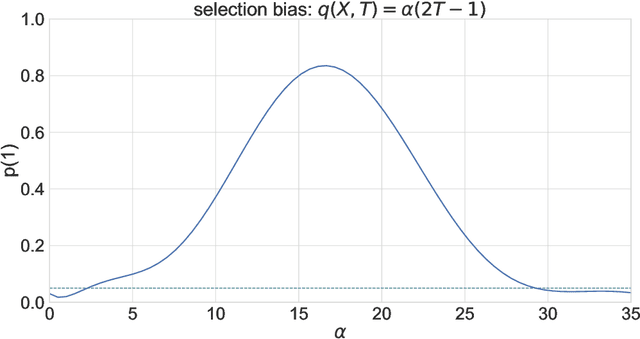
Experimental and observational studies often lack validity due to untestable assumptions. We propose a double machine learning approach to combine experimental and observational studies, allowing practitioners to test for assumption violations and estimate treatment effects consistently. Our framework tests for violations of external validity and ignorability under milder assumptions. When only one assumption is violated, we provide semi-parametrically efficient treatment effect estimators. However, our no-free-lunch theorem highlights the necessity of accurately identifying the violated assumption for consistent treatment effect estimation. We demonstrate the applicability of our approach in three real-world case studies, highlighting its relevance for practical settings.

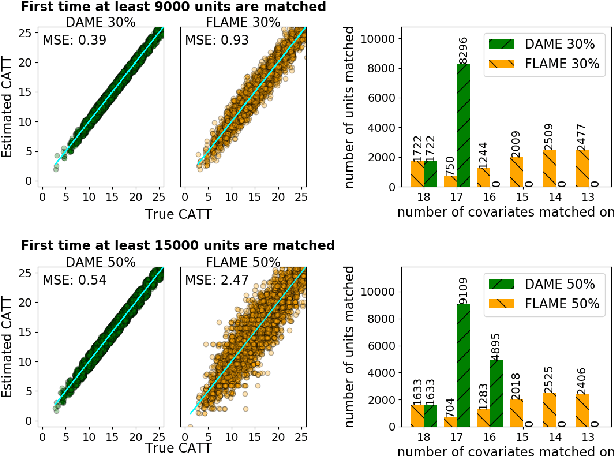
dame-flame: A Python Library Providing Fast Interpretable Matching for Causal Inference

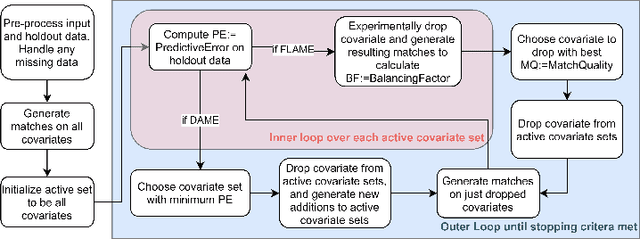
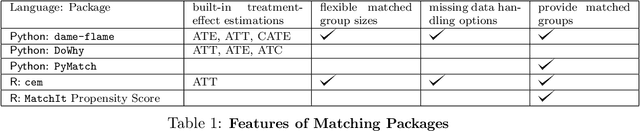
dame-flame is a Python package for performing matching for observational causal inference on datasets containing discrete covariates. This package implements the Dynamic Almost Matching Exactly (DAME) and Fast Large-Scale Almost Matching Exactly (FLAME) algorithms, which match treatment and control units on subsets of the covariates. The resulting matched groups are interpretable, because the matches are made on covariates (rather than, for instance, propensity scores), and high-quality, because machine learning is used to determine which covariates are important to match on. DAME solves an optimization problem that matches units on as many covariates as possible, prioritizing matches on important covariates. FLAME approximates the solution found by DAME via a much faster backward feature selection procedure. The package provides several adjustable parameters to adapt the algorithms to specific applications, and can calculate treatment effects after matching. Descriptions of these parameters, details on estimating treatment effects, and further examples, can be found in the documentation at https://almost-matching-exactly.github.io/DAME-FLAME-Python-Package/

Causal Relational Learning

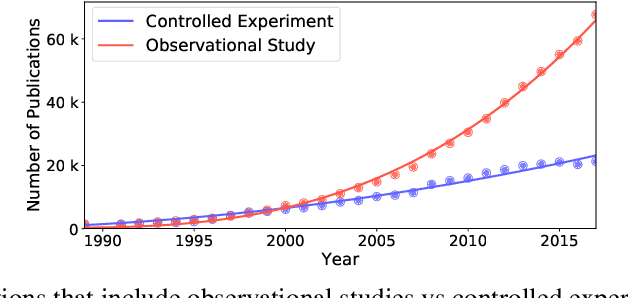
Causal inference is at the heart of empirical research in natural and social sciences and is critical for scientific discovery and informed decision making. The gold standard in causal inference is performing randomized controlled trials; unfortunately these are not always feasible due to ethical, legal, or cost constraints. As an alternative, methodologies for causal inference from observational data have been developed in statistical studies and social sciences. However, existing methods critically rely on restrictive assumptions such as the study population consisting of homogeneous elements that can be represented in a single flat table, where each row is referred to as a unit. In contrast, in many real-world settings, the study domain naturally consists of heterogeneous elements with complex relational structure, where the data is naturally represented in multiple related tables. In this paper, we present a formal framework for causal inference from such relational data. We propose a declarative language called CaRL for capturing causal background knowledge and assumptions and specifying causal queries using simple Datalog-like rules.CaRL provides a foundation for inferring causality and reasoning about the effect of complex interventions in relational domains. We present an extensive experimental evaluation on real relational data to illustrate the applicability of CaRL in social sciences and healthcare.

Adaptive Hyper-box Matching for Interpretable Individualized Treatment Effect Estimation

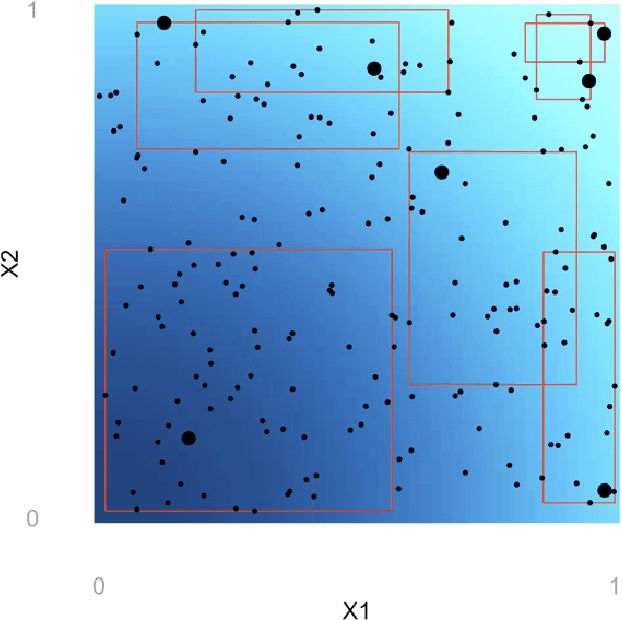
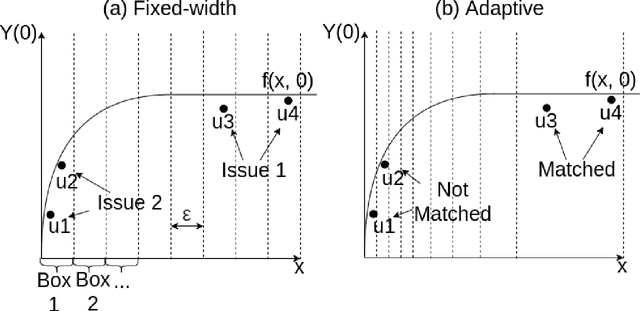
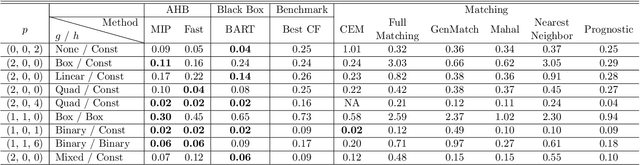
We propose a matching method for observational data that matches units with others in unit-specific, hyper-box-shaped regions of the covariate space. These regions are large enough that many matches are created for each unit and small enough that the treatment effect is roughly constant throughout. The regions are found as either the solution to a mixed integer program, or using a (fast) approximation algorithm. The result is an interpretable and tailored estimate of a causal effect for each unit.

Almost-Matching-Exactly for Treatment Effect Estimation under Network Interference

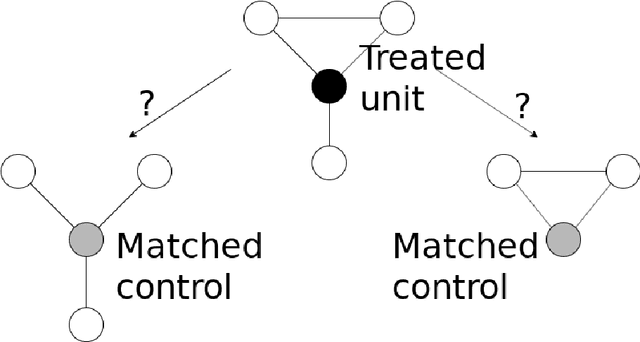
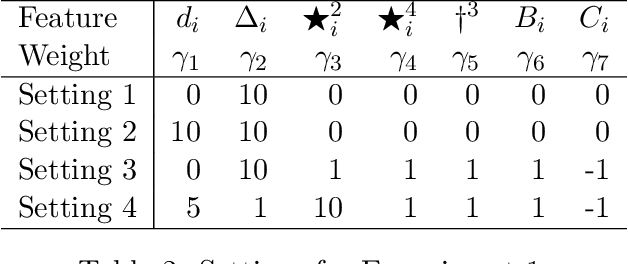
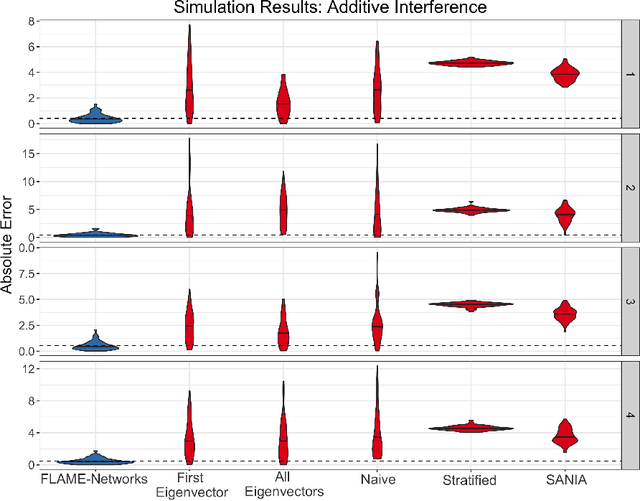
We propose a matching method that recovers direct treatment effects from randomized experiments where units are connected in an observed network, and units that share edges can potentially influence each others' outcomes. Traditional treatment effect estimators for randomized experiments are biased and error prone in this setting. Our method matches units almost exactly on counts of unique subgraphs within their neighborhood graphs. The matches that we construct are interpretable and high-quality. Our method can be extended easily to accommodate additional unit-level covariate information. We show empirically that our method performs better than other existing methodologies for this problem, while producing meaningful, interpretable results.

Interpretable Almost-Matching-Exactly With Instrumental Variables

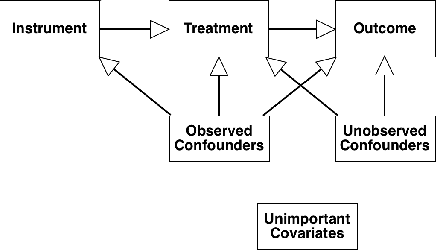
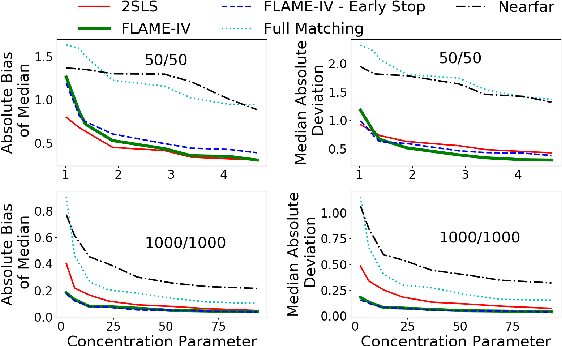
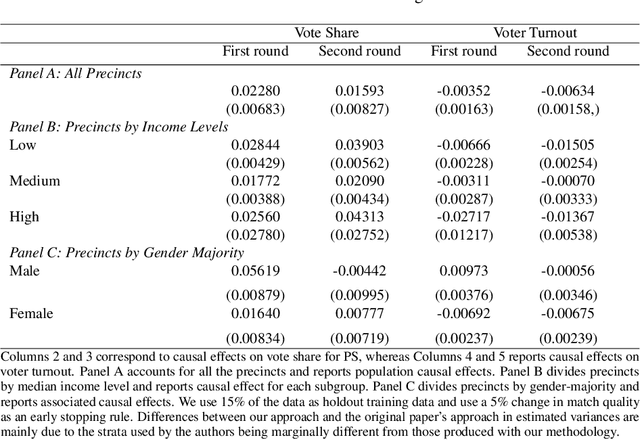
Uncertainty in the estimation of the causal effect in observational studies is often due to unmeasured confounding, i.e., the presence of unobserved covariates linking treatments and outcomes. Instrumental Variables (IV) are commonly used to reduce the effects of unmeasured confounding. Existing methods for IV estimation either require strong parametric assumptions, use arbitrary distance metrics, or do not scale well to large datasets. We propose a matching framework for IV in the presence of observed categorical confounders that addresses these weaknesses. Our method first matches units exactly, and then consecutively drops variables to approximately match the remaining units on as many variables as possible. We show that our algorithm constructs better matches than other existing methods on simulated datasets, and we produce interesting results in an application to political canvassing.

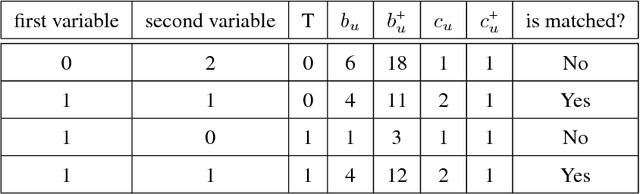
Almost-Exact Matching with Replacement for Causal Inference

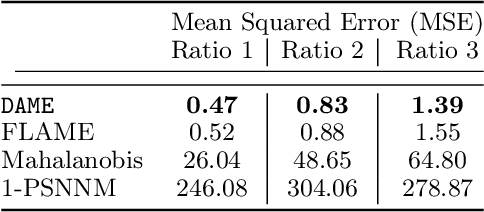
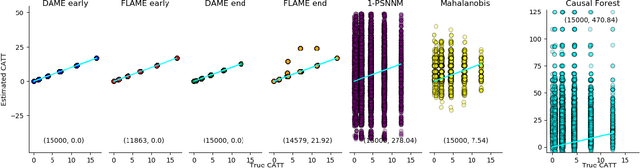
We aim to create the highest possible quality of treatment-control matches for categorical data in the potential outcomes framework. Matching methods are heavily used in the social sciences due to their interpretability, but most matching methods do not pass basic sanity checks: they fail when irrelevant variables are introduced, and tend to be either computationally slow or produce low-quality matches. The method proposed in this work aims to match units on a weighted Hamming distance, taking into account the relative importance of the covariates; the algorithm aims to match units on as many relevant variables as possible. To do this, the algorithm creates a hierarchy of covariate combinations on which to match (similar to downward closure), in the process solving an optimization problem for each unit in order to construct the optimal matches. The algorithm uses a single dynamic program to solve all of the optimization problems simultaneously. Notable advantages of our method over existing matching procedures are its high-quality matches, versatility in handling different data distributions that may have irrelevant variables, and ability to handle missing data by matching on as many available covariates as possible.

FLAME: A Fast Large-scale Almost Matching Exactly Approach to Causal Inference

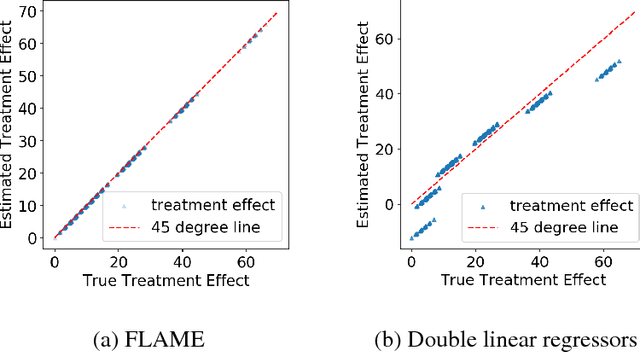
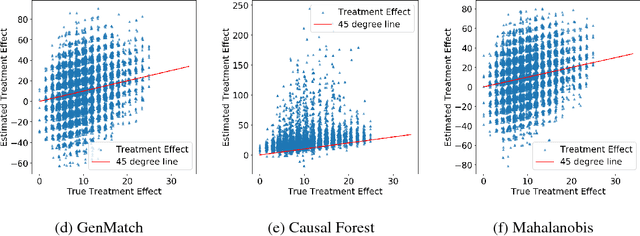
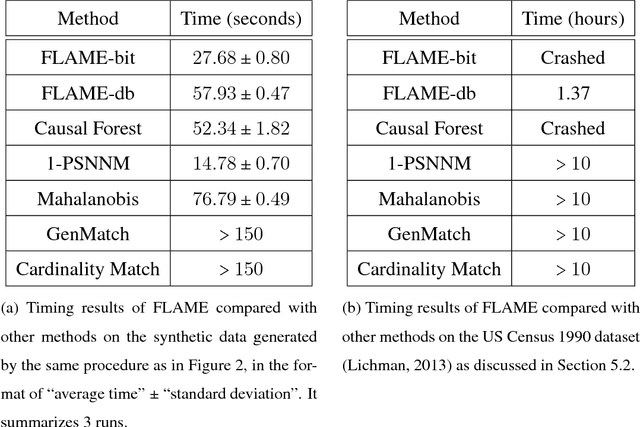
A classical problem in causal inference is that of matching, where treatment units need to be matched to control units. Some of the main challenges in developing matching methods arise from the tension among (i) inclusion of as many covariates as possible in defining the matched groups, (ii) having matched groups with enough treated and control units for a valid estimate of Average Treatment Effect (ATE) in each group, and (iii) computing the matched pairs efficiently for large datasets. In this paper we propose a fast method for approximate and exact matching in causal analysis called FLAME (Fast Large-scale Almost Matching Exactly). We define an optimization objective for match quality, which gives preferences to matching on covariates that can be useful for predicting the outcome while encouraging as many matches as possible. FLAME aims to optimize our match quality measure, leveraging techniques that are natural for query processing in the area of database management. We provide two implementations of FLAME using SQL queries and bit-vector techniques.