Towards Robust Offline Evaluation: A Causal and Information Theoretic Framework for Debiasing Ranking Systems

Evaluating retrieval-ranking systems is crucial for developing high-performing models. While online A/B testing is the gold standard, its high cost and risks to user experience require effective offline methods. However, relying on historical interaction data introduces biases-such as selection, exposure, conformity, and position biases-that distort evaluation metrics, driven by the Missing-Not-At-Random (MNAR) nature of user interactions and favoring popular or frequently exposed items over true user preferences. We propose a novel framework for robust offline evaluation of retrieval-ranking systems, transforming MNAR data into Missing-At-Random (MAR) through reweighting combined with black-box optimization, guided by neural estimation of information-theoretic metrics. Our contributions include (1) a causal formulation for addressing offline evaluation biases, (2) a system-agnostic debiasing framework, and (3) empirical validation of its effectiveness. This framework enables more accurate, fair, and generalizable evaluations, enhancing model assessment before deployment.

Scalable Out-of-distribution Robustness in the Presence of Unobserved Confounders

We consider the task of out-of-distribution (OOD) generalization, where the distribution shift is due to an unobserved confounder ($Z$) affecting both the covariates ($X$) and the labels ($Y$). In this setting, traditional assumptions of covariate and label shift are unsuitable due to the confounding, which introduces heterogeneity in the predictor, i.e., $\hat{Y} = f_Z(X)$. OOD generalization differs from traditional domain adaptation by not assuming access to the covariate distribution ($X^\text{te}$) of the test samples during training. These conditions create a challenging scenario for OOD robustness: (a) $Z^\text{tr}$ is an unobserved confounder during training, (b) $P^\text{te}{Z} \neq P^\text{tr}{Z}$, (c) $X^\text{te}$ is unavailable during training, and (d) the posterior predictive distribution depends on $P^\text{te}(Z)$, i.e., $\hat{Y} = E_{P^\text{te}(Z)}[f_Z(X)]$. In general, accurate predictions are unattainable in this scenario, and existing literature has proposed complex predictors based on identifiability assumptions that require multiple additional variables. Our work investigates a set of identifiability assumptions that tremendously simplify the predictor, whose resulting elegant simplicity outperforms existing approaches.

Graph Neural Network based Double Machine Learning Estimator of Network Causal Effects

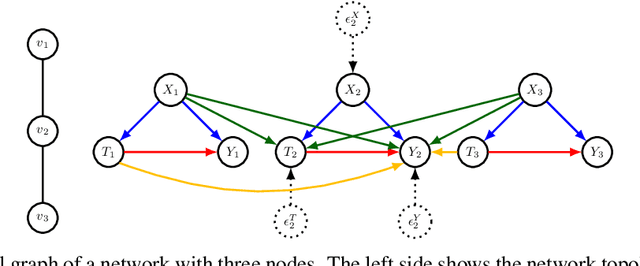
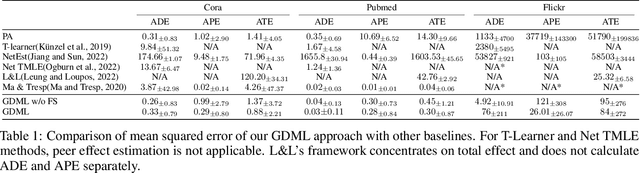
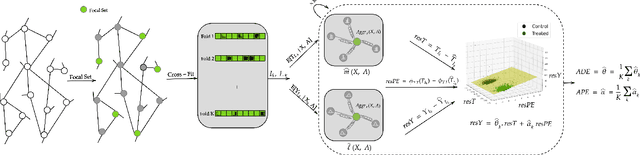
Our paper addresses the challenge of inferring causal effects in social network data, characterized by complex interdependencies among individuals resulting in challenges such as non-independence of units, interference (where a unit's outcome is affected by neighbors' treatments), and introduction of additional confounding factors from neighboring units. We propose a novel methodology combining graph neural networks and double machine learning, enabling accurate and efficient estimation of direct and peer effects using a single observational social network. Our approach utilizes graph isomorphism networks in conjunction with double machine learning to effectively adjust for network confounders and consistently estimate the desired causal effects. We demonstrate that our estimator is both asymptotically normal and semiparametrically efficient. A comprehensive evaluation against four state-of-the-art baseline methods using three semi-synthetic social network datasets reveals our method's on-par or superior efficacy in precise causal effect estimation. Further, we illustrate the practical application of our method through a case study that investigates the impact of Self-Help Group participation on financial risk tolerance. The results indicate a significant positive direct effect, underscoring the potential of our approach in social network analysis. Additionally, we explore the effects of network sparsity on estimation performance.