Data Fusion for Partial Identification of Causal Effects

Data fusion techniques integrate information from heterogeneous data sources to improve learning, generalization, and decision making across data sciences. In causal inference, these methods leverage rich observational data to improve causal effect estimation, while maintaining the trustworthiness of randomized controlled trials. Existing approaches often relax the strong no unobserved confounding assumption by instead assuming exchangeability of counterfactual outcomes across data sources. However, when both assumptions simultaneously fail - a common scenario in practice - current methods cannot identify or estimate causal effects. We address this limitation by proposing a novel partial identification framework that enables researchers to answer key questions such as: Is the causal effect positive or negative? and How severe must assumption violations be to overturn this conclusion? Our approach introduces interpretable sensitivity parameters that quantify assumption violations and derives corresponding causal effect bounds. We develop doubly robust estimators for these bounds and operationalize breakdown frontier analysis to understand how causal conclusions change as assumption violations increase. We apply our framework to the Project STAR study, which investigates the effect of classroom size on students' third-grade standardized test performance. Our analysis reveals that the Project STAR results are robust to simultaneous violations of key assumptions, both on average and across various subgroups of interest. This strengthens confidence in the study's conclusions despite potential unmeasured biases in the data.

A Cautionary Tale on Integrating Studies with Disparate Outcome Measures for Causal Inference

Data integration approaches are increasingly used to enhance the efficiency and generalizability of studies. However, a key limitation of these methods is the assumption that outcome measures are identical across datasets -- an assumption that often does not hold in practice. Consider the following opioid use disorder (OUD) studies: the XBOT trial and the POAT study, both evaluating the effect of medications for OUD on withdrawal symptom severity (not the primary outcome of either trial). While XBOT measures withdrawal severity using the subjective opiate withdrawal scale, POAT uses the clinical opiate withdrawal scale. We analyze this realistic yet challenging setting where outcome measures differ across studies and where neither study records both types of outcomes. Our paper studies whether and when integrating studies with disparate outcome measures leads to efficiency gains. We introduce three sets of assumptions -- with varying degrees of strength -- linking both outcome measures. Our theoretical and empirical results highlight a cautionary tale: integration can improve asymptotic efficiency only under the strongest assumption linking the outcomes. However, misspecification of this assumption leads to bias. In contrast, a milder assumption may yield finite-sample efficiency gains, yet these benefits diminish as sample size increases. We illustrate these trade-offs via a case study integrating the XBOT and POAT datasets to estimate the comparative effect of two medications for opioid use disorder on withdrawal symptoms. By systematically varying the assumptions linking the SOW and COW scales, we show potential efficiency gains and the risks of bias. Our findings emphasize the need for careful assumption selection when fusing datasets with differing outcome measures, offering guidance for researchers navigating this common challenge in modern data integration.

Graph Neural Network based Double Machine Learning Estimator of Network Causal Effects

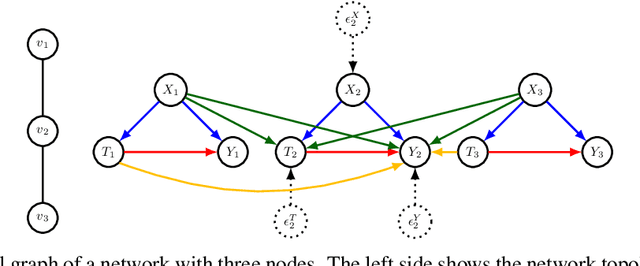
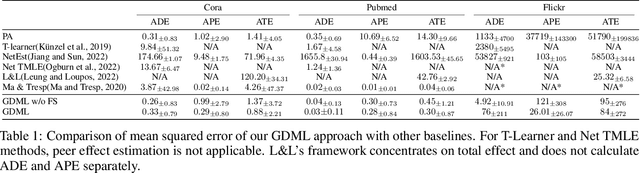
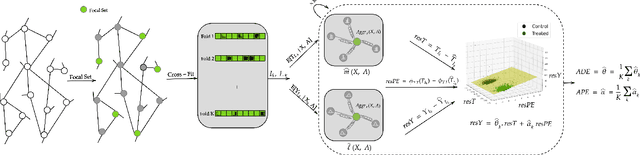
Our paper addresses the challenge of inferring causal effects in social network data, characterized by complex interdependencies among individuals resulting in challenges such as non-independence of units, interference (where a unit's outcome is affected by neighbors' treatments), and introduction of additional confounding factors from neighboring units. We propose a novel methodology combining graph neural networks and double machine learning, enabling accurate and efficient estimation of direct and peer effects using a single observational social network. Our approach utilizes graph isomorphism networks in conjunction with double machine learning to effectively adjust for network confounders and consistently estimate the desired causal effects. We demonstrate that our estimator is both asymptotically normal and semiparametrically efficient. A comprehensive evaluation against four state-of-the-art baseline methods using three semi-synthetic social network datasets reveals our method's on-par or superior efficacy in precise causal effect estimation. Further, we illustrate the practical application of our method through a case study that investigates the impact of Self-Help Group participation on financial risk tolerance. The results indicate a significant positive direct effect, underscoring the potential of our approach in social network analysis. Additionally, we explore the effects of network sparsity on estimation performance.

Towards Generalizing Inferences from Trials to Target Populations

Randomized Controlled Trials (RCTs) are pivotal in generating internally valid estimates with minimal assumptions, serving as a cornerstone for researchers dedicated to advancing causal inference methods. However, extending these findings beyond the experimental cohort to achieve externally valid estimates is crucial for broader scientific inquiry. This paper delves into the forefront of addressing these external validity challenges, encapsulating the essence of a multidisciplinary workshop held at the Institute for Computational and Experimental Research in Mathematics (ICERM), Brown University, in Fall 2023. The workshop congregated experts from diverse fields including social science, medicine, public health, statistics, computer science, and education, to tackle the unique obstacles each discipline faces in extrapolating experimental findings. Our study presents three key contributions: we integrate ongoing efforts, highlighting methodological synergies across fields; provide an exhaustive review of generalizability and transportability based on the workshop's discourse; and identify persistent hurdles while suggesting avenues for future research. By doing so, this paper aims to enhance the collective understanding of the generalizability and transportability of causal effects, fostering cross-disciplinary collaboration and offering valuable insights for researchers working on refining and applying causal inference methods.

Who Are We Missing? A Principled Approach to Characterizing the Underrepresented Population

Randomized controlled trials (RCTs) serve as the cornerstone for understanding causal effects, yet extending inferences to target populations presents challenges due to effect heterogeneity and underrepresentation. Our paper addresses the critical issue of identifying and characterizing underrepresented subgroups in RCTs, proposing a novel framework for refining target populations to improve generalizability. We introduce an optimization-based approach, Rashomon Set of Optimal Trees (ROOT), to characterize underrepresented groups. ROOT optimizes the target subpopulation distribution by minimizing the variance of the target average treatment effect estimate, ensuring more precise treatment effect estimations. Notably, ROOT generates interpretable characteristics of the underrepresented population, aiding researchers in effective communication. Our approach demonstrates improved precision and interpretability compared to alternatives, as illustrated with synthetic data experiments. We apply our methodology to extend inferences from the Starting Treatment with Agonist Replacement Therapies (START) trial -- investigating the effectiveness of medication for opioid use disorder -- to the real-world population represented by the Treatment Episode Dataset: Admissions (TEDS-A). By refining target populations using ROOT, our framework offers a systematic approach to enhance decision-making accuracy and inform future trials in diverse populations.

Interpretable Causal Inference for Analyzing Wearable, Sensor, and Distributional Data

Many modern causal questions ask how treatments affect complex outcomes that are measured using wearable devices and sensors. Current analysis approaches require summarizing these data into scalar statistics (e.g., the mean), but these summaries can be misleading. For example, disparate distributions can have the same means, variances, and other statistics. Researchers can overcome the loss of information by instead representing the data as distributions. We develop an interpretable method for distributional data analysis that ensures trustworthy and robust decision-making: Analyzing Distributional Data via Matching After Learning to Stretch (ADD MALTS). We (i) provide analytical guarantees of the correctness of our estimation strategy, (ii) demonstrate via simulation that ADD MALTS outperforms other distributional data analysis methods at estimating treatment effects, and (iii) illustrate ADD MALTS' ability to verify whether there is enough cohesion between treatment and control units within subpopulations to trustworthily estimate treatment effects. We demonstrate ADD MALTS' utility by studying the effectiveness of continuous glucose monitors in mitigating diabetes risks.

Estimating Trustworthy and Safe Optimal Treatment Regimes

Recent statistical and reinforcement learning methods have significantly advanced patient care strategies. However, these approaches face substantial challenges in high-stakes contexts, including missing data, inherent stochasticity, and the critical requirements for interpretability and patient safety. Our work operationalizes a safe and interpretable framework to identify optimal treatment regimes. This approach involves matching patients with similar medical and pharmacological characteristics, allowing us to construct an optimal policy via interpolation. We perform a comprehensive simulation study to demonstrate the framework's ability to identify optimal policies even in complex settings. Ultimately, we operationalize our approach to study regimes for treating seizures in critically ill patients. Our findings strongly support personalized treatment strategies based on a patient's medical history and pharmacological features. Notably, we identify that reducing medication doses for patients with mild and brief seizure episodes while adopting aggressive treatment for patients in intensive care unit experiencing intense seizures leads to more favorable outcomes.

A Double Machine Learning Approach to Combining Experimental and Observational Data

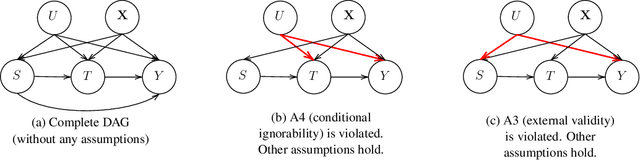
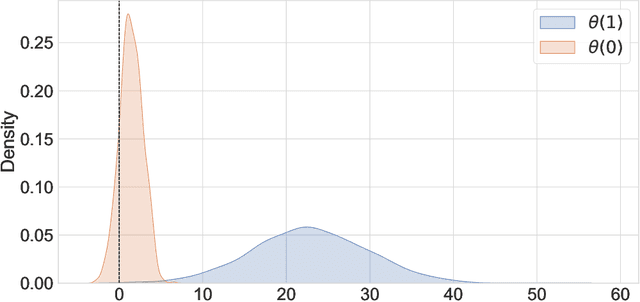
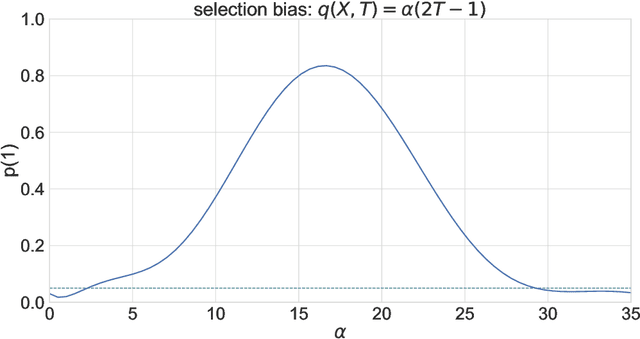
Experimental and observational studies often lack validity due to untestable assumptions. We propose a double machine learning approach to combine experimental and observational studies, allowing practitioners to test for assumption violations and estimate treatment effects consistently. Our framework tests for violations of external validity and ignorability under milder assumptions. When only one assumption is violated, we provide semi-parametrically efficient treatment effect estimators. However, our no-free-lunch theorem highlights the necessity of accurately identifying the violated assumption for consistent treatment effect estimation. We demonstrate the applicability of our approach in three real-world case studies, highlighting its relevance for practical settings.

From Feature Importance to Distance Metric: An Almost Exact Matching Approach for Causal Inference

Our goal is to produce methods for observational causal inference that are auditable, easy to troubleshoot, yield accurate treatment effect estimates, and scalable to high-dimensional data. We describe an almost-exact matching approach that achieves these goals by (i) learning a distance metric via outcome modeling, (ii) creating matched groups using the distance metric, and (iii) using the matched groups to estimate treatment effects. Our proposed method uses variable importance measurements to construct a distance metric, making it a flexible method that can be adapted to various applications. Concentrating on the scalability of the problem in the number of potential confounders, we operationalize our approach with LASSO. We derive performance guarantees for settings where LASSO outcome modeling consistently identifies all confounders (importantly without requiring the linear model to be correctly specified). We also provide experimental results demonstrating the auditability of matches, as well as extensions to more general nonparametric outcome modeling.

Are Synthetic Control Weights Balancing Score?

In this short note, I outline conditions under which conditioning on Synthetic Control (SC) weights emulates a randomized control trial where the treatment status is independent of potential outcomes. Specifically, I demonstrate that if there exist SC weights such that (i) the treatment effects are exactly identified and (ii) these weights are uniformly and cumulatively bounded, then SC weights are balancing scores.