Talk2Move: Reinforcement Learning for Text-Instructed Object-Level Geometric Transformation in Scenes

We introduce Talk2Move, a reinforcement learning (RL) based diffusion framework for text-instructed spatial transformation of objects within scenes. Spatially manipulating objects in a scene through natural language poses a challenge for multimodal generation systems. While existing text-based manipulation methods can adjust appearance or style, they struggle to perform object-level geometric transformations-such as translating, rotating, or resizing objects-due to scarce paired supervision and pixel-level optimization limits. Talk2Move employs Group Relative Policy Optimization (GRPO) to explore geometric actions through diverse rollouts generated from input images and lightweight textual variations, removing the need for costly paired data. A spatial reward guided model aligns geometric transformations with linguistic description, while off-policy step evaluation and active step sampling improve learning efficiency by focusing on informative transformation stages. Furthermore, we design object-centric spatial rewards that evaluate displacement, rotation, and scaling behaviors directly, enabling interpretable and coherent transformations. Experiments on curated benchmarks demonstrate that Talk2Move achieves precise, consistent, and semantically faithful object transformations, outperforming existing text-guided editing approaches in both spatial accuracy and scene coherence.

Experience-Guided Adaptation of Inference-Time Reasoning Strategies

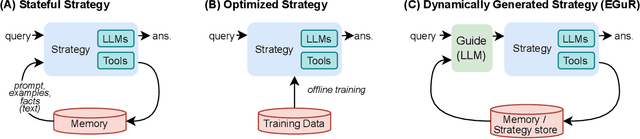
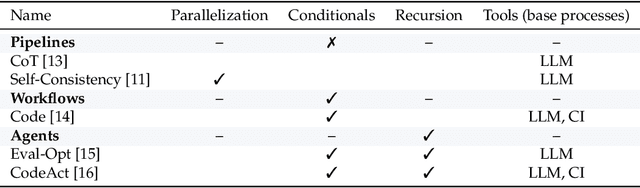
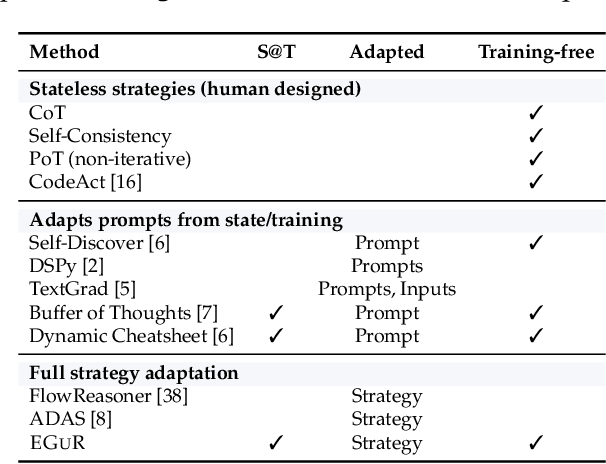
Enabling agentic AI systems to adapt their problem-solving approaches based on post-training interactions remains a fundamental challenge. While systems that update and maintain a memory at inference time have been proposed, existing designs only steer the system by modifying textual input to a language model or agent, which means that they cannot change sampling parameters, remove tools, modify system prompts, or switch between agentic and workflow paradigms. On the other hand, systems that adapt more flexibly require offline optimization and remain static once deployed. We present Experience-Guided Reasoner (EGuR), which generates tailored strategies -- complete computational procedures involving LLM calls, tools, sampling parameters, and control logic -- dynamically at inference time based on accumulated experience. We achieve this using an LLM-based meta-strategy -- a strategy that outputs strategies -- enabling adaptation of all strategy components (prompts, sampling parameters, tool configurations, and control logic). EGuR operates through two components: a Guide generates multiple candidate strategies conditioned on the current problem and structured memory of past experiences, while a Consolidator integrates execution feedback to improve future strategy generation. This produces complete, ready-to-run strategies optimized for each problem, which can be cached, retrieved, and executed as needed without wasting resources. Across five challenging benchmarks (AIME 2025, 3-SAT, and three Big Bench Extra Hard tasks), EGuR achieves up to 14% accuracy improvements over the strongest baselines while reducing computational costs by up to 111x, with both metrics improving as the system gains experience.

MURPHY: Multi-Turn GRPO for Self Correcting Code Generation

Reinforcement Learning with Verifiable Rewards (RLVR) has emerged as a powerful framework for enhancing the reasoning capabilities of large language models (LLMs). However, existing approaches such as Group Relative Policy Optimization (GRPO) and its variants, while effective on reasoning benchmarks, struggle with agentic tasks that require iterative decision-making. We introduce Murphy, a multi-turn reflective optimization framework that extends GRPO by incorporating iterative self-correction during training. By leveraging both quantitative and qualitative execution feedback, Murphy enables models to progressively refine their reasoning across multiple turns. Evaluations on code generation benchmarks with model families such as Qwen and OLMo show that Murphy consistently improves performance, achieving up to a 8% relative gain in pass@1 over GRPO, on similar compute budgets.

Learning to Focus: Focal Attention for Selective and Scalable Transformers

Attention is a core component of transformer architecture, whether encoder-only, decoder-only, or encoder-decoder model. However, the standard softmax attention often produces noisy probability distribution, which can impair effective feature selection at every layer of these models, particularly for long contexts. We propose Focal Attention, a simple yet effective modification that sharpens the attention distribution by controlling the softmax temperature, either as a fixed hyperparameter or as a learnable parameter during training. This sharpening enables the model to concentrate on the most relevant tokens while suppressing irrelevant ones. Empirically, Focal Attention scales more favorably than standard transformer with respect to model size, training data, and context length. Across diverse benchmarks, it achieves the same accuracy with up to 42% fewer parameters or 33% less training data. On long-context tasks, it delivers substantial relative improvements ranging from 17% to 82%, demonstrating its effectiveness in real world applications.

e1: Learning Adaptive Control of Reasoning Effort

Increasing the thinking budget of AI models can significantly improve accuracy, but not all questions warrant the same amount of reasoning. Users may prefer to allocate different amounts of reasoning effort depending on how they value output quality versus latency and cost. To leverage this tradeoff effectively, users need fine-grained control over the amount of thinking used for a particular query, but few approaches enable such control. Existing methods require users to specify the absolute number of desired tokens, but this requires knowing the difficulty of the problem beforehand to appropriately set the token budget for a query. To address these issues, we propose Adaptive Effort Control, a self-adaptive reinforcement learning method that trains models to use a user-specified fraction of tokens relative to the current average chain-of-thought length for each query. This approach eliminates dataset- and phase-specific tuning while producing better cost-accuracy tradeoff curves compared to standard methods. Users can dynamically adjust the cost-accuracy trade-off through a continuous effort parameter specified at inference time. We observe that the model automatically learns to allocate resources proportionally to the task difficulty and, across model scales ranging from 1.5B to 32B parameters, our approach enables approximately 3x reduction in chain-of-thought length while maintaining or improving performance relative to the base model used for RL training.

Maximally-Informative Retrieval for State Space Model Generation

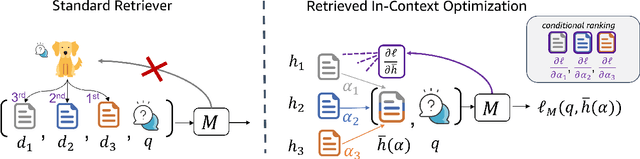
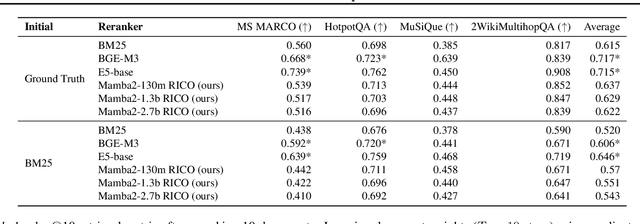
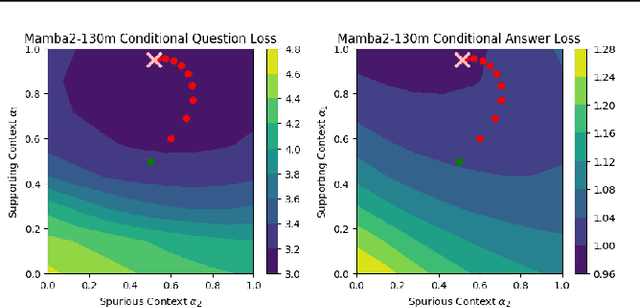
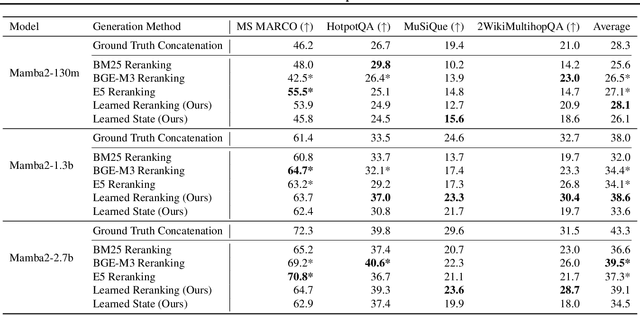
Given a query and dataset, the optimal way of answering the query is to make use all the information available. Modern LLMs exhibit impressive ability to memorize training data, but data not deemed important during training is forgotten, and information outside that training set cannot be made use of. Processing an entire dataset at inference time is infeasible due to the bounded nature of model resources (e.g. context size in transformers or states in state space models), meaning we must resort to external memory. This constraint naturally leads to the following problem: How can we decide based on the present query and model, what among a virtually unbounded set of known data matters for inference? To minimize model uncertainty for a particular query at test-time, we introduce Retrieval In-Context Optimization (RICO), a retrieval method that uses gradients from the LLM itself to learn the optimal mixture of documents for answer generation. Unlike traditional retrieval-augmented generation (RAG), which relies on external heuristics for document retrieval, our approach leverages direct feedback from the model. Theoretically, we show that standard top-$k$ retrieval with model gradients can approximate our optimization procedure, and provide connections to the leave-one-out loss. We demonstrate empirically that by minimizing an unsupervised loss objective in the form of question perplexity, we can achieve comparable retriever metric performance to BM25 with \emph{no finetuning}. Furthermore, when evaluated on quality of the final prediction, our method often outperforms fine-tuned dense retrievers such as E5.

STree: Speculative Tree Decoding for Hybrid State-Space Models

Speculative decoding is a technique to leverage hardware concurrency to improve the efficiency of large-scale autoregressive (AR) Transformer models by enabling multiple steps of token generation in a single forward pass. State-space models (SSMs) are already more efficient than AR Transformers, since their state summarizes all past data with no need to cache or re-process tokens in the sliding window context. However, their state can also comprise thousands of tokens; so, speculative decoding has recently been extended to SSMs. Existing approaches, however, do not leverage the tree-based verification methods, since current SSMs lack the means to compute a token tree efficiently. We propose the first scalable algorithm to perform tree-based speculative decoding in state-space models (SSMs) and hybrid architectures of SSMs and Transformer layers. We exploit the structure of accumulated state transition matrices to facilitate tree-based speculative decoding with minimal overhead to current SSM state update implementations. With the algorithm, we describe a hardware-aware implementation that improves naive application of AR Transformer tree-based speculative decoding methods to SSMs. Furthermore, we outperform vanilla speculative decoding with SSMs even with a baseline drafting model and tree structure on three different benchmarks, opening up opportunities for further speed up with SSM and hybrid model inference. Code will be released upon paper acceptance.

Robust Planning for Autonomous Driving via Mixed Adversarial Diffusion Predictions

We describe a robust planning method for autonomous driving that mixes normal and adversarial agent predictions output by a diffusion model trained for motion prediction. We first train a diffusion model to learn an unbiased distribution of normal agent behaviors. We then generate a distribution of adversarial predictions by biasing the diffusion model at test time to generate predictions that are likely to collide with a candidate plan. We score plans using expected cost with respect to a mixture distribution of normal and adversarial predictions, leading to a planner that is robust against adversarial behaviors but not overly conservative when agents behave normally. Unlike current approaches, we do not use risk measures that over-weight adversarial behaviors while placing little to no weight on low-cost normal behaviors or use hard safety constraints that may not be appropriate for all driving scenarios. We show the effectiveness of our method on single-agent and multi-agent jaywalking scenarios as well as a red light violation scenario.

PICASO: Permutation-Invariant Context Composition with State Space Models

Providing Large Language Models with relevant contextual knowledge at inference time has been shown to greatly improve the quality of their generations. This is often achieved by prepending informative passages of text, or 'contexts', retrieved from external knowledge bases to their input. However, processing additional contexts online incurs significant computation costs that scale with their length. State Space Models (SSMs) offer a promising solution by allowing a database of contexts to be mapped onto fixed-dimensional states from which to start the generation. A key challenge arises when attempting to leverage information present across multiple contexts, since there is no straightforward way to condition generation on multiple independent states in existing SSMs. To address this, we leverage a simple mathematical relation derived from SSM dynamics to compose multiple states into one that efficiently approximates the effect of concatenating textual contexts. Since the temporal ordering of contexts can often be uninformative, we enforce permutation-invariance by efficiently averaging states obtained via our composition algorithm across all possible context orderings. We evaluate our resulting method on WikiText and MSMARCO in both zero-shot and fine-tuned settings, and show that we can match the strongest performing baseline while enjoying on average 5.4x speedup.

Descriminative-Generative Custom Tokens for Vision-Language Models

This paper explores the possibility of learning custom tokens for representing new concepts in Vision-Language Models (VLMs). Our aim is to learn tokens that can be effective for both discriminative and generative tasks while composing well with words to form new input queries. The targeted concept is specified in terms of a small set of images and a parent concept described using text. We operate on CLIP text features and propose to use a combination of a textual inversion loss and a classification loss to ensure that text features of the learned token are aligned with image features of the concept in the CLIP embedding space. We restrict the learned token to a low-dimensional subspace spanned by tokens for attributes that are appropriate for the given super-class. These modifications improve the quality of compositions of the learned token with natural language for generating new scenes. Further, we show that learned custom tokens can be used to form queries for text-to-image retrieval task, and also have the important benefit that composite queries can be visualized to ensure that the desired concept is faithfully encoded. Based on this, we introduce the method of Generation Aided Image Retrieval, where the query is modified at inference time to better suit the search intent. On the DeepFashion2 dataset, our method improves Mean Reciprocal Retrieval (MRR) over relevant baselines by 7%.