Matthew Trager
UCLA-CS
Evolutionary Generation of Multi-Agent Systems
Feb 06, 2026Abstract:Large language model (LLM)-based multi-agent systems (MAS) show strong promise for complex reasoning, planning, and tool-augmented tasks, but designing effective MAS architectures remains labor-intensive, brittle, and hard to generalize. Existing automatic MAS generation methods either rely on code generation, which often leads to executability and robustness failures, or impose rigid architectural templates that limit expressiveness and adaptability. We propose Evolutionary Generation of Multi-Agent Systems (EvoMAS), which formulates MAS generation as structured configuration generation. EvoMAS performs evolutionary generation in configuration space. Specifically, EvoMAS selects initial configurations from a pool, applies feedback-conditioned mutation and crossover guided by execution traces, and iteratively refines both the candidate pool and an experience memory. We evaluate EvoMAS on diverse benchmarks, including BBEH, SWE-Bench, and WorkBench, covering reasoning, software engineering, and tool-use tasks. EvoMAS consistently improves task performance over both human-designed MAS and prior automatic MAS generation methods, while producing generated systems with higher executability and runtime robustness. EvoMAS outperforms the agent evolution method EvoAgent by +10.5 points on BBEH reasoning and +7.1 points on WorkBench. With Claude-4.5-Sonnet, EvoMAS also reaches 79.1% on SWE-Bench-Verified, matching the top of the leaderboard.
Experience-Guided Adaptation of Inference-Time Reasoning Strategies
Nov 14, 2025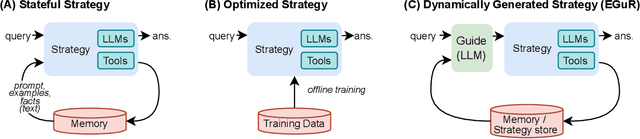
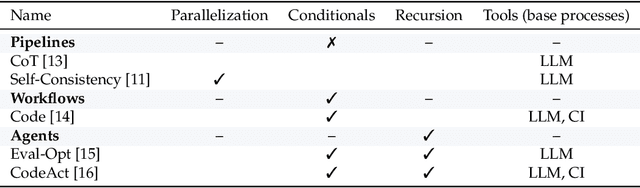

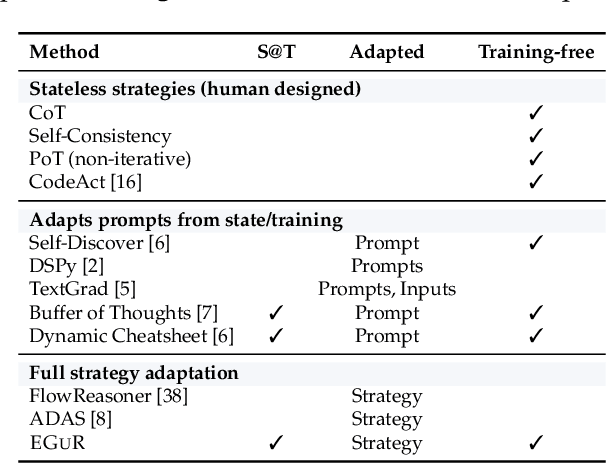
Abstract:Enabling agentic AI systems to adapt their problem-solving approaches based on post-training interactions remains a fundamental challenge. While systems that update and maintain a memory at inference time have been proposed, existing designs only steer the system by modifying textual input to a language model or agent, which means that they cannot change sampling parameters, remove tools, modify system prompts, or switch between agentic and workflow paradigms. On the other hand, systems that adapt more flexibly require offline optimization and remain static once deployed. We present Experience-Guided Reasoner (EGuR), which generates tailored strategies -- complete computational procedures involving LLM calls, tools, sampling parameters, and control logic -- dynamically at inference time based on accumulated experience. We achieve this using an LLM-based meta-strategy -- a strategy that outputs strategies -- enabling adaptation of all strategy components (prompts, sampling parameters, tool configurations, and control logic). EGuR operates through two components: a Guide generates multiple candidate strategies conditioned on the current problem and structured memory of past experiences, while a Consolidator integrates execution feedback to improve future strategy generation. This produces complete, ready-to-run strategies optimized for each problem, which can be cached, retrieved, and executed as needed without wasting resources. Across five challenging benchmarks (AIME 2025, 3-SAT, and three Big Bench Extra Hard tasks), EGuR achieves up to 14% accuracy improvements over the strongest baselines while reducing computational costs by up to 111x, with both metrics improving as the system gains experience.
e1: Learning Adaptive Control of Reasoning Effort
Oct 30, 2025Abstract:Increasing the thinking budget of AI models can significantly improve accuracy, but not all questions warrant the same amount of reasoning. Users may prefer to allocate different amounts of reasoning effort depending on how they value output quality versus latency and cost. To leverage this tradeoff effectively, users need fine-grained control over the amount of thinking used for a particular query, but few approaches enable such control. Existing methods require users to specify the absolute number of desired tokens, but this requires knowing the difficulty of the problem beforehand to appropriately set the token budget for a query. To address these issues, we propose Adaptive Effort Control, a self-adaptive reinforcement learning method that trains models to use a user-specified fraction of tokens relative to the current average chain-of-thought length for each query. This approach eliminates dataset- and phase-specific tuning while producing better cost-accuracy tradeoff curves compared to standard methods. Users can dynamically adjust the cost-accuracy trade-off through a continuous effort parameter specified at inference time. We observe that the model automatically learns to allocate resources proportionally to the task difficulty and, across model scales ranging from 1.5B to 32B parameters, our approach enables approximately 3x reduction in chain-of-thought length while maintaining or improving performance relative to the base model used for RL training.
Maximally-Informative Retrieval for State Space Model Generation
Jun 13, 2025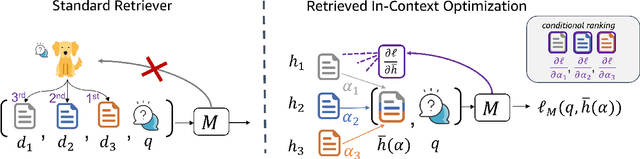
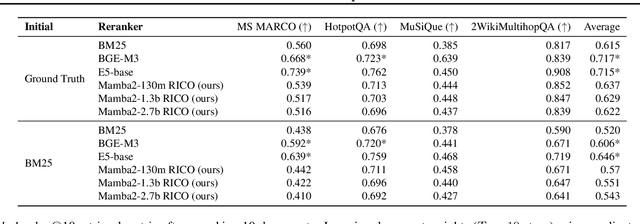
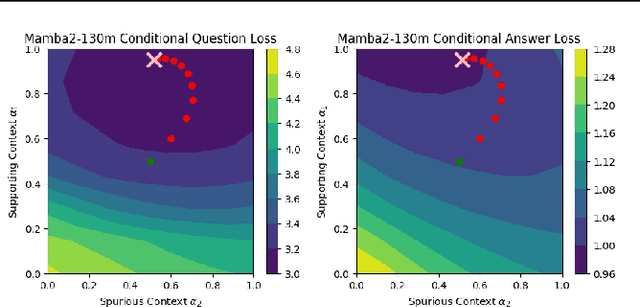
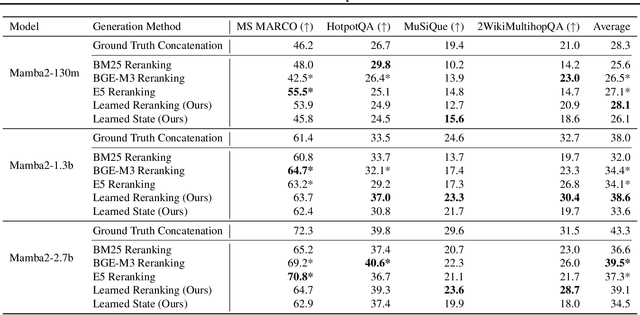
Abstract:Given a query and dataset, the optimal way of answering the query is to make use all the information available. Modern LLMs exhibit impressive ability to memorize training data, but data not deemed important during training is forgotten, and information outside that training set cannot be made use of. Processing an entire dataset at inference time is infeasible due to the bounded nature of model resources (e.g. context size in transformers or states in state space models), meaning we must resort to external memory. This constraint naturally leads to the following problem: How can we decide based on the present query and model, what among a virtually unbounded set of known data matters for inference? To minimize model uncertainty for a particular query at test-time, we introduce Retrieval In-Context Optimization (RICO), a retrieval method that uses gradients from the LLM itself to learn the optimal mixture of documents for answer generation. Unlike traditional retrieval-augmented generation (RAG), which relies on external heuristics for document retrieval, our approach leverages direct feedback from the model. Theoretically, we show that standard top-$k$ retrieval with model gradients can approximate our optimization procedure, and provide connections to the leave-one-out loss. We demonstrate empirically that by minimizing an unsupervised loss objective in the form of question perplexity, we can achieve comparable retriever metric performance to BM25 with \emph{no finetuning}. Furthermore, when evaluated on quality of the final prediction, our method often outperforms fine-tuned dense retrievers such as E5.
PICASO: Permutation-Invariant Context Composition with State Space Models
Feb 24, 2025



Abstract:Providing Large Language Models with relevant contextual knowledge at inference time has been shown to greatly improve the quality of their generations. This is often achieved by prepending informative passages of text, or 'contexts', retrieved from external knowledge bases to their input. However, processing additional contexts online incurs significant computation costs that scale with their length. State Space Models (SSMs) offer a promising solution by allowing a database of contexts to be mapped onto fixed-dimensional states from which to start the generation. A key challenge arises when attempting to leverage information present across multiple contexts, since there is no straightforward way to condition generation on multiple independent states in existing SSMs. To address this, we leverage a simple mathematical relation derived from SSM dynamics to compose multiple states into one that efficiently approximates the effect of concatenating textual contexts. Since the temporal ordering of contexts can often be uninformative, we enforce permutation-invariance by efficiently averaging states obtained via our composition algorithm across all possible context orderings. We evaluate our resulting method on WikiText and MSMARCO in both zero-shot and fine-tuned settings, and show that we can match the strongest performing baseline while enjoying on average 5.4x speedup.
Descriminative-Generative Custom Tokens for Vision-Language Models
Feb 17, 2025



Abstract:This paper explores the possibility of learning custom tokens for representing new concepts in Vision-Language Models (VLMs). Our aim is to learn tokens that can be effective for both discriminative and generative tasks while composing well with words to form new input queries. The targeted concept is specified in terms of a small set of images and a parent concept described using text. We operate on CLIP text features and propose to use a combination of a textual inversion loss and a classification loss to ensure that text features of the learned token are aligned with image features of the concept in the CLIP embedding space. We restrict the learned token to a low-dimensional subspace spanned by tokens for attributes that are appropriate for the given super-class. These modifications improve the quality of compositions of the learned token with natural language for generating new scenes. Further, we show that learned custom tokens can be used to form queries for text-to-image retrieval task, and also have the important benefit that composite queries can be visualized to ensure that the desired concept is faithfully encoded. Based on this, we introduce the method of Generation Aided Image Retrieval, where the query is modified at inference time to better suit the search intent. On the DeepFashion2 dataset, our method improves Mean Reciprocal Retrieval (MRR) over relevant baselines by 7%.
An Invitation to Neuroalgebraic Geometry
Jan 31, 2025



Abstract:In this expository work, we promote the study of function spaces parameterized by machine learning models through the lens of algebraic geometry. To this end, we focus on algebraic models, such as neural networks with polynomial activations, whose associated function spaces are semi-algebraic varieties. We outline a dictionary between algebro-geometric invariants of these varieties, such as dimension, degree, and singularities, and fundamental aspects of machine learning, such as sample complexity, expressivity, training dynamics, and implicit bias. Along the way, we review the literature and discuss ideas beyond the algebraic domain. This work lays the foundations of a research direction bridging algebraic geometry and deep learning, that we refer to as neuroalgebraic geometry.
Geometry and Optimization of Shallow Polynomial Networks
Jan 10, 2025

Abstract:We study shallow neural networks with polynomial activations. The function space for these models can be identified with a set of symmetric tensors with bounded rank. We describe general features of these networks, focusing on the relationship between width and optimization. We then consider teacher-student problems, that can be viewed as a problem of low-rank tensor approximation with respect to a non-standard inner product that is induced by the data distribution. In this setting, we introduce a teacher-metric discriminant which encodes the qualitative behavior of the optimization as a function of the training data distribution. Finally, we focus on networks with quadratic activations, presenting an in-depth analysis of the optimization landscape. In particular, we present a variation of the Eckart-Young Theorem characterizing all critical points and their Hessian signatures for teacher-student problems with quadratic networks and Gaussian training data.
The N-Grammys: Accelerating Autoregressive Inference with Learning-Free Batched Speculation
Nov 06, 2024



Abstract:Speculative decoding aims to speed up autoregressive generation of a language model by verifying in parallel the tokens generated by a smaller draft model.In this work, we explore the effectiveness of learning-free, negligible-cost draft strategies, namely $N$-grams obtained from the model weights and the context. While the predicted next token of the base model is rarely the top prediction of these simple strategies, we observe that it is often within their top-$k$ predictions for small $k$. Based on this, we show that combinations of simple strategies can achieve significant inference speedups over different tasks. The overall performance is comparable to more complex methods, yet does not require expensive preprocessing or modification of the base model, and allows for seamless `plug-and-play' integration into pipelines.
Compositional Structures in Neural Embedding and Interaction Decompositions
Jul 12, 2024


Abstract:We describe a basic correspondence between linear algebraic structures within vector embeddings in artificial neural networks and conditional independence constraints on the probability distributions modeled by these networks. Our framework aims to shed light on the emergence of structural patterns in data representations, a phenomenon widely acknowledged but arguably still lacking a solid formal grounding. Specifically, we introduce a characterization of compositional structures in terms of "interaction decompositions," and we establish necessary and sufficient conditions for the presence of such structures within the representations of a model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge