The N-Grammys: Accelerating Autoregressive Inference with Learning-Free Batched Speculation

Speculative decoding aims to speed up autoregressive generation of a language model by verifying in parallel the tokens generated by a smaller draft model.In this work, we explore the effectiveness of learning-free, negligible-cost draft strategies, namely $N$-grams obtained from the model weights and the context. While the predicted next token of the base model is rarely the top prediction of these simple strategies, we observe that it is often within their top-$k$ predictions for small $k$. Based on this, we show that combinations of simple strategies can achieve significant inference speedups over different tasks. The overall performance is comparable to more complex methods, yet does not require expensive preprocessing or modification of the base model, and allows for seamless `plug-and-play' integration into pipelines.

BASS: Batched Attention-optimized Speculative Sampling

Speculative decoding has emerged as a powerful method to improve latency and throughput in hosting large language models. However, most existing implementations focus on generating a single sequence. Real-world generative AI applications often require multiple responses and how to perform speculative decoding in a batched setting while preserving its latency benefits poses non-trivial challenges. This paper describes a system of batched speculative decoding that sets a new state of the art in multi-sequence generation latency and that demonstrates superior GPU utilization as well as quality of generations within a time budget. For example, for a 7.8B-size model on a single A100 GPU and with a batch size of 8, each sequence is generated at an average speed of 5.8ms per token, the overall throughput being 1.1K tokens per second. These results represent state-of-the-art latency and a 2.15X speed-up over optimized regular decoding. Within a time budget that regular decoding does not finish, our system is able to generate sequences with HumanEval Pass@First of 43% and Pass@All of 61%, far exceeding what's feasible with single-sequence speculative decoding. Our peak GPU utilization during decoding reaches as high as 15.8%, more than 3X the highest of that of regular decoding and around 10X of single-sequence speculative decoding.

Token Alignment via Character Matching for Subword Completion

Generative models, widely utilized in various applications, can often struggle with prompts corresponding to partial tokens. This struggle stems from tokenization, where partial tokens fall out of distribution during inference, leading to incorrect or nonsensical outputs. This paper examines a technique to alleviate the tokenization artifact on text completion in generative models, maintaining performance even in regular non-subword cases. The method, termed token alignment, involves backtracking to the last complete tokens and ensuring the model's generation aligns with the prompt. This approach showcases marked improvement across many partial token scenarios, including nuanced cases like space-prefix and partial indentation, with only a minor time increase. The technique and analysis detailed in this paper contribute to the continuous advancement of generative models in handling partial inputs, bearing relevance for applications like code completion and text autocompletion.

Bifurcated Attention for Single-Context Large-Batch Sampling

In our study, we present bifurcated attention, a method developed for language model inference in single-context batch sampling contexts. This approach aims to reduce redundant memory IO costs, a significant factor in latency for high batch sizes and long context lengths. Bifurcated attention achieves this by dividing the attention mechanism during incremental decoding into two distinct GEMM operations, focusing on the KV cache from prefill and the decoding process. This method ensures precise computation and maintains the usual computational load (FLOPs) of standard attention mechanisms, but with reduced memory IO. Bifurcated attention is also compatible with multi-query attention mechanism known for reduced memory IO for KV cache, further enabling higher batch size and context length. The resulting efficiency leads to lower latency, improving suitability for real-time applications, e.g., enabling massively-parallel answer generation without substantially increasing latency, enhancing performance when integrated with postprocessing techniques such as reranking.

Multi-lingual Evaluation of Code Generation Models

We present MBXP, an execution-based code completion benchmark in 10+ programming languages. This collection of datasets is generated by our conversion framework that translates prompts and test cases from the original MBPP dataset to the corresponding data in a target language. Based on this benchmark, we are able to evaluate code generation models in a multi-lingual fashion, and in particular discover generalization ability of language models on out-of-domain languages, advantages of large multi-lingual models over mono-lingual, benefits of few-shot prompting, and zero-shot translation abilities. In addition, we use our code generation model to perform large-scale bootstrapping to obtain synthetic canonical solutions in several languages. These solutions can be used for other code-related evaluations such as insertion-based, summarization, or code translation tasks where we demonstrate results and release as part of our benchmark.

Fundamental Limits on Energy-Delay-Accuracy of In-memory Architectures in Inference Applications

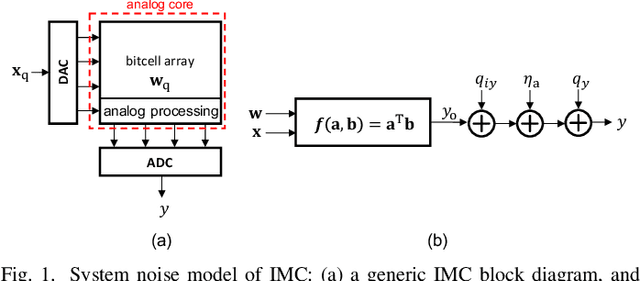
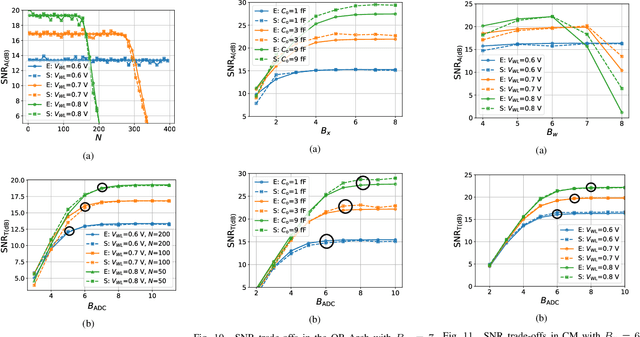
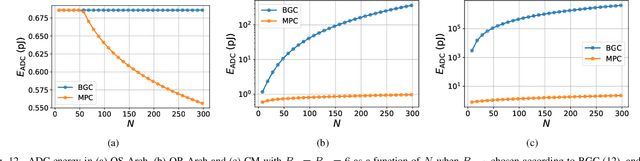
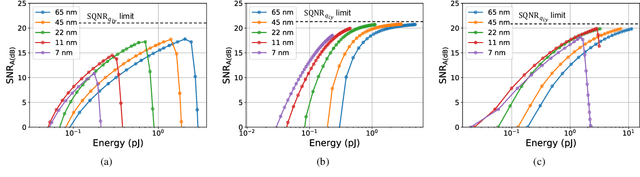
This paper obtains fundamental limits on the computational precision of in-memory computing architectures (IMCs). An IMC noise model and associated SNR metrics are defined and their interrelationships analyzed to show that the accuracy of IMCs is fundamentally limited by the compute SNR ($\text{SNR}_{\text{a}}$) of its analog core, and that activation, weight and output precision needs to be assigned appropriately for the final output SNR $\text{SNR}_{\text{T}} \rightarrow \text{SNR}_{\text{a}}$. The minimum precision criterion (MPC) is proposed to minimize the ADC precision. Three in-memory compute models - charge summing (QS), current summing (IS) and charge redistribution (QR) - are shown to underlie most known IMCs. Noise, energy and delay expressions for the compute models are developed and employed to derive expressions for the SNR, ADC precision, energy, and latency of IMCs. The compute SNR expressions are validated via Monte Carlo simulations in a 65 nm CMOS process. For a 512 row SRAM array, it is shown that: 1) IMCs have an upper bound on their maximum achievable $\text{SNR}_{\text{a}}$ due to constraints on energy, area and voltage swing, and this upper bound reduces with technology scaling for QS-based architectures; 2) MPC enables $\text{SNR}_{\text{T}} \rightarrow \text{SNR}_{\text{a}}$ to be realized with minimal ADC precision; 3) QS-based (QR-based) architectures are preferred for low (high) compute SNR scenarios.