Efficient motion planning for problems lacking optimal substructure

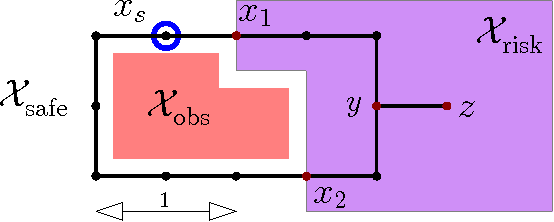
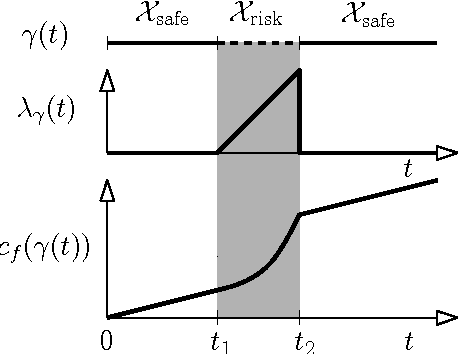
We consider the motion-planning problem of planning a collision-free path of a robot in the presence of risk zones. The robot is allowed to travel in these zones but is penalized in a super-linear fashion for consecutive accumulative time spent there. We suggest a natural cost function that balances path length and risk-exposure time. Specifically, we consider the discrete setting where we are given a graph, or a roadmap, and we wish to compute the minimal-cost path under this cost function. Interestingly, paths defined using our cost function do not have an optimal substructure. Namely, subpaths of an optimal path are not necessarily optimal. Thus, the Bellman condition is not satisfied and standard graph-search algorithms such as Dijkstra cannot be used. We present a path-finding algorithm, which can be seen as a natural generalization of Dijkstra's algorithm. Our algorithm runs in $O\left((n_B\cdot n) \log( n_B\cdot n) + n_B\cdot m\right)$ time, where~$n$ and $m$ are the number of vertices and edges of the graph, respectively, and $n_B$ is the number of intersections between edges and the boundary of the risk zone. We present simulations on robotic platforms demonstrating both the natural paths produced by our cost function and the computational efficiency of our algorithm.

Hybrid control trajectory optimization under uncertainty

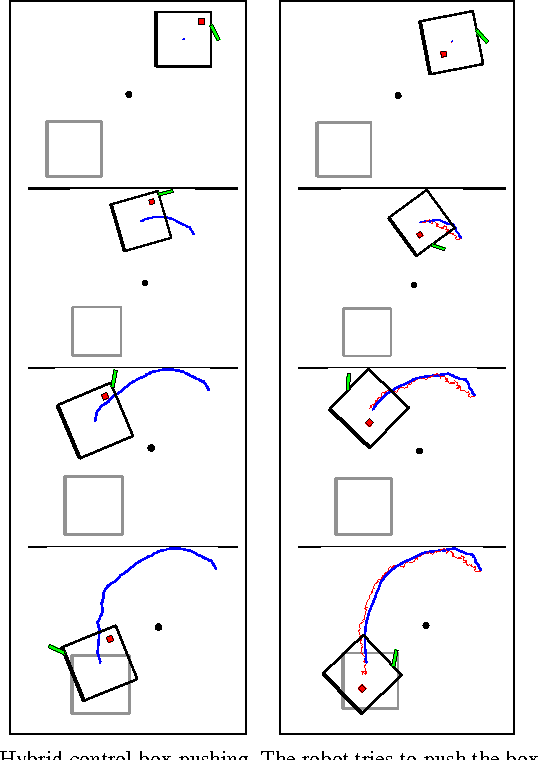
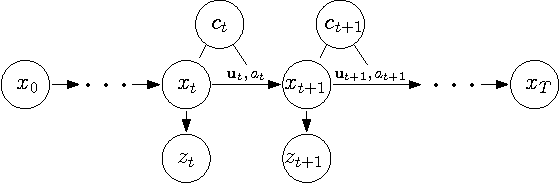
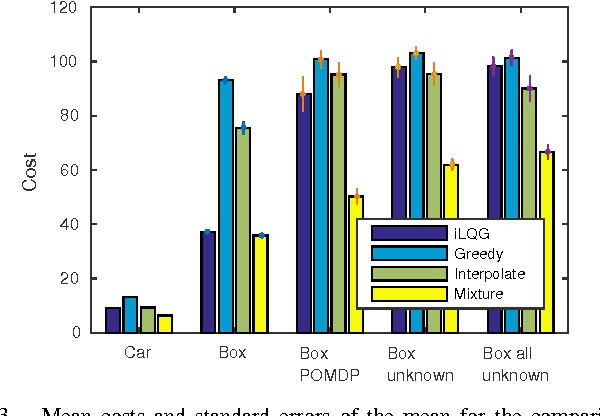
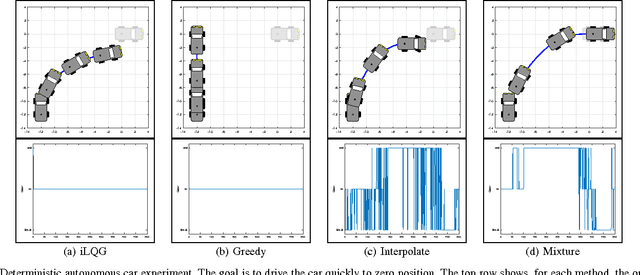
Trajectory optimization is a fundamental problem in robotics. While optimization of continuous control trajectories is well developed, many applications require both discrete and continuous, i.e., hybrid, controls. Finding an optimal sequence of hybrid controls is challenging due to the exponential explosion of discrete control combinations. Our method, based on Differential Dynamic Programming (DDP), circumvents this problem by incorporating discrete actions inside DDP: we first optimize continuous mixtures of discrete actions, and, subsequently force the mixtures into fully discrete actions. Moreover, we show how our approach can be extended to partially observable Markov decision processes (POMDPs) for trajectory planning under uncertainty. We validate the approach in a car driving problem where the robot has to switch discrete gears and in a box pushing application where the robot can switch the side of the box to push. The pose and the friction parameters of the pushed box are initially unknown and only indirectly observable.

Human-Robot Mutual Adaptation in Shared Autonomy

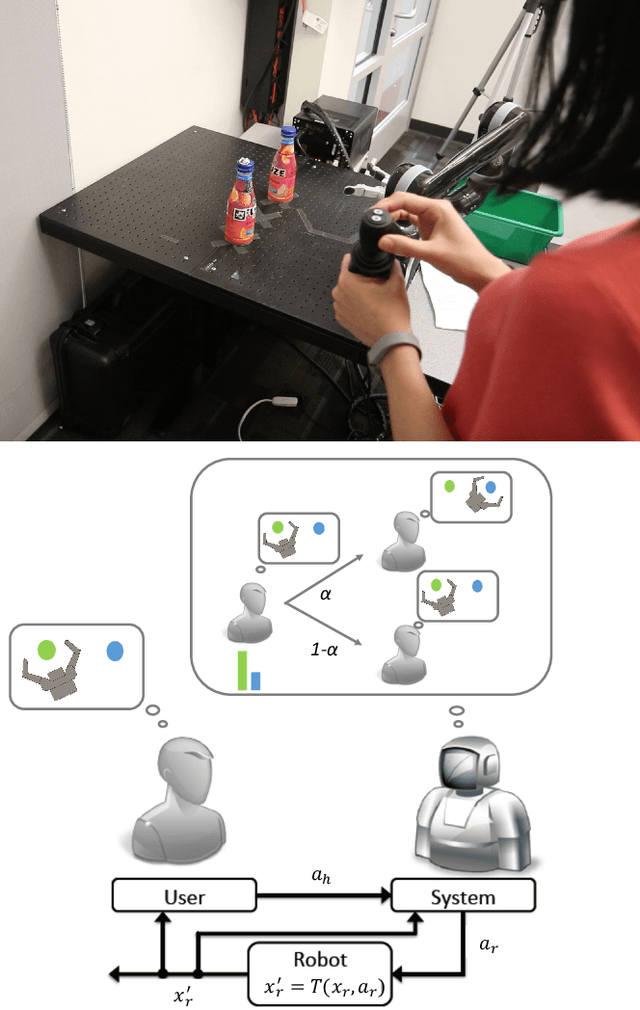
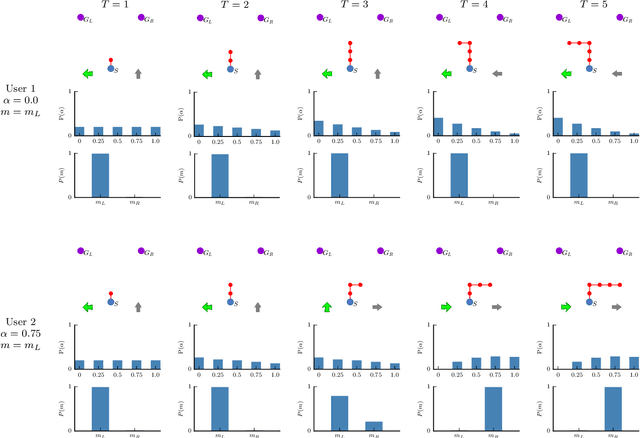
Shared autonomy integrates user input with robot autonomy in order to control a robot and help the user to complete a task. Our work aims to improve the performance of such a human-robot team: the robot tries to guide the human towards an effective strategy, sometimes against the human's own preference, while still retaining his trust. We achieve this through a principled human-robot mutual adaptation formalism. We integrate a bounded-memory adaptation model of the human into a partially observable stochastic decision model, which enables the robot to adapt to an adaptable human. When the human is adaptable, the robot guides the human towards a good strategy, maybe unknown to the human in advance. When the human is stubborn and not adaptable, the robot complies with the human's preference in order to retain their trust. In the shared autonomy setting, unlike many other common human-robot collaboration settings, only the robot actions can change the physical state of the world, and the human and robot goals are not fully observable. We address these challenges and show in a human subject experiment that the proposed mutual adaptation formalism improves human-robot team performance, while retaining a high level of user trust in the robot, compared to the common approach of having the robot strictly following participants' preference.

Functional Gradient Motion Planning in Reproducing Kernel Hilbert Spaces

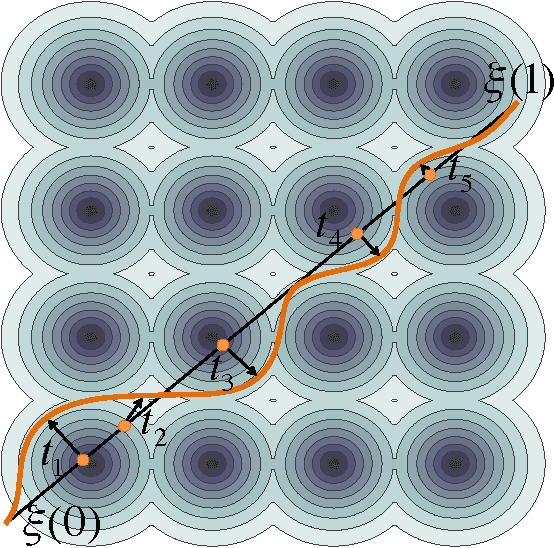
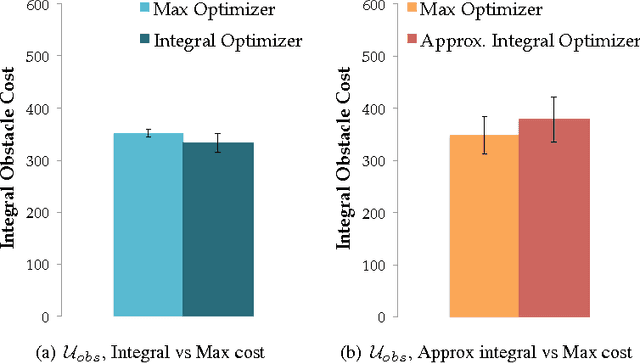
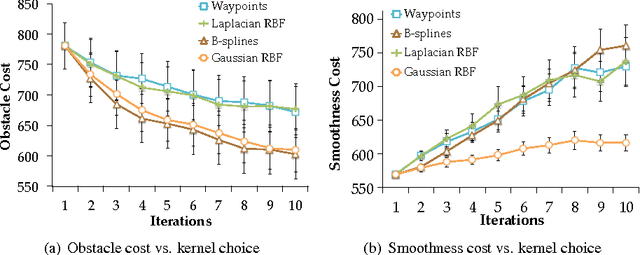
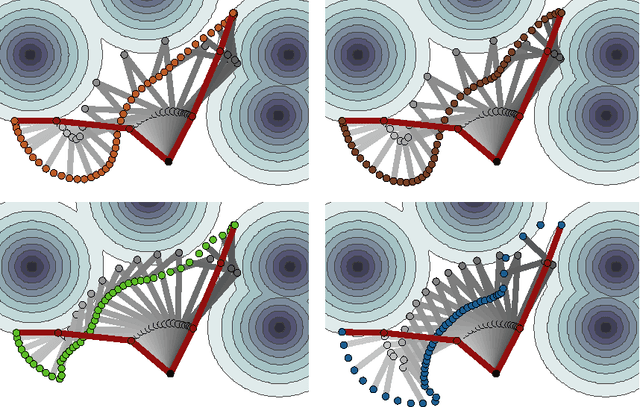
We introduce a functional gradient descent trajectory optimization algorithm for robot motion planning in Reproducing Kernel Hilbert Spaces (RKHSs). Functional gradient algorithms are a popular choice for motion planning in complex many-degree-of-freedom robots, since they (in theory) work by directly optimizing within a space of continuous trajectories to avoid obstacles while maintaining geometric properties such as smoothness. However, in practice, functional gradient algorithms typically commit to a fixed, finite parameterization of trajectories, often as a list of waypoints. Such a parameterization can lose much of the benefit of reasoning in a continuous trajectory space: e.g., it can require taking an inconveniently small step size and large number of iterations to maintain smoothness. Our work generalizes functional gradient trajectory optimization by formulating it as minimization of a cost functional in an RKHS. This generalization lets us represent trajectories as linear combinations of kernel functions, without any need for waypoints. As a result, we are able to take larger steps and achieve a locally optimal trajectory in just a few iterations. Depending on the selection of kernel, we can directly optimize in spaces of trajectories that are inherently smooth in velocity, jerk, curvature, etc., and that have a low-dimensional, adaptively chosen parameterization. Our experiments illustrate the effectiveness of the planner for different kernels, including Gaussian RBFs, Laplacian RBFs, and B-splines, as compared to the standard discretized waypoint representation.

Benchmarking in Manipulation Research: The YCB Object and Model Set and Benchmarking Protocols

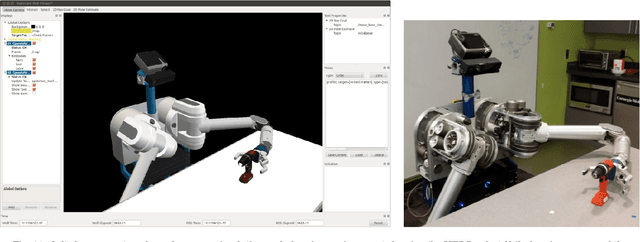
In this paper we present the Yale-CMU-Berkeley (YCB) Object and Model set, intended to be used to facilitate benchmarking in robotic manipulation, prosthetic design and rehabilitation research. The objects in the set are designed to cover a wide range of aspects of the manipulation problem; it includes objects of daily life with different shapes, sizes, textures, weight and rigidity, as well as some widely used manipulation tests. The associated database provides high-resolution RGBD scans, physical properties, and geometric models of the objects for easy incorporation into manipulation and planning software platforms. In addition to describing the objects and models in the set along with how they were chosen and derived, we provide a framework and a number of example task protocols, laying out how the set can be used to quantitatively evaluate a range of manipulation approaches including planning, learning, mechanical design, control, and many others. A comprehensive literature survey on existing benchmarks and object datasets is also presented and their scope and limitations are discussed. The set will be freely distributed to research groups worldwide at a series of tutorials at robotics conferences, and will be otherwise available at a reasonable purchase cost. It is our hope that the ready availability of this set along with the ground laid in terms of protocol templates will enable the community of manipulation researchers to more easily compare approaches as well as continually evolve benchmarking tests as the field matures.

Near Optimal Bayesian Active Learning for Decision Making

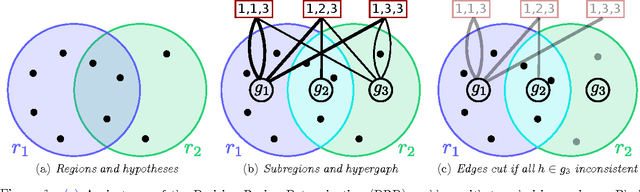
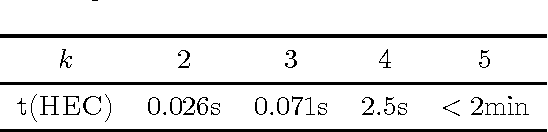
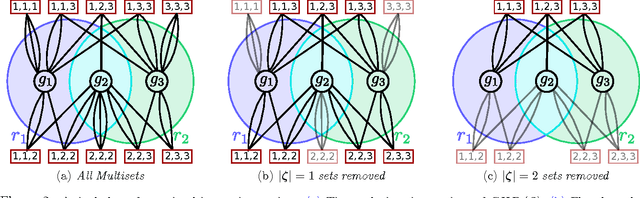
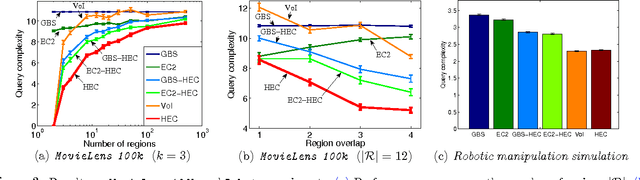
How should we gather information to make effective decisions? We address Bayesian active learning and experimental design problems, where we sequentially select tests to reduce uncertainty about a set of hypotheses. Instead of minimizing uncertainty per se, we consider a set of overlapping decision regions of these hypotheses. Our goal is to drive uncertainty into a single decision region as quickly as possible. We identify necessary and sufficient conditions for correctly identifying a decision region that contains all hypotheses consistent with observations. We develop a novel Hyperedge Cutting (HEC) algorithm for this problem, and prove that is competitive with the intractable optimal policy. Our efficient implementation of the algorithm relies on computing subsets of the complete homogeneous symmetric polynomials. Finally, we demonstrate its effectiveness on two practical applications: approximate comparison-based learning and active localization using a robot manipulator.