InstaHide: Instance-hiding Schemes for Private Distributed Learning

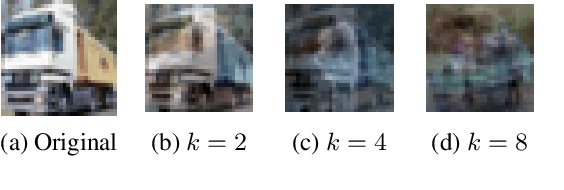
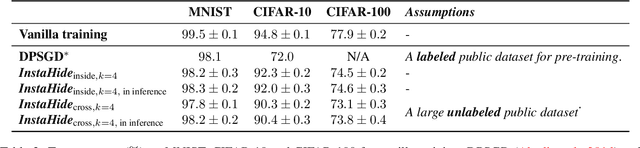
How can multiple distributed entities collaboratively train a shared deep net on their private data while preserving privacy? This paper introduces InstaHide, a simple encryption of training images, which can be plugged into existing distributed deep learning pipelines. The encryption is efficient and applying it during training has minor effect on test accuracy. InstaHide encrypts each training image with a "one-time secret key" which consists of mixing a number of randomly chosen images and applying a random pixel-wise mask. Other contributions of this paper include: (a) Using a large public dataset (e.g. ImageNet) for mixing during its encryption, which improves security. (b) Experimental results to show effectiveness in preserving privacy against known attacks with only minor effects on accuracy. (c) Theoretical analysis showing that successfully attacking privacy requires attackers to solve a difficult computational problem. (d) Demonstrating that use of the pixel-wise mask is important for security, since Mixup alone is shown to be insecure to some some efficient attacks. (e) Release of a challenge dataset https://github.com/Hazelsuko07/InstaHide_Challenge Our code is available at https://github.com/Hazelsuko07/InstaHide

Privacy-preserving Learning via Deep Net Pruning

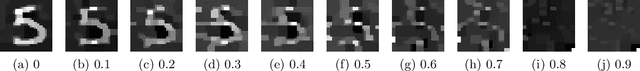
This paper attempts to answer the question whether neural network pruning can be used as a tool to achieve differential privacy without losing much data utility. As a first step towards understanding the relationship between neural network pruning and differential privacy, this paper proves that pruning a given layer of the neural network is equivalent to adding a certain amount of differentially private noise to its hidden-layer activations. The paper also presents experimental results to show the practical implications of the theoretical finding and the key parameter values in a simple practical setting. These results show that neural network pruning can be a more effective alternative to adding differentially private noise for neural networks.

A Sample Complexity Separation between Non-Convex and Convex Meta-Learning

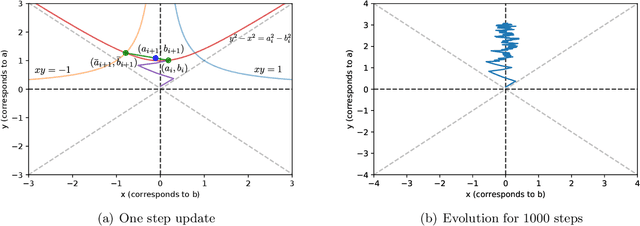
One popular trend in meta-learning is to learn from many training tasks a common initialization for a gradient-based method that can be used to solve a new task with few samples. The theory of meta-learning is still in its early stages, with several recent learning-theoretic analyses of methods such as Reptile [Nichol et al., 2018] being for convex models. This work shows that convex-case analysis might be insufficient to understand the success of meta-learning, and that even for non-convex models it is important to look inside the optimization black-box, specifically at properties of the optimization trajectory. We construct a simple meta-learning instance that captures the problem of one-dimensional subspace learning. For the convex formulation of linear regression on this instance, we show that the new task sample complexity of any initialization-based meta-learning algorithm is $\Omega(d)$, where $d$ is the input dimension. In contrast, for the non-convex formulation of a two layer linear network on the same instance, we show that both Reptile and multi-task representation learning can have new task sample complexity of $\mathcal{O}(1)$, demonstrating a separation from convex meta-learning. Crucially, analyses of the training dynamics of these methods reveal that they can meta-learn the correct subspace onto which the data should be projected.

Provable Representation Learning for Imitation Learning via Bi-level Optimization

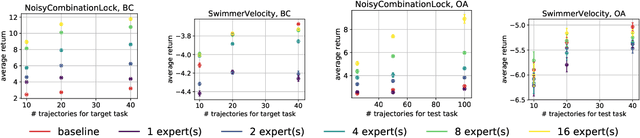
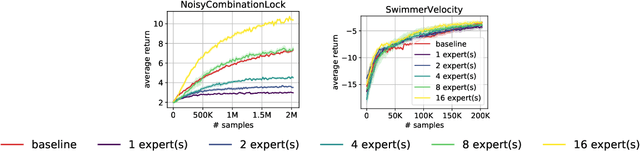
A common strategy in modern learning systems is to learn a representation that is useful for many tasks, a.k.a. representation learning. We study this strategy in the imitation learning setting for Markov decision processes (MDPs) where multiple experts' trajectories are available. We formulate representation learning as a bi-level optimization problem where the "outer" optimization tries to learn the joint representation and the "inner" optimization encodes the imitation learning setup and tries to learn task-specific parameters. We instantiate this framework for the imitation learning settings of behavior cloning and observation-alone. Theoretically, we show using our framework that representation learning can provide sample complexity benefits for imitation learning in both settings. We also provide proof-of-concept experiments to verify our theory.

Over-parameterized Adversarial Training: An Analysis Overcoming the Curse of Dimensionality

Adversarial training is a popular method to give neural nets robustness against adversarial perturbations. In practice adversarial training leads to low robust training loss. However, a rigorous explanation for why this happens under natural conditions is still missing. Recently a convergence theory for standard (non-adversarial) supervised training was developed by various groups for {\em very overparametrized} nets. It is unclear how to extend these results to adversarial training because of the min-max objective. Recently, a first step towards this direction was made by Gao et al. using tools from online learning, but they require the width of the net to be \emph{exponential} in input dimension $d$, and with an unnatural activation function. Our work proves convergence to low robust training loss for \emph{polynomial} width instead of exponential, under natural assumptions and with the ReLU activation. Key element of our proof is showing that ReLU networks near initialization can approximate the step function, which may be of independent interest.

An Exponential Learning Rate Schedule for Deep Learning

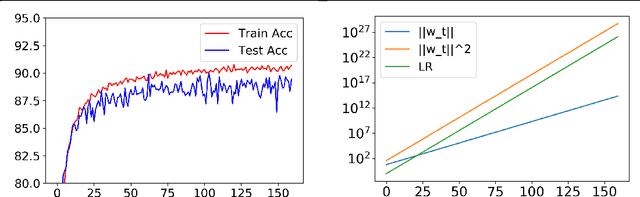
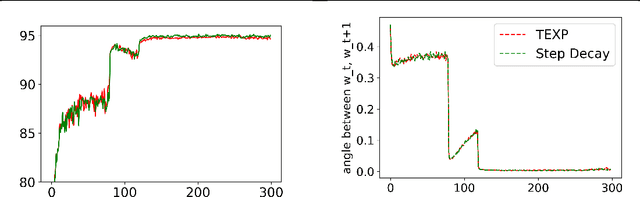
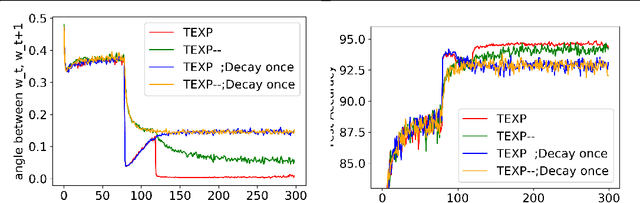
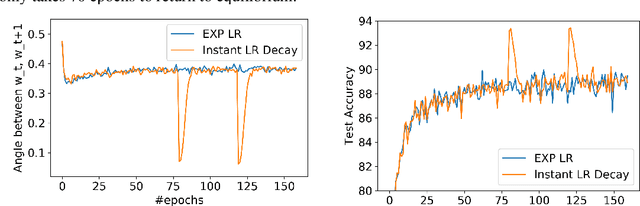
Intriguing empirical evidence exists that deep learning can work well with exoticschedules for varying the learning rate. This paper suggests that the phenomenon may be due to Batch Normalization or BN, which is ubiquitous and provides benefits in optimization and generalization across all standard architectures. The following new results are shown about BN with weight decay and momentum (in other words, the typical use case which was not considered in earlier theoretical analyses of stand-alone BN. 1. Training can be done using SGD with momentum and an exponentially increasing learning rate schedule, i.e., learning rate increases by some $(1 +\alpha)$ factor in every epoch for some $\alpha >0$. (Precise statement in the paper.) To the best of our knowledge this is the first time such a rate schedule has been successfully used, let alone for highly successful architectures. As expected, such training rapidly blows up network weights, but the net stays well-behaved due to normalization. 2. Mathematical explanation of the success of the above rate schedule: a rigorous proof that it is equivalent to the standard setting of BN + SGD + StandardRate Tuning + Weight Decay + Momentum. This equivalence holds for other normalization layers as well, Group Normalization, LayerNormalization, Instance Norm, etc. 3. A worked-out toy example illustrating the above linkage of hyper-parameters. Using either weight decay or BN alone reaches global minimum, but convergence fails when both are used.

Enhanced Convolutional Neural Tangent Kernels

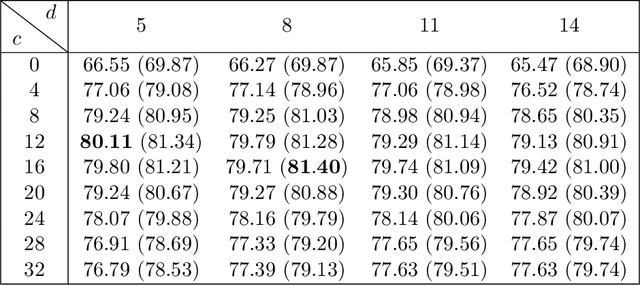
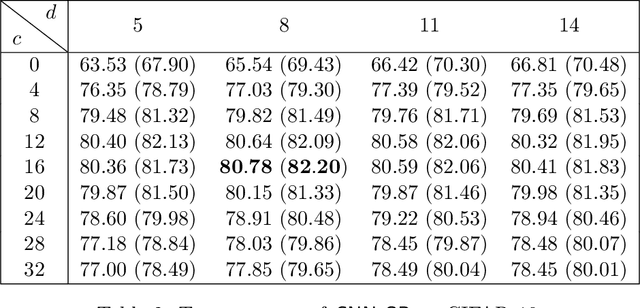
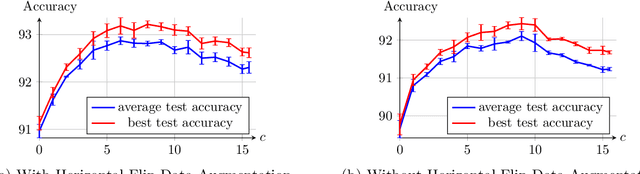
Recent research shows that for training with $\ell_2$ loss, convolutional neural networks (CNNs) whose width (number of channels in convolutional layers) goes to infinity correspond to regression with respect to the CNN Gaussian Process kernel (CNN-GP) if only the last layer is trained, and correspond to regression with respect to the Convolutional Neural Tangent Kernel (CNTK) if all layers are trained. An exact algorithm to compute CNTK (Arora et al., 2019) yielded the finding that classification accuracy of CNTK on CIFAR-10 is within 6-7% of that of that of the corresponding CNN architecture (best figure being around 78%) which is interesting performance for a fixed kernel. Here we show how to significantly enhance the performance of these kernels using two ideas. (1) Modifying the kernel using a new operation called Local Average Pooling (LAP) which preserves efficient computability of the kernel and inherits the spirit of standard data augmentation using pixel shifts. Earlier papers were unable to incorporate naive data augmentation because of the quadratic training cost of kernel regression. This idea is inspired by Global Average Pooling (GAP), which we show for CNN-GP and CNTK is equivalent to full translation data augmentation. (2) Representing the input image using a pre-processing technique proposed by Coates et al. (2011), which uses a single convolutional layer composed of random image patches. On CIFAR-10, the resulting kernel, CNN-GP with LAP and horizontal flip data augmentation, achieves 89% accuracy, matching the performance of AlexNet (Krizhevsky et al., 2012). Note that this is the best such result we know of for a classifier that is not a trained neural network. Similar improvements are obtained for Fashion-MNIST.

Harnessing the Power of Infinitely Wide Deep Nets on Small-data Tasks

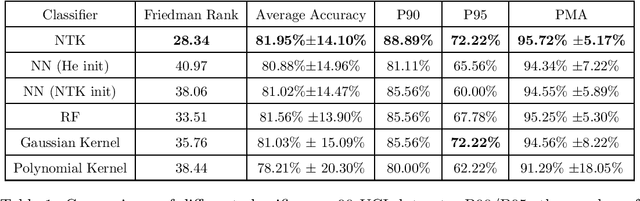
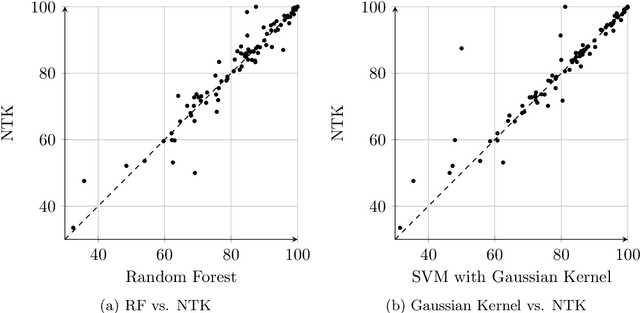
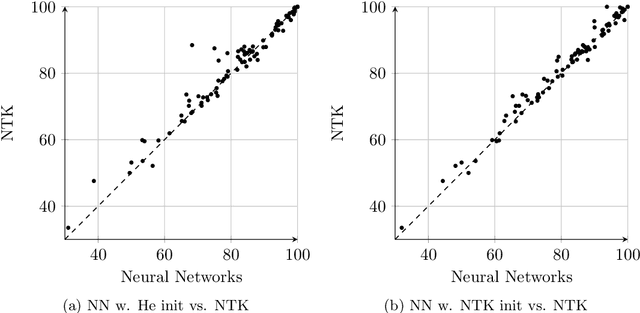
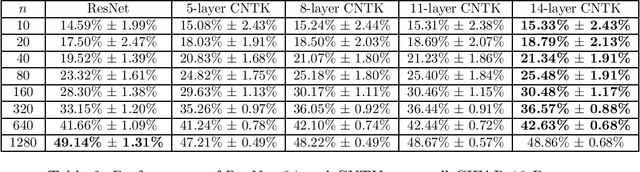
Recent research shows that the following two models are equivalent: (a) infinitely wide neural networks (NNs) trained under l2 loss by gradient descent with infinitesimally small learning rate (b) kernel regression with respect to so-called Neural Tangent Kernels (NTKs) (Jacot et al., 2018). An efficient algorithm to compute the NTK, as well as its convolutional counterparts, appears in Arora et al. (2019a), which allowed studying performance of infinitely wide nets on datasets like CIFAR-10. However, super-quadratic running time of kernel methods makes them best suited for small-data tasks. We report results suggesting neural tangent kernels perform strongly on low-data tasks. 1. On a standard testbed of classification/regression tasks from the UCI database, NTK SVM beats the previous gold standard, Random Forests (RF), and also the corresponding finite nets. 2. On CIFAR-10 with 10 - 640 training samples, Convolutional NTK consistently beats ResNet-34 by 1% - 3%. 3. On VOC07 testbed for few-shot image classification tasks on ImageNet with transfer learning (Goyal et al., 2019), replacing the linear SVM currently used with a Convolutional NTK SVM consistently improves performance. 4. Comparing the performance of NTK with the finite-width net it was derived from, NTK behavior starts at lower net widths than suggested by theoretical analysis(Arora et al., 2019a). NTK's efficacy may trace to lower variance of output.

Explaining Landscape Connectivity of Low-cost Solutions for Multilayer Nets

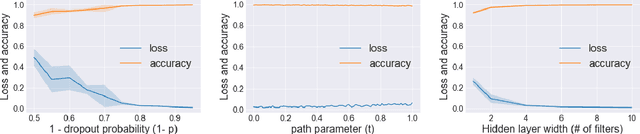
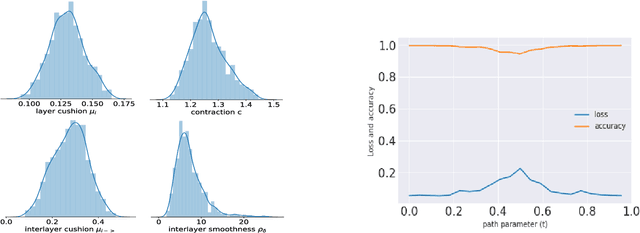
Mode connectivity is a surprising phenomenon in the loss landscape of deep nets. Optima---at least those discovered by gradient-based optimization---turn out to be connected by simple paths on which the loss function is almost constant. Often, these paths can be chosen to be piece-wise linear, with as few as two segments. We give mathematical explanations for this phenomenon, assuming generic properties (such as dropout stability and noise stability) of well-trained deep nets, which have previously been identified as part of understanding the generalization properties of deep nets. Our explanation holds for realistic multilayer nets, and experiments are presented to verify the theory.

A Simple Saliency Method That Passes the Sanity Checks

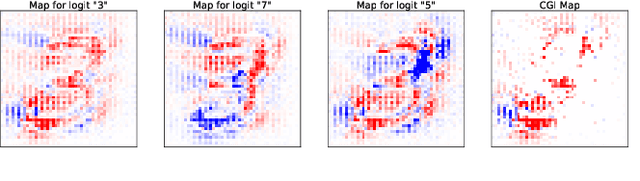
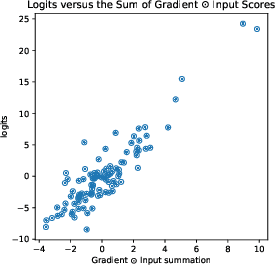
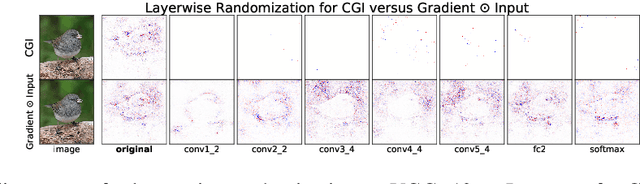
There is great interest in "saliency methods" (also called "attribution methods"), which give "explanations" for a deep net's decision, by assigning a "score" to each feature/pixel in the input. Their design usually involves credit-assignment via the gradient of the output with respect to input. Recently Adebayo et al. [arXiv:1810.03292] questioned the validity of many of these methods since they do not pass simple *sanity checks* which test whether the scores shift/vanish when layers of the trained net are randomized, or when the net is retrained using random labels for inputs. We propose a simple fix to existing saliency methods that helps them pass sanity checks, which we call "competition for pixels". This involves computing saliency maps for all possible labels in the classification task, and using a simple competition among them to identify and remove less relevant pixels from the map. The simplest variant of this is "Competitive Gradient $\odot$ Input (CGI)": it is efficient, requires no additional training, and uses only the input and gradient. Some theoretical justification is provided for it (especially for ReLU networks) and its performance is empirically demonstrated.