Provable learning of Noisy-or Networks

Many machine learning applications use latent variable models to explain structure in data, whereby visible variables (= coordinates of the given datapoint) are explained as a probabilistic function of some hidden variables. Finding parameters with the maximum likelihood is NP-hard even in very simple settings. In recent years, provably efficient algorithms were nevertheless developed for models with linear structures: topic models, mixture models, hidden markov models, etc. These algorithms use matrix or tensor decomposition, and make some reasonable assumptions about the parameters of the underlying model. But matrix or tensor decomposition seems of little use when the latent variable model has nonlinearities. The current paper shows how to make progress: tensor decomposition is applied for learning the single-layer {\em noisy or} network, which is a textbook example of a Bayes net, and used for example in the classic QMR-DT software for diagnosing which disease(s) a patient may have by observing the symptoms he/she exhibits. The technical novelty here, which should be useful in other settings in future, is analysis of tensor decomposition in presence of systematic error (i.e., where the noise/error is correlated with the signal, and doesn't decrease as number of samples goes to infinity). This requires rethinking all steps of tensor decomposition methods from the ground up. For simplicity our analysis is stated assuming that the network parameters were chosen from a probability distribution but the method seems more generally applicable.

Efficient Algorithms for Large-scale Generalized Eigenvector Computation and Canonical Correlation Analysis

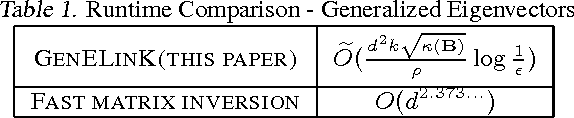
This paper considers the problem of canonical-correlation analysis (CCA) (Hotelling, 1936) and, more broadly, the generalized eigenvector problem for a pair of symmetric matrices. These are two fundamental problems in data analysis and scientific computing with numerous applications in machine learning and statistics (Shi and Malik, 2000; Hardoon et al., 2004; Witten et al., 2009). We provide simple iterative algorithms, with improved runtimes, for solving these problems that are globally linearly convergent with moderate dependencies on the condition numbers and eigenvalue gaps of the matrices involved. We obtain our results by reducing CCA to the top-$k$ generalized eigenvector problem. We solve this problem through a general framework that simply requires black box access to an approximate linear system solver. Instantiating this framework with accelerated gradient descent we obtain a running time of $O(\frac{z k \sqrt{\kappa}}{\rho} \log(1/\epsilon) \log \left(k\kappa/\rho\right))$ where $z$ is the total number of nonzero entries, $\kappa$ is the condition number and $\rho$ is the relative eigenvalue gap of the appropriate matrices. Our algorithm is linear in the input size and the number of components $k$ up to a $\log(k)$ factor. This is essential for handling large-scale matrices that appear in practice. To the best of our knowledge this is the first such algorithm with global linear convergence. We hope that our results prompt further research and ultimately improve the practical running time for performing these important data analysis procedures on large data sets.

Provable Algorithms for Inference in Topic Models

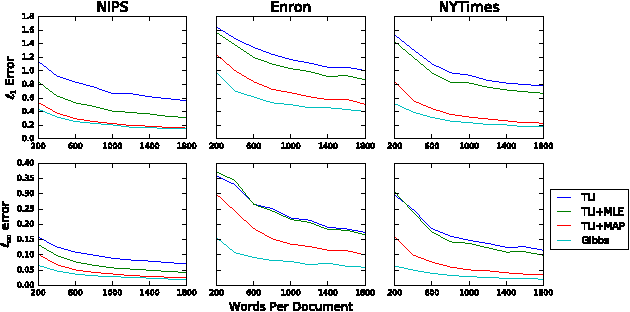
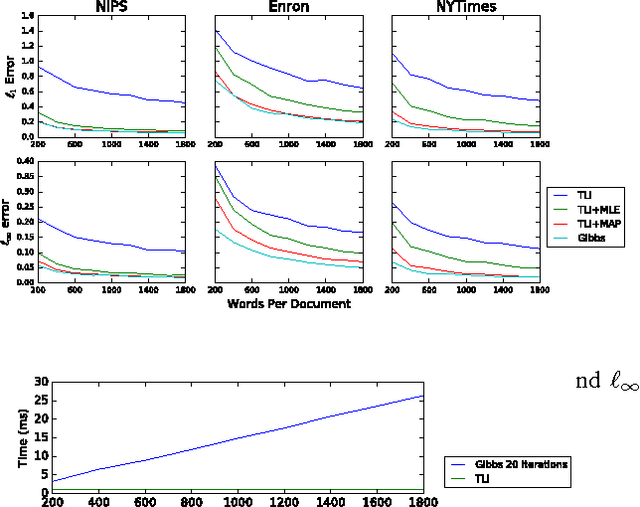
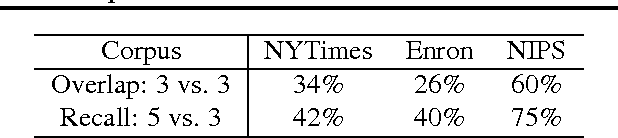
Recently, there has been considerable progress on designing algorithms with provable guarantees -- typically using linear algebraic methods -- for parameter learning in latent variable models. But designing provable algorithms for inference has proven to be more challenging. Here we take a first step towards provable inference in topic models. We leverage a property of topic models that enables us to construct simple linear estimators for the unknown topic proportions that have small variance, and consequently can work with short documents. Our estimators also correspond to finding an estimate around which the posterior is well-concentrated. We show lower bounds that for shorter documents it can be information theoretically impossible to find the hidden topics. Finally, we give empirical results that demonstrate that our algorithm works on realistic topic models. It yields good solutions on synthetic data and runs in time comparable to a {\em single} iteration of Gibbs sampling.

Efficient approaches for escaping higher order saddle points in non-convex optimization

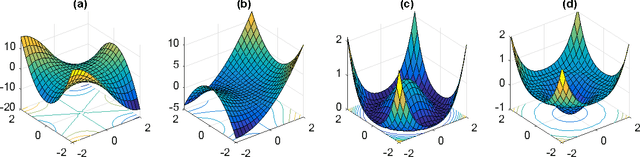
Local search heuristics for non-convex optimizations are popular in applied machine learning. However, in general it is hard to guarantee that such algorithms even converge to a local minimum, due to the existence of complicated saddle point structures in high dimensions. Many functions have degenerate saddle points such that the first and second order derivatives cannot distinguish them with local optima. In this paper we use higher order derivatives to escape these saddle points: we design the first efficient algorithm guaranteed to converge to a third order local optimum (while existing techniques are at most second order). We also show that it is NP-hard to extend this further to finding fourth order local optima.

Minimal Realization Problems for Hidden Markov Models

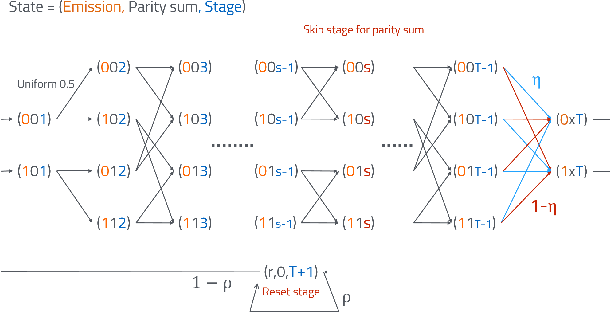
Consider a stationary discrete random process with alphabet size d, which is assumed to be the output process of an unknown stationary Hidden Markov Model (HMM). Given the joint probabilities of finite length strings of the process, we are interested in finding a finite state generative model to describe the entire process. In particular, we focus on two classes of models: HMMs and quasi-HMMs, which is a strictly larger class of models containing HMMs. In the main theorem, we show that if the random process is generated by an HMM of order less or equal than k, and whose transition and observation probability matrix are in general position, namely almost everywhere on the parameter space, both the minimal quasi-HMM realization and the minimal HMM realization can be efficiently computed based on the joint probabilities of all the length N strings, for N > 4 lceil log_d(k) rceil +1. In this paper, we also aim to compare and connect the two lines of literature: realization theory of HMMs, and the recent development in learning latent variable models with tensor decomposition techniques.

Analyzing Tensor Power Method Dynamics in Overcomplete Regime

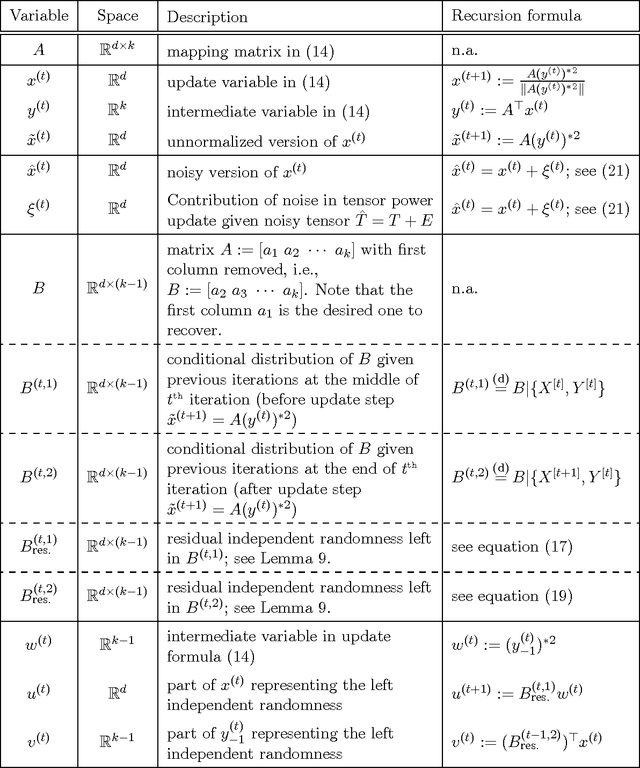
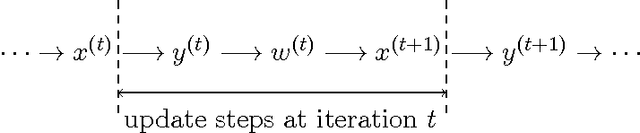
We present a novel analysis of the dynamics of tensor power iterations in the overcomplete regime where the tensor CP rank is larger than the input dimension. Finding the CP decomposition of an overcomplete tensor is NP-hard in general. We consider the case where the tensor components are randomly drawn, and show that the simple power iteration recovers the components with bounded error under mild initialization conditions. We apply our analysis to unsupervised learning of latent variable models, such as multi-view mixture models and spherical Gaussian mixtures. Given the third order moment tensor, we learn the parameters using tensor power iterations. We prove it can correctly learn the model parameters when the number of hidden components $k$ is much larger than the data dimension $d$, up to $k = o(d^{1.5})$. We initialize the power iterations with data samples and prove its success under mild conditions on the signal-to-noise ratio of the samples. Our analysis significantly expands the class of latent variable models where spectral methods are applicable. Our analysis also deals with noise in the input tensor leading to sample complexity result in the application to learning latent variable models.

Rich Component Analysis

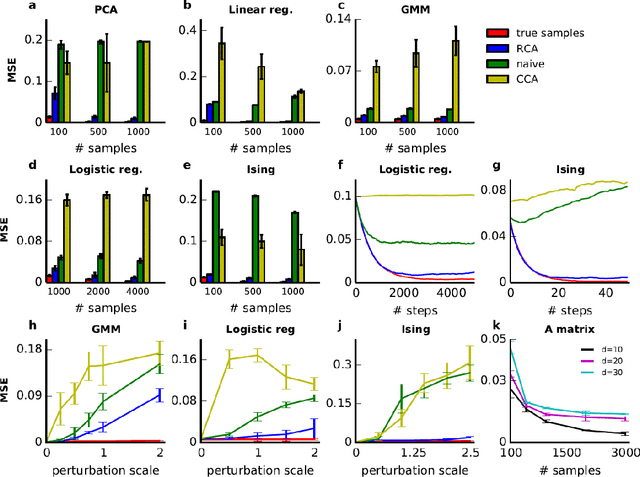
In many settings, we have multiple data sets (also called views) that capture different and overlapping aspects of the same phenomenon. We are often interested in finding patterns that are unique to one or to a subset of the views. For example, we might have one set of molecular observations and one set of physiological observations on the same group of individuals, and we want to quantify molecular patterns that are uncorrelated with physiology. Despite being a common problem, this is highly challenging when the correlations come from complex distributions. In this paper, we develop the general framework of Rich Component Analysis (RCA) to model settings where the observations from different views are driven by different sets of latent components, and each component can be a complex, high-dimensional distribution. We introduce algorithms based on cumulant extraction that provably learn each of the components without having to model the other components. We show how to integrate RCA with stochastic gradient descent into a meta-algorithm for learning general models, and demonstrate substantial improvement in accuracy on several synthetic and real datasets in both supervised and unsupervised tasks. Our method makes it possible to learn latent variable models when we don't have samples from the true model but only samples after complex perturbations.

Intersecting Faces: Non-negative Matrix Factorization With New Guarantees

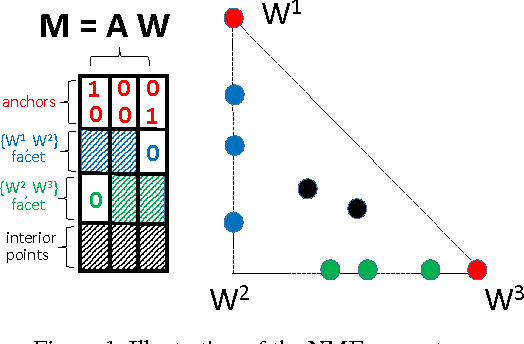
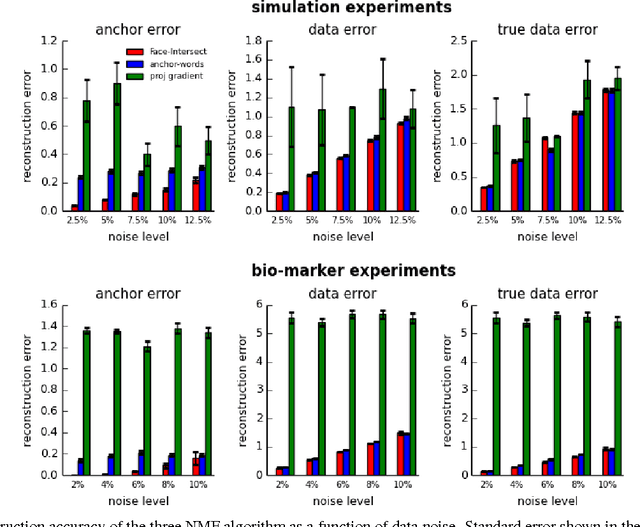
Non-negative matrix factorization (NMF) is a natural model of admixture and is widely used in science and engineering. A plethora of algorithms have been developed to tackle NMF, but due to the non-convex nature of the problem, there is little guarantee on how well these methods work. Recently a surge of research have focused on a very restricted class of NMFs, called separable NMF, where provably correct algorithms have been developed. In this paper, we propose the notion of subset-separable NMF, which substantially generalizes the property of separability. We show that subset-separability is a natural necessary condition for the factorization to be unique or to have minimum volume. We developed the Face-Intersect algorithm which provably and efficiently solves subset-separable NMF under natural conditions, and we prove that our algorithm is robust to small noise. We explored the performance of Face-Intersect on simulations and discuss settings where it empirically outperformed the state-of-art methods. Our work is a step towards finding provably correct algorithms that solve large classes of NMF problems.

Un-regularizing: approximate proximal point and faster stochastic algorithms for empirical risk minimization

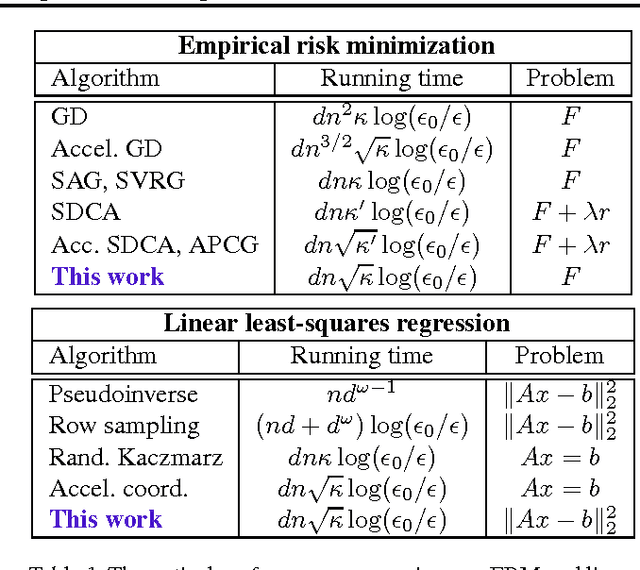
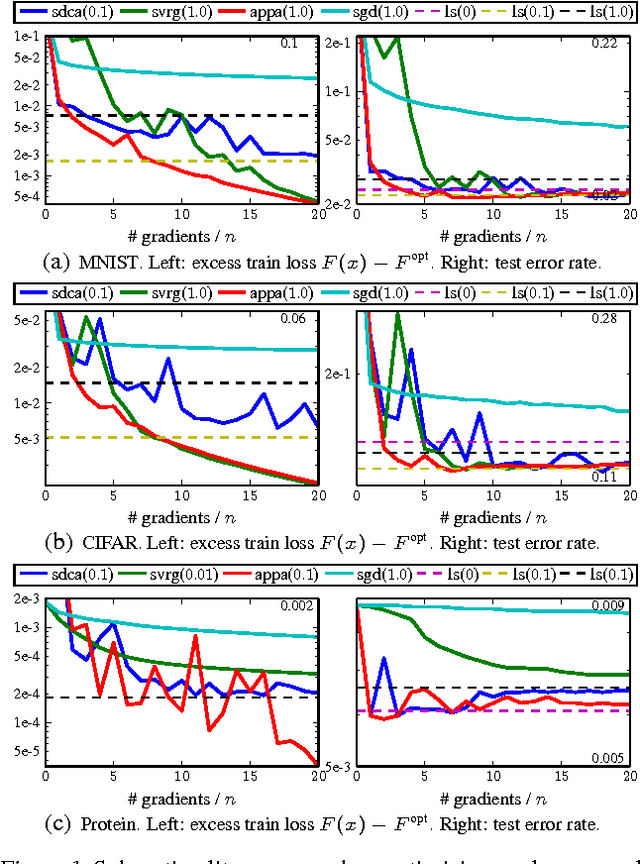
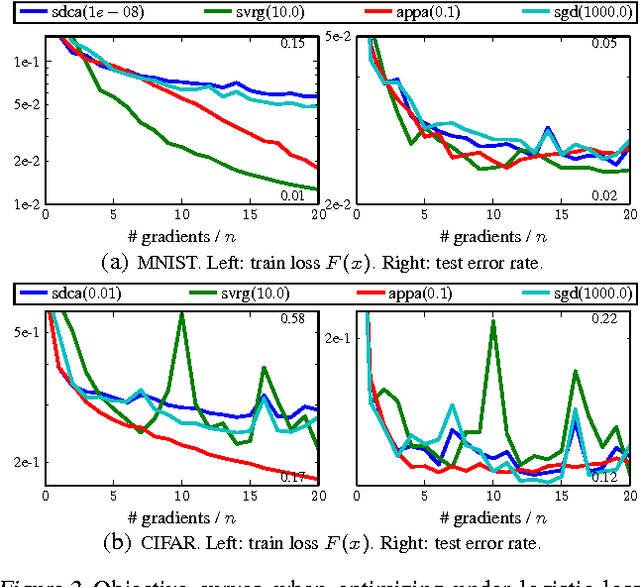
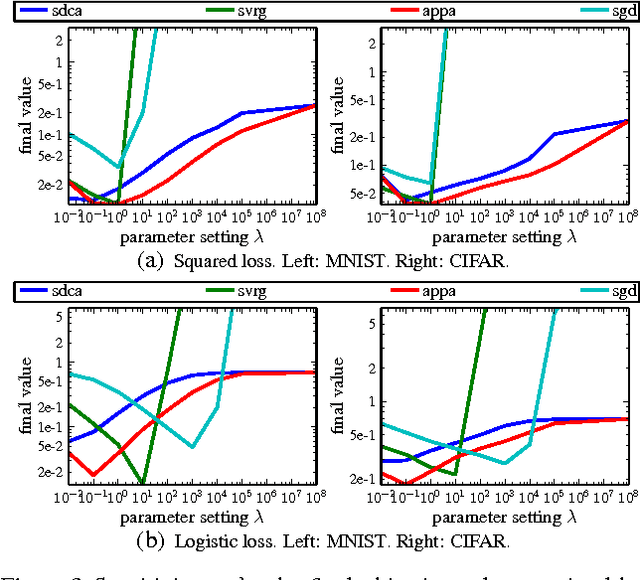
We develop a family of accelerated stochastic algorithms that minimize sums of convex functions. Our algorithms improve upon the fastest running time for empirical risk minimization (ERM), and in particular linear least-squares regression, across a wide range of problem settings. To achieve this, we establish a framework based on the classical proximal point algorithm. Namely, we provide several algorithms that reduce the minimization of a strongly convex function to approximate minimizations of regularizations of the function. Using these results, we accelerate recent fast stochastic algorithms in a black-box fashion. Empirically, we demonstrate that the resulting algorithms exhibit notions of stability that are advantageous in practice. Both in theory and in practice, the provided algorithms reap the computational benefits of adding a large strongly convex regularization term, without incurring a corresponding bias to the original problem.

Decomposing Overcomplete 3rd Order Tensors using Sum-of-Squares Algorithms

Tensor rank and low-rank tensor decompositions have many applications in learning and complexity theory. Most known algorithms use unfoldings of tensors and can only handle rank up to $n^{\lfloor p/2 \rfloor}$ for a $p$-th order tensor in $\mathbb{R}^{n^p}$. Previously no efficient algorithm can decompose 3rd order tensors when the rank is super-linear in the dimension. Using ideas from sum-of-squares hierarchy, we give the first quasi-polynomial time algorithm that can decompose a random 3rd order tensor decomposition when the rank is as large as $n^{3/2}/\textrm{polylog} n$. We also give a polynomial time algorithm for certifying the injective norm of random low rank tensors. Our tensor decomposition algorithm exploits the relationship between injective norm and the tensor components. The proof relies on interesting tools for decoupling random variables to prove better matrix concentration bounds, which can be useful in other settings.