Parallel Sampling via Autospeculation

We present parallel algorithms to accelerate sampling via counting in two settings: any-order autoregressive models and denoising diffusion models. An any-order autoregressive model accesses a target distribution $μ$ on $[q]^n$ through an oracle that provides conditional marginals, while a denoising diffusion model accesses a target distribution $μ$ on $\mathbb{R}^n$ through an oracle that provides conditional means under Gaussian noise. Standard sequential sampling algorithms require $\widetilde{O}(n)$ time to produce a sample from $μ$ in either setting. We show that, by issuing oracle calls in parallel, the expected sampling time can be reduced to $\widetilde{O}(n^{1/2})$. This improves the previous $\widetilde{O}(n^{2/3})$ bound for any-order autoregressive models and yields the first parallel speedup for diffusion models in the high-accuracy regime, under the relatively mild assumption that the support of $μ$ is bounded. We introduce a novel technique to obtain our results: speculative rejection sampling. This technique leverages an auxiliary ``speculative'' distribution~$ν$ that approximates~$μ$ to accelerate sampling. Our technique is inspired by the well-studied ``speculative decoding'' techniques popular in large language models, but differs in key ways. Firstly, we use ``autospeculation,'' namely we build the speculation $ν$ out of the same oracle that defines~$μ$. In contrast, speculative decoding typically requires a separate, faster, but potentially less accurate ``draft'' model $ν$. Secondly, the key differentiating factor in our technique is that we make and accept speculations at a ``sequence'' level rather than at the level of single (or a few) steps. This last fact is key to unlocking our parallel runtime of $\widetilde{O}(n^{1/2})$.

Stein's unbiased risk estimate and Hyvärinen's score matching

We study two G-modeling strategies for estimating the signal distribution (the empirical Bayesian's prior) from observations corrupted with normal noise. First, we choose the signal distribution by minimizing Stein's unbiased risk estimate (SURE) of the implied Eddington/Tweedie Bayes denoiser, an approach motivated by optimal empirical Bayesian shrinkage estimation of the signals. Second, we select the signal distribution by minimizing Hyv\"arinen's score matching objective for the implied score (derivative of log-marginal density), targeting minimal Fisher divergence between estimated and true marginal densities. While these strategies appear distinct, they are known to be mathematically equivalent. We provide a unified analysis of SURE and score matching under both well-specified signal distribution classes and misspecification. In the classical well-specified setting with homoscedastic noise and compactly supported signal distribution, we establish nearly parametric rates of convergence of the empirical Bayes regret and the Fisher divergence. In a commonly studied misspecified model, we establish fast rates of convergence to the oracle denoiser and corresponding oracle inequalities. Our empirical results demonstrate competitiveness with nonparametric maximum likelihood in well-specified settings, while showing superior performance under misspecification, particularly in settings involving heteroscedasticity and side information.

Efficiently learning and sampling multimodal distributions with data-based initialization

We consider the problem of sampling a multimodal distribution with a Markov chain given a small number of samples from the stationary measure. Although mixing can be arbitrarily slow, we show that if the Markov chain has a $k$th order spectral gap, initialization from a set of $\tilde O(k/\varepsilon^2)$ samples from the stationary distribution will, with high probability over the samples, efficiently generate a sample whose conditional law is $\varepsilon$-close in TV distance to the stationary measure. In particular, this applies to mixtures of $k$ distributions satisfying a Poincar\'e inequality, with faster convergence when they satisfy a log-Sobolev inequality. Our bounds are stable to perturbations to the Markov chain, and in particular work for Langevin diffusion over $\mathbb R^d$ with score estimation error, as well as Glauber dynamics combined with approximation error from pseudolikelihood estimation. This justifies the success of data-based initialization for score matching methods despite slow mixing for the data distribution, and improves and generalizes the results of Koehler and Vuong (2023) to have linear, rather than exponential, dependence on $k$ and apply to arbitrary semigroups. As a consequence of our results, we show for the first time that a natural class of low-complexity Ising measures can be efficiently learned from samples.

Inferring Dynamic Networks from Marginals with Iterative Proportional Fitting

A common network inference problem, arising from real-world data constraints, is how to infer a dynamic network from its time-aggregated adjacency matrix and time-varying marginals (i.e., row and column sums). Prior approaches to this problem have repurposed the classic iterative proportional fitting (IPF) procedure, also known as Sinkhorn's algorithm, with promising empirical results. However, the statistical foundation for using IPF has not been well understood: under what settings does IPF provide principled estimation of a dynamic network from its marginals, and how well does it estimate the network? In this work, we establish such a setting, by identifying a generative network model whose maximum likelihood estimates are recovered by IPF. Our model both reveals implicit assumptions on the use of IPF in such settings and enables new analyses, such as structure-dependent error bounds on IPF's parameter estimates. When IPF fails to converge on sparse network data, we introduce a principled algorithm that guarantees IPF converges under minimal changes to the network structure. Finally, we conduct experiments with synthetic and real-world data, which demonstrate the practical value of our theoretical and algorithmic contributions.

Lasso with Latents: Efficient Estimation, Covariate Rescaling, and Computational-Statistical Gaps

It is well-known that the statistical performance of Lasso can suffer significantly when the covariates of interest have strong correlations. In particular, the prediction error of Lasso becomes much worse than computationally inefficient alternatives like Best Subset Selection. Due to a large conjectured computational-statistical tradeoff in the problem of sparse linear regression, it may be impossible to close this gap in general. In this work, we propose a natural sparse linear regression setting where strong correlations between covariates arise from unobserved latent variables. In this setting, we analyze the problem caused by strong correlations and design a surprisingly simple fix. While Lasso with standard normalization of covariates fails, there exists a heterogeneous scaling of the covariates with which Lasso will suddenly obtain strong provable guarantees for estimation. Moreover, we design a simple, efficient procedure for computing such a "smart scaling." The sample complexity of the resulting "rescaled Lasso" algorithm incurs (in the worst case) quadratic dependence on the sparsity of the underlying signal. While this dependence is not information-theoretically necessary, we give evidence that it is optimal among the class of polynomial-time algorithms, via the method of low-degree polynomials. This argument reveals a new connection between sparse linear regression and a special version of sparse PCA with a near-critical negative spike. The latter problem can be thought of as a real-valued analogue of learning a sparse parity. Using it, we also establish the first computational-statistical gap for the closely related problem of learning a Gaussian Graphical Model.

Sampling Multimodal Distributions with the Vanilla Score: Benefits of Data-Based Initialization

There is a long history, as well as a recent explosion of interest, in statistical and generative modeling approaches based on score functions -- derivatives of the log-likelihood of a distribution. In seminal works, Hyv\"arinen proposed vanilla score matching as a way to learn distributions from data by computing an estimate of the score function of the underlying ground truth, and established connections between this method and established techniques like Contrastive Divergence and Pseudolikelihood estimation. It is by now well-known that vanilla score matching has significant difficulties learning multimodal distributions. Although there are various ways to overcome this difficulty, the following question has remained unanswered -- is there a natural way to sample multimodal distributions using just the vanilla score? Inspired by a long line of related experimental works, we prove that the Langevin diffusion with early stopping, initialized at the empirical distribution, and run on a score function estimated from data successfully generates natural multimodal distributions (mixtures of log-concave distributions).

Uniform Convergence with Square-Root Lipschitz Loss

We establish generic uniform convergence guarantees for Gaussian data in terms of the Rademacher complexity of the hypothesis class and the Lipschitz constant of the square root of the scalar loss function. We show how these guarantees substantially generalize previous results based on smoothness (Lipschitz constant of the derivative), and allow us to handle the broader class of square-root-Lipschitz losses, which includes also non-smooth loss functions appropriate for studying phase retrieval and ReLU regression, as well as rederive and better understand "optimistic rate" and interpolation learning guarantees.

Feature Adaptation for Sparse Linear Regression

Sparse linear regression is a central problem in high-dimensional statistics. We study the correlated random design setting, where the covariates are drawn from a multivariate Gaussian $N(0,\Sigma)$, and we seek an estimator with small excess risk. If the true signal is $t$-sparse, information-theoretically, it is possible to achieve strong recovery guarantees with only $O(t\log n)$ samples. However, computationally efficient algorithms have sample complexity linear in (some variant of) the condition number of $\Sigma$. Classical algorithms such as the Lasso can require significantly more samples than necessary even if there is only a single sparse approximate dependency among the covariates. We provide a polynomial-time algorithm that, given $\Sigma$, automatically adapts the Lasso to tolerate a small number of approximate dependencies. In particular, we achieve near-optimal sample complexity for constant sparsity and if $\Sigma$ has few ``outlier'' eigenvalues. Our algorithm fits into a broader framework of feature adaptation for sparse linear regression with ill-conditioned covariates. With this framework, we additionally provide the first polynomial-factor improvement over brute-force search for constant sparsity $t$ and arbitrary covariance $\Sigma$.

Statistical Efficiency of Score Matching: The View from Isoperimetry

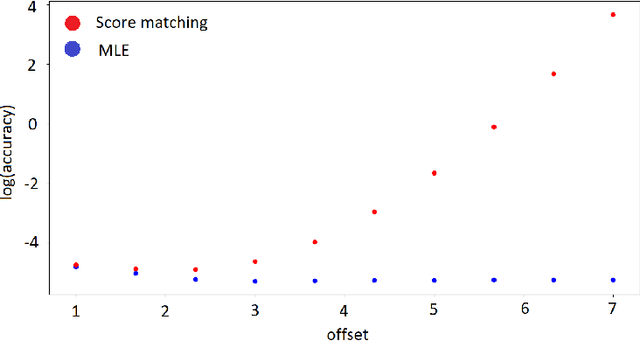
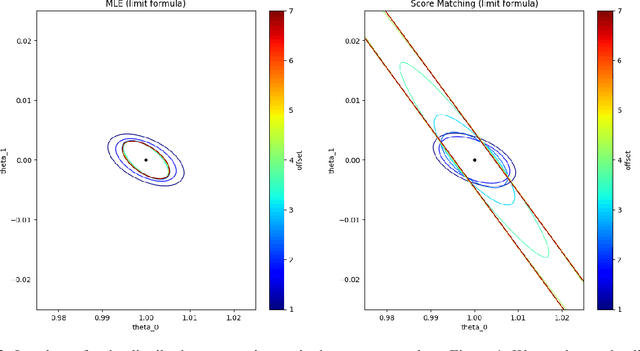
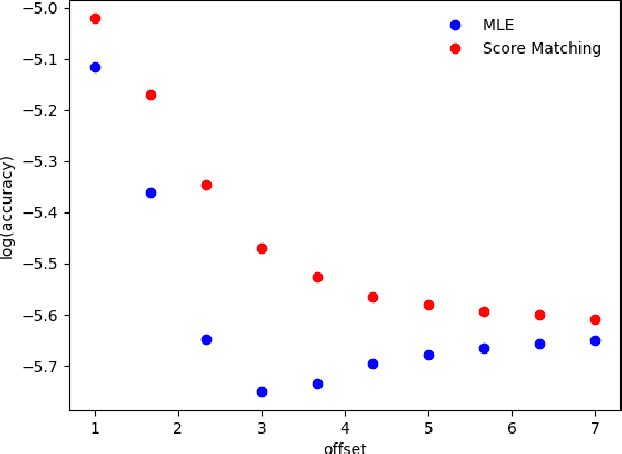
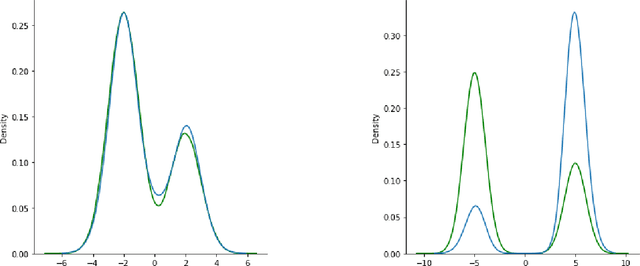
Deep generative models parametrized up to a normalizing constant (e.g. energy-based models) are difficult to train by maximizing the likelihood of the data because the likelihood and/or gradients thereof cannot be explicitly or efficiently written down. Score matching is a training method, whereby instead of fitting the likelihood $\log p(x)$ for the training data, we instead fit the score function $\nabla_x \log p(x)$ -- obviating the need to evaluate the partition function. Though this estimator is known to be consistent, its unclear whether (and when) its statistical efficiency is comparable to that of maximum likelihood -- which is known to be (asymptotically) optimal. We initiate this line of inquiry in this paper, and show a tight connection between statistical efficiency of score matching and the isoperimetric properties of the distribution being estimated -- i.e. the Poincar\'e, log-Sobolev and isoperimetric constant -- quantities which govern the mixing time of Markov processes like Langevin dynamics. Roughly, we show that the score matching estimator is statistically comparable to the maximum likelihood when the distribution has a small isoperimetric constant. Conversely, if the distribution has a large isoperimetric constant -- even for simple families of distributions like exponential families with rich enough sufficient statistics -- score matching will be substantially less efficient than maximum likelihood. We suitably formalize these results both in the finite sample regime, and in the asymptotic regime. Finally, we identify a direct parallel in the discrete setting, where we connect the statistical properties of pseudolikelihood estimation with approximate tensorization of entropy and the Glauber dynamics.

Distributional Hardness Against Preconditioned Lasso via Erasure-Robust Designs

Sparse linear regression with ill-conditioned Gaussian random designs is widely believed to exhibit a statistical/computational gap, but there is surprisingly little formal evidence for this belief, even in the form of examples that are hard for restricted classes of algorithms. Recent work has shown that, for certain covariance matrices, the broad class of Preconditioned Lasso programs provably cannot succeed on polylogarithmically sparse signals with a sublinear number of samples. However, this lower bound only shows that for every preconditioner, there exists at least one signal that it fails to recover successfully. This leaves open the possibility that, for example, trying multiple different preconditioners solves every sparse linear regression problem. In this work, we prove a stronger lower bound that overcomes this issue. For an appropriate covariance matrix, we construct a single signal distribution on which any invertibly-preconditioned Lasso program fails with high probability, unless it receives a linear number of samples. Surprisingly, at the heart of our lower bound is a new positive result in compressed sensing. We show that standard sparse random designs are with high probability robust to adversarial measurement erasures, in the sense that if $b$ measurements are erased, then all but $O(b)$ of the coordinates of the signal are still information-theoretically identifiable. To our knowledge, this is the first time that partial recoverability of arbitrary sparse signals under erasures has been studied in compressed sensing.