WeatherFormer: A Pretrained Encoder Model for Learning Robust Weather Representations from Small Datasets

This paper introduces WeatherFormer, a transformer encoder-based model designed to learn robust weather features from minimal observations. It addresses the challenge of modeling complex weather dynamics from small datasets, a bottleneck for many prediction tasks in agriculture, epidemiology, and climate science. WeatherFormer was pretrained on a large pretraining dataset comprised of 39 years of satellite measurements across the Americas. With a novel pretraining task and fine-tuning, WeatherFormer achieves state-of-the-art performance in county-level soybean yield prediction and influenza forecasting. Technical innovations include a unique spatiotemporal encoding that captures geographical, annual, and seasonal variations, adapting the transformer architecture to continuous weather data, and a pretraining strategy to learn representations that are robust to missing weather features. This paper for the first time demonstrates the effectiveness of pretraining large transformer encoder models for weather-dependent applications across multiple domains.

Sample Efficient Reinforcement Learning with Partial Dynamics Knowledge

The problem of sample complexity of online reinforcement learning is often studied in the literature without taking into account any partial knowledge about the system dynamics that could potentially accelerate the learning process. In this paper, we study the sample complexity of online Q-learning methods when some prior knowledge about the dynamics is available or can be learned efficiently. We focus on systems that evolve according to an additive disturbance model of the form $S_{h+1} = f(S_h, A_h) + W_h$, where $f$ represents the underlying system dynamics, and $W_h$ are unknown disturbances independent of states and actions. In the setting of finite episodic Markov decision processes with $S$ states, $A$ actions, and episode length $H$, we present an optimistic Q-learning algorithm that achieves $\tilde{\mathcal{O}}(\text{Poly}(H)\sqrt{T})$ regret under perfect knowledge of $f$, where $T$ is the total number of interactions with the system. This is in contrast to the typical $\tilde{\mathcal{O}}(\text{Poly}(H)\sqrt{SAT})$ regret for existing Q-learning methods. Further, if only a noisy estimate $\hat{f}$ of $f$ is available, our method can learn an approximately optimal policy in a number of samples that is independent of the cardinalities of state and action spaces. The sub-optimality gap depends on the approximation error $\hat{f}-f$, as well as the Lipschitz constant of the corresponding optimal value function. Our approach does not require modeling of the transition probabilities and enjoys the same memory complexity as model-free methods.

Estimation of Models with Limited Data by Leveraging Shared Structure

Modern data sets, such as those in healthcare and e-commerce, are often derived from many individuals or systems but have insufficient data from each source alone to separately estimate individual, often high-dimensional, model parameters. If there is shared structure among systems however, it may be possible to leverage data from other systems to help estimate individual parameters, which could otherwise be non-identifiable. In this paper, we assume systems share a latent low-dimensional parameter space and propose a method for recovering $d$-dimensional parameters for $N$ different linear systems, even when there are only $T<d$ observations per system. To do so, we develop a three-step algorithm which estimates the low-dimensional subspace spanned by the systems' parameters and produces refined parameter estimates within the subspace. We provide finite sample subspace estimation error guarantees for our proposed method. Finally, we experimentally validate our method on simulations with i.i.d. regression data and as well as correlated time series data.

SAMoSSA: Multivariate Singular Spectrum Analysis with Stochastic Autoregressive Noise

The well-established practice of time series analysis involves estimating deterministic, non-stationary trend and seasonality components followed by learning the residual stochastic, stationary components. Recently, it has been shown that one can learn the deterministic non-stationary components accurately using multivariate Singular Spectrum Analysis (mSSA) in the absence of a correlated stationary component; meanwhile, in the absence of deterministic non-stationary components, the Autoregressive (AR) stationary component can also be learnt readily, e.g. via Ordinary Least Squares (OLS). However, a theoretical underpinning of multi-stage learning algorithms involving both deterministic and stationary components has been absent in the literature despite its pervasiveness. We resolve this open question by establishing desirable theoretical guarantees for a natural two-stage algorithm, where mSSA is first applied to estimate the non-stationary components despite the presence of a correlated stationary AR component, which is subsequently learned from the residual time series. We provide a finite-sample forecasting consistency bound for the proposed algorithm, SAMoSSA, which is data-driven and thus requires minimal parameter tuning. To establish theoretical guarantees, we overcome three hurdles: (i) we characterize the spectra of Page matrices of stable AR processes, thus extending the analysis of mSSA; (ii) we extend the analysis of AR process identification in the presence of arbitrary bounded perturbations; (iii) we characterize the out-of-sample or forecasting error, as opposed to solely considering model identification. Through representative empirical studies, we validate the superior performance of SAMoSSA compared to existing baselines. Notably, SAMoSSA's ability to account for AR noise structure yields improvements ranging from 5% to 37% across various benchmark datasets.

Causal Matrix Completion

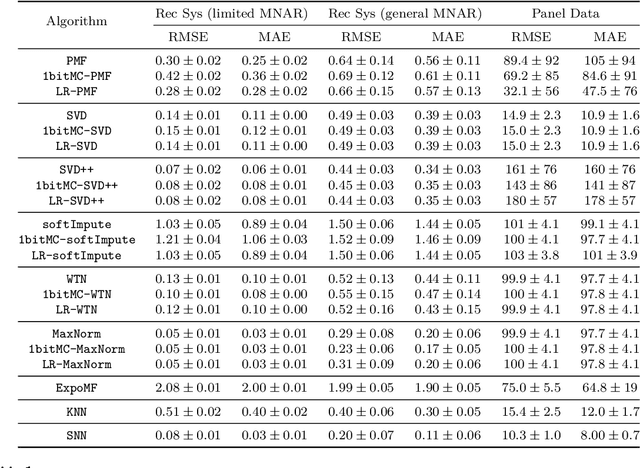
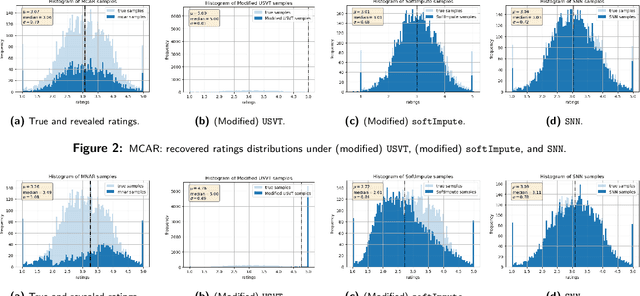
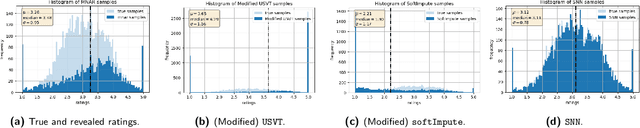
Matrix completion is the study of recovering an underlying matrix from a sparse subset of noisy observations. Traditionally, it is assumed that the entries of the matrix are "missing completely at random" (MCAR), i.e., each entry is revealed at random, independent of everything else, with uniform probability. This is likely unrealistic due to the presence of "latent confounders", i.e., unobserved factors that determine both the entries of the underlying matrix and the missingness pattern in the observed matrix. For example, in the context of movie recommender systems -- a canonical application for matrix completion -- a user who vehemently dislikes horror films is unlikely to ever watch horror films. In general, these confounders yield "missing not at random" (MNAR) data, which can severely impact any inference procedure that does not correct for this bias. We develop a formal causal model for matrix completion through the language of potential outcomes, and provide novel identification arguments for a variety of causal estimands of interest. We design a procedure, which we call "synthetic nearest neighbors" (SNN), to estimate these causal estimands. We prove finite-sample consistency and asymptotic normality of our estimator. Our analysis also leads to new theoretical results for the matrix completion literature. In particular, we establish entry-wise, i.e., max-norm, finite-sample consistency and asymptotic normality results for matrix completion with MNAR data. As a special case, this also provides entry-wise bounds for matrix completion with MCAR data. Across simulated and real data, we demonstrate the efficacy of our proposed estimator.

Minimal Realization Problems for Hidden Markov Models

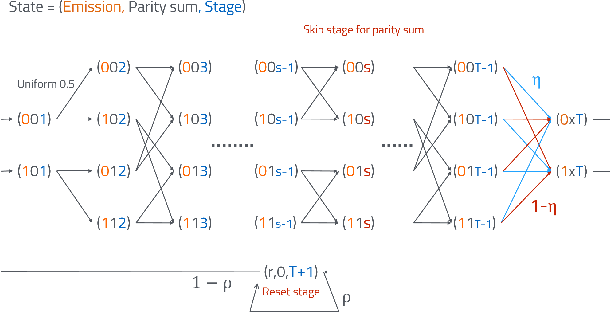
Consider a stationary discrete random process with alphabet size d, which is assumed to be the output process of an unknown stationary Hidden Markov Model (HMM). Given the joint probabilities of finite length strings of the process, we are interested in finding a finite state generative model to describe the entire process. In particular, we focus on two classes of models: HMMs and quasi-HMMs, which is a strictly larger class of models containing HMMs. In the main theorem, we show that if the random process is generated by an HMM of order less or equal than k, and whose transition and observation probability matrix are in general position, namely almost everywhere on the parameter space, both the minimal quasi-HMM realization and the minimal HMM realization can be efficiently computed based on the joint probabilities of all the length N strings, for N > 4 lceil log_d(k) rceil +1. In this paper, we also aim to compare and connect the two lines of literature: realization theory of HMMs, and the recent development in learning latent variable models with tensor decomposition techniques.