Supervised learning pays attention

In-context learning with attention enables large neural networks to make context-specific predictions by selectively focusing on relevant examples. Here, we adapt this idea to supervised learning procedures such as lasso regression and gradient boosting, for tabular data. Our goals are to (1) flexibly fit personalized models for each prediction point and (2) retain model simplicity and interpretability. Our method fits a local model for each test observation by weighting the training data according to attention, a supervised similarity measure that emphasizes features and interactions that are predictive of the outcome. Attention weighting allows the method to adapt to heterogeneous data in a data-driven way, without requiring cluster or similarity pre-specification. Further, our approach is uniquely interpretable: for each test observation, we identify which features are most predictive and which training observations are most relevant. We then show how to use attention weighting for time series and spatial data, and we present a method for adapting pretrained tree-based models to distributional shift using attention-weighted residual corrections. Across real and simulated datasets, attention weighting improves predictive performance while preserving interpretability, and theory shows that attention-weighting linear models attain lower mean squared error than the standard linear model under mixture-of-models data-generating processes with known subgroup structure.

Lassoed Forests: Random Forests with Adaptive Lasso Post-selection

Random forests are a statistical learning technique that use bootstrap aggregation to average high-variance and low-bias trees. Improvements to random forests, such as applying Lasso regression to the tree predictions, have been proposed in order to reduce model bias. However, these changes can sometimes degrade performance (e.g., an increase in mean squared error). In this paper, we show in theory that the relative performance of these two methods, standard and Lasso-weighted random forests, depends on the signal-to-noise ratio. We further propose a unified framework to combine random forests and Lasso selection by applying adaptive weighting and show mathematically that it can strictly outperform the other two methods. We compare the three methods through simulation, including bias-variance decomposition, error estimates evaluation, and variable importance analysis. We also show the versatility of our method by applications to a variety of real-world datasets.

Pre-validation Revisited

Pre-validation is a way to build prediction model with two datasets of significantly different feature dimensions. Previous work showed that the asymptotic distribution of test statistic for the pre-validated predictor deviated from a standard Normal, hence will lead to issues in hypothesis tests. In this paper, we revisited the pre-validation procedure and extended the problem formulation without any independence assumption on the two feature sets. We proposed not only an analytical distribution of the test statistics for pre-validated predictor under certain models, but also a generic bootstrap procedure to conduct inference. We showed properties and benefits of pre-validation in prediction, inference and error estimation by simulation and various applications, including analysis of a breast cancer study and a synthetic GWAS example.

Statistical Learning for Heterogeneous Treatment Effects: Pretraining, Prognosis, and Prediction

Robust estimation of heterogeneous treatment effects is a fundamental challenge for optimal decision-making in domains ranging from personalized medicine to educational policy. In recent years, predictive machine learning has emerged as a valuable toolbox for causal estimation, enabling more flexible effect estimation. However, accurately estimating conditional average treatment effects (CATE) remains a major challenge, particularly in the presence of many covariates. In this article, we propose pretraining strategies that leverages a phenomenon in real-world applications: factors that are prognostic of the outcome are frequently also predictive of treatment effect heterogeneity. In medicine, for example, components of the same biological signaling pathways frequently influence both baseline risk and treatment response. Specifically, we demonstrate our approach within the R-learner framework, which estimates the CATE by solving individual prediction problems based on a residualized loss. We use this structure to incorporate "side information" and develop models that can exploit synergies between risk prediction and causal effect estimation. In settings where these synergies are present, this cross-task learning enables more accurate signal detection: yields lower estimation error, reduced false discovery rates, and higher power for detecting heterogeneity.

BIOMEDICA: An Open Biomedical Image-Caption Archive, Dataset, and Vision-Language Models Derived from Scientific Literature

The development of vision-language models (VLMs) is driven by large-scale and diverse multimodal datasets. However, progress toward generalist biomedical VLMs is limited by the lack of annotated, publicly accessible datasets across biology and medicine. Existing efforts are restricted to narrow domains, missing the full diversity of biomedical knowledge encoded in scientific literature. To address this gap, we introduce BIOMEDICA, a scalable, open-source framework to extract, annotate, and serialize the entirety of the PubMed Central Open Access subset into an easy-to-use, publicly accessible dataset. Our framework produces a comprehensive archive with over 24 million unique image-text pairs from over 6 million articles. Metadata and expert-guided annotations are also provided. We demonstrate the utility and accessibility of our resource by releasing BMCA-CLIP, a suite of CLIP-style models continuously pre-trained on the BIOMEDICA dataset via streaming, eliminating the need to download 27 TB of data locally. On average, our models achieve state-of-the-art performance across 40 tasks - spanning pathology, radiology, ophthalmology, dermatology, surgery, molecular biology, parasitology, and cell biology - excelling in zero-shot classification with a 6.56% average improvement (as high as 29.8% and 17.5% in dermatology and ophthalmology, respectively), and stronger image-text retrieval, all while using 10x less compute. To foster reproducibility and collaboration, we release our codebase and dataset for the broader research community.

Semiparametric conformal prediction

Many risk-sensitive applications require well-calibrated prediction sets over multiple, potentially correlated target variables, for which the prediction algorithm may report correlated non-conformity scores. In this work, we treat the scores as random vectors and aim to construct the prediction set accounting for their joint correlation structure. Drawing from the rich literature on multivariate quantiles and semiparametric statistics, we propose an algorithm to estimate the $1-\alpha$ quantile of the scores, where $\alpha$ is the user-specified miscoverage rate. In particular, we flexibly estimate the joint cumulative distribution function (CDF) of the scores using nonparametric vine copulas and improve the asymptotic efficiency of the quantile estimate using its influence function. The vine decomposition allows our method to scale well to a large number of targets. We report desired coverage and competitive efficiency on a range of real-world regression problems, including those with missing-at-random labels in the calibration set.

MMIL: A novel algorithm for disease associated cell type discovery

Single-cell datasets often lack individual cell labels, making it challenging to identify cells associated with disease. To address this, we introduce Mixture Modeling for Multiple Instance Learning (MMIL), an expectation maximization method that enables the training and calibration of cell-level classifiers using patient-level labels. Our approach can be used to train e.g. lasso logistic regression models, gradient boosted trees, and neural networks. When applied to clinically-annotated, primary patient samples in Acute Myeloid Leukemia (AML) and Acute Lymphoblastic Leukemia (ALL), our method accurately identifies cancer cells, generalizes across tissues and treatment timepoints, and selects biologically relevant features. In addition, MMIL is capable of incorporating cell labels into model training when they are known, providing a powerful framework for leveraging both labeled and unlabeled data simultaneously. Mixture Modeling for MIL offers a novel approach for cell classification, with significant potential to advance disease understanding and management, especially in scenarios with unknown gold-standard labels and high dimensionality.

Using Pre-training and Interaction Modeling for ancestry-specific disease prediction in UK Biobank

Recent genome-wide association studies (GWAS) have uncovered the genetic basis of complex traits, but show an under-representation of non-European descent individuals, underscoring a critical gap in genetic research. Here, we assess whether we can improve disease prediction across diverse ancestries using multiomic data. We evaluate the performance of Group-LASSO INTERaction-NET (glinternet) and pretrained lasso in disease prediction focusing on diverse ancestries in the UK Biobank. Models were trained on data from White British and other ancestries and validated across a cohort of over 96,000 individuals for 8 diseases. Out of 96 models trained, we report 16 with statistically significant incremental predictive performance in terms of ROC-AUC scores. These findings suggest that advanced statistical methods that borrow information across multiple ancestries may improve disease risk prediction, but with limited benefit.

FastCPH: Efficient Survival Analysis for Neural Networks

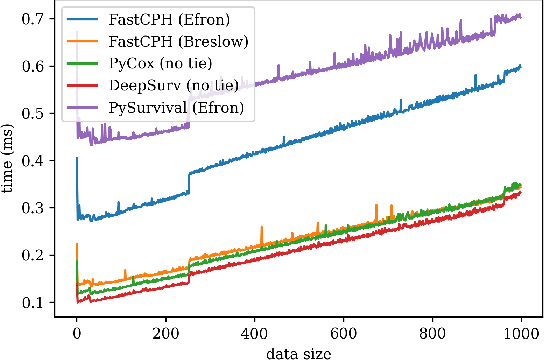
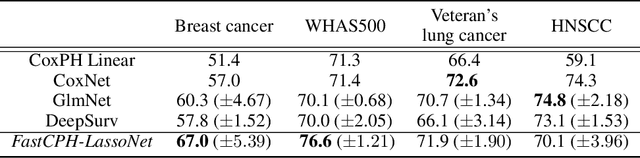
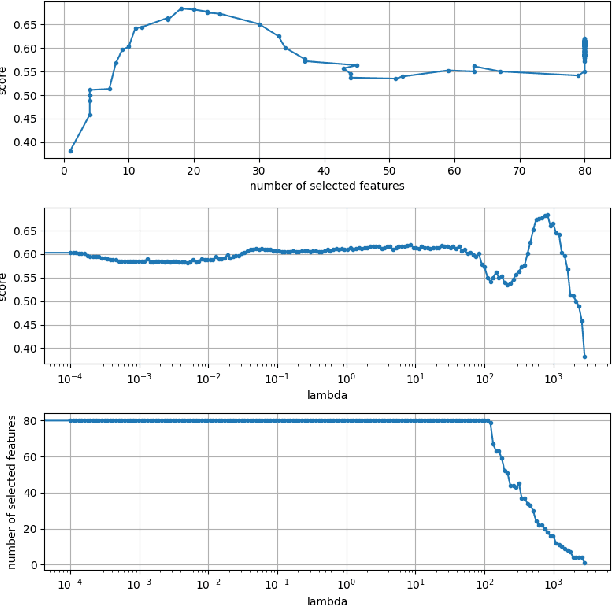
The Cox proportional hazards model is a canonical method in survival analysis for prediction of the life expectancy of a patient given clinical or genetic covariates -- it is a linear model in its original form. In recent years, several methods have been proposed to generalize the Cox model to neural networks, but none of these are both numerically correct and computationally efficient. We propose FastCPH, a new method that runs in linear time and supports both the standard Breslow and Efron methods for tied events. We also demonstrate the performance of FastCPH combined with LassoNet, a neural network that provides interpretability through feature sparsity, on survival datasets. The final procedure is efficient, selects useful covariates and outperforms existing CoxPH approaches.

Confidence intervals for the Cox model test error from cross-validation

Cross-validation (CV) is one of the most widely used techniques in statistical learning for estimating the test error of a model, but its behavior is not yet fully understood. It has been shown that standard confidence intervals for test error using estimates from CV may have coverage below nominal levels. This phenomenon occurs because each sample is used in both the training and testing procedures during CV and as a result, the CV estimates of the errors become correlated. Without accounting for this correlation, the estimate of the variance is smaller than it should be. One way to mitigate this issue is by estimating the mean squared error of the prediction error instead using nested CV. This approach has been shown to achieve superior coverage compared to intervals derived from standard CV. In this work, we generalize the nested CV idea to the Cox proportional hazards model and explore various choices of test error for this setting.