Semiparametric conformal prediction

Many risk-sensitive applications require well-calibrated prediction sets over multiple, potentially correlated target variables, for which the prediction algorithm may report correlated non-conformity scores. In this work, we treat the scores as random vectors and aim to construct the prediction set accounting for their joint correlation structure. Drawing from the rich literature on multivariate quantiles and semiparametric statistics, we propose an algorithm to estimate the $1-\alpha$ quantile of the scores, where $\alpha$ is the user-specified miscoverage rate. In particular, we flexibly estimate the joint cumulative distribution function (CDF) of the scores using nonparametric vine copulas and improve the asymptotic efficiency of the quantile estimate using its influence function. The vine decomposition allows our method to scale well to a large number of targets. We report desired coverage and competitive efficiency on a range of real-world regression problems, including those with missing-at-random labels in the calibration set.

Blind Biological Sequence Denoising with Self-Supervised Set Learning

Biological sequence analysis relies on the ability to denoise the imprecise output of sequencing platforms. We consider a common setting where a short sequence is read out repeatedly using a high-throughput long-read platform to generate multiple subreads, or noisy observations of the same sequence. Denoising these subreads with alignment-based approaches often fails when too few subreads are available or error rates are too high. In this paper, we propose a novel method for blindly denoising sets of sequences without directly observing clean source sequence labels. Our method, Self-Supervised Set Learning (SSSL), gathers subreads together in an embedding space and estimates a single set embedding as the midpoint of the subreads in both the latent and sequence spaces. This set embedding represents the "average" of the subreads and can be decoded into a prediction of the clean sequence. In experiments on simulated long-read DNA data, SSSL methods denoise small reads of $\leq 6$ subreads with 17% fewer errors and large reads of $>6$ subreads with 8% fewer errors compared to the best baseline. On a real dataset of antibody sequences, SSSL improves over baselines on two self-supervised metrics, with a significant improvement on difficult small reads that comprise over 60% of the test set. By accurately denoising these reads, SSSL promises to better realize the potential of high-throughput DNA sequencing data for downstream scientific applications.

BOtied: Multi-objective Bayesian optimization with tied multivariate ranks

Many scientific and industrial applications require joint optimization of multiple, potentially competing objectives. Multi-objective Bayesian optimization (MOBO) is a sample-efficient framework for identifying Pareto-optimal solutions. We show a natural connection between non-dominated solutions and the highest multivariate rank, which coincides with the outermost level line of the joint cumulative distribution function (CDF). We propose the CDF indicator, a Pareto-compliant metric for evaluating the quality of approximate Pareto sets that complements the popular hypervolume indicator. At the heart of MOBO is the acquisition function, which determines the next candidate to evaluate by navigating the best compromises among the objectives. Multi-objective acquisition functions that rely on box decomposition of the objective space, such as the expected hypervolume improvement (EHVI) and entropy search, scale poorly to a large number of objectives. We propose an acquisition function, called BOtied, based on the CDF indicator. BOtied can be implemented efficiently with copulas, a statistical tool for modeling complex, high-dimensional distributions. We benchmark BOtied against common acquisition functions, including EHVI and random scalarization (ParEGO), in a series of synthetic and real-data experiments. BOtied performs on par with the baselines across datasets and metrics while being computationally efficient.

Chain of Log-Concave Markov Chains

Markov chain Monte Carlo (MCMC) is a class of general-purpose algorithms for sampling from unnormalized densities. There are two well-known problems facing MCMC in high dimensions: (i) The distributions of interest are concentrated in pockets separated by large regions with small probability mass, and (ii) The log-concave pockets themselves are typically ill-conditioned. We introduce a framework to tackle these problems using isotropic Gaussian smoothing. We prove one can always decompose sampling from a density (minimal assumptions made on the density) into a sequence of sampling from log-concave conditional densities via accumulation of noisy measurements with equal noise levels. This construction keeps track of a history of samples, making it non-Markovian as a whole, but the history only shows up in the form of an empirical mean, making the memory footprint minimal. Our sampling algorithm generalizes walk-jump sampling [1]. The "walk" phase becomes a (non-Markovian) chain of log-concave Langevin chains. The "jump" from the accumulated measurements is obtained by empirical Bayes. We study our sampling algorithm quantitatively using the 2-Wasserstein metric and compare it with various Langevin MCMC algorithms. We also report a remarkable capacity of our algorithm to "tunnel" between modes of a distribution.

SupSiam: Non-contrastive Auxiliary Loss for Learning from Molecular Conformers

We investigate Siamese networks for learning related embeddings for augmented samples of molecular conformers. We find that a non-contrastive (positive-pair only) auxiliary task aids in supervised training of Euclidean neural networks (E3NNs) and increases manifold smoothness (MS) around point-cloud geometries. We demonstrate this property for multiple drug-activity prediction tasks while maintaining relevant performance metrics, and propose an extension of MS to probabilistic and regression settings. We provide an analysis of representation collapse, finding substantial effects of task-weighting, latent dimension, and regularization. We expect the presented protocol to aid in the development of reliable E3NNs from molecular conformers, even for small-data drug discovery programs.

Hierarchical Inference of the Lensing Convergence from Photometric Catalogs with Bayesian Graph Neural Networks

We present a Bayesian graph neural network (BGNN) that can estimate the weak lensing convergence ($\kappa$) from photometric measurements of galaxies along a given line of sight. The method is of particular interest in strong gravitational time delay cosmography (TDC), where characterizing the "external convergence" ($\kappa_{\rm ext}$) from the lens environment and line of sight is necessary for precise inference of the Hubble constant ($H_0$). Starting from a large-scale simulation with a $\kappa$ resolution of $\sim$1$'$, we introduce fluctuations on galaxy-galaxy lensing scales of $\sim$1$''$ and extract random sightlines to train our BGNN. We then evaluate the model on test sets with varying degrees of overlap with the training distribution. For each test set of 1,000 sightlines, the BGNN infers the individual $\kappa$ posteriors, which we combine in a hierarchical Bayesian model to yield constraints on the hyperparameters governing the population. For a test field well sampled by the training set, the BGNN recovers the population mean of $\kappa$ precisely and without bias, resulting in a contribution to the $H_0$ error budget well under 1\%. In the tails of the training set with sparse samples, the BGNN, which can ingest all available information about each sightline, extracts more $\kappa$ signal compared to a simplified version of the traditional method based on matching galaxy number counts, which is limited by sample variance. Our hierarchical inference pipeline using BGNNs promises to improve the $\kappa_{\rm ext}$ characterization for precision TDC. The implementation of our pipeline is available as a public Python package, Node to Joy.

PropertyDAG: Multi-objective Bayesian optimization of partially ordered, mixed-variable properties for biological sequence design

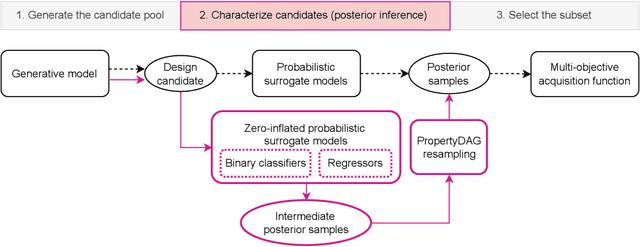
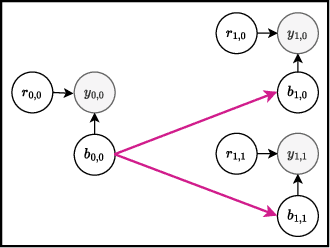
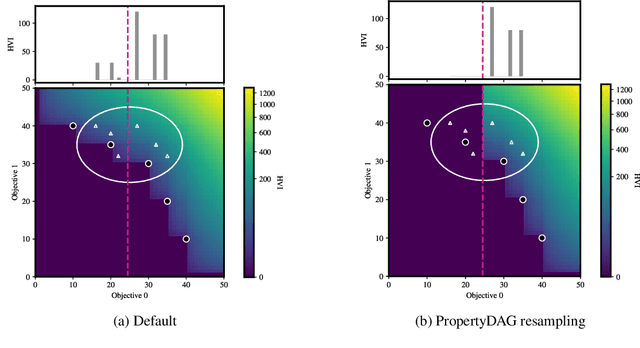
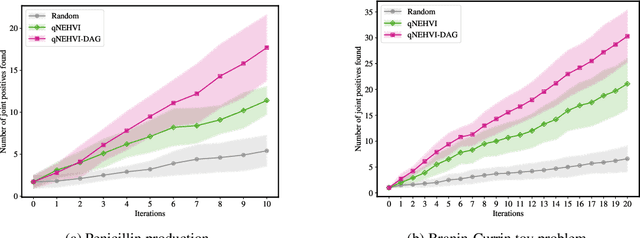
Bayesian optimization offers a sample-efficient framework for navigating the exploration-exploitation trade-off in the vast design space of biological sequences. Whereas it is possible to optimize the various properties of interest jointly using a multi-objective acquisition function, such as the expected hypervolume improvement (EHVI), this approach does not account for objectives with a hierarchical dependency structure. We consider a common use case where some regions of the Pareto frontier are prioritized over others according to a specified $\textit{partial ordering}$ in the objectives. For instance, when designing antibodies, we would like to maximize the binding affinity to a target antigen only if it can be expressed in live cell culture -- modeling the experimental dependency in which affinity can only be measured for antibodies that can be expressed and thus produced in viable quantities. In general, we may want to confer a partial ordering to the properties such that each property is optimized conditioned on its parent properties satisfying some feasibility condition. To this end, we present PropertyDAG, a framework that operates on top of the traditional multi-objective BO to impose this desired ordering on the objectives, e.g. expression $\rightarrow$ affinity. We demonstrate its performance over multiple simulated active learning iterations on a penicillin production task, toy numerical problem, and a real-world antibody design task.

Multi-segment preserving sampling for deep manifold sampler

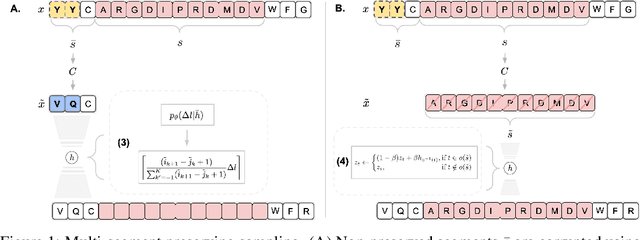
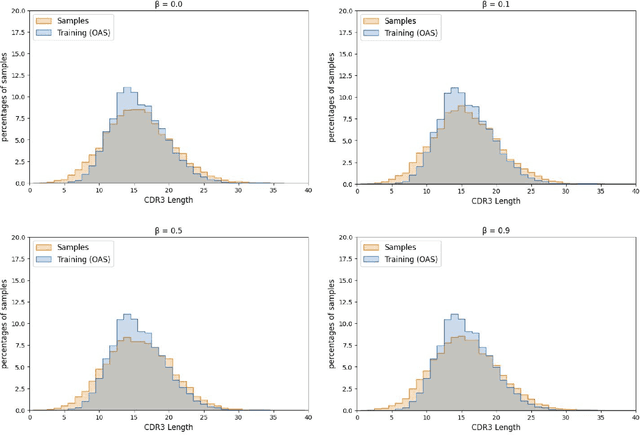
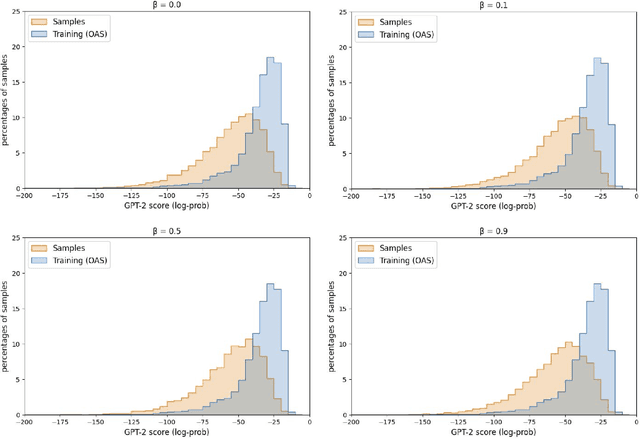
Deep generative modeling for biological sequences presents a unique challenge in reconciling the bias-variance trade-off between explicit biological insight and model flexibility. The deep manifold sampler was recently proposed as a means to iteratively sample variable-length protein sequences by exploiting the gradients from a function predictor. We introduce an alternative approach to this guided sampling procedure, multi-segment preserving sampling, that enables the direct inclusion of domain-specific knowledge by designating preserved and non-preserved segments along the input sequence, thereby restricting variation to only select regions. We present its effectiveness in the context of antibody design by training two models: a deep manifold sampler and a GPT-2 language model on nearly six million heavy chain sequences annotated with the IGHV1-18 gene. During sampling, we restrict variation to only the complementarity-determining region 3 (CDR3) of the input. We obtain log probability scores from a GPT-2 model for each sampled CDR3 and demonstrate that multi-segment preserving sampling generates reasonable designs while maintaining the desired, preserved regions.

Inferring Black Hole Properties from Astronomical Multivariate Time Series with Bayesian Attentive Neural Processes

Among the most extreme objects in the Universe, active galactic nuclei (AGN) are luminous centers of galaxies where a black hole feeds on surrounding matter. The variability patterns of the light emitted by an AGN contain information about the physical properties of the underlying black hole. Upcoming telescopes will observe over 100 million AGN in multiple broadband wavelengths, yielding a large sample of multivariate time series with long gaps and irregular sampling. We present a method that reconstructs the AGN time series and simultaneously infers the posterior probability density distribution (PDF) over the physical quantities of the black hole, including its mass and luminosity. We apply this method to a simulated dataset of 11,000 AGN and report precision and accuracy of 0.4 dex and 0.3 dex in the inferred black hole mass. This work is the first to address probabilistic time series reconstruction and parameter inference for AGN in an end-to-end fashion.

Large-Scale Gravitational Lens Modeling with Bayesian Neural Networks for Accurate and Precise Inference of the Hubble Constant

We investigate the use of approximate Bayesian neural networks (BNNs) in modeling hundreds of time-delay gravitational lenses for Hubble constant ($H_0$) determination. Our BNN was trained on synthetic HST-quality images of strongly lensed active galactic nuclei (AGN) with lens galaxy light included. The BNN can accurately characterize the posterior PDFs of model parameters governing the elliptical power-law mass profile in an external shear field. We then propagate the BNN-inferred posterior PDFs into ensemble $H_0$ inference, using simulated time delay measurements from a plausible dedicated monitoring campaign. Assuming well-measured time delays and a reasonable set of priors on the environment of the lens, we achieve a median precision of $9.3$\% per lens in the inferred $H_0$. A simple combination of 200 test-set lenses results in a precision of 0.5 $\textrm{km s}^{-1} \textrm{ Mpc}^{-1}$ ($0.7\%$), with no detectable bias in this $H_0$ recovery test. The computation time for the entire pipeline -- including the training set generation, BNN training, and $H_0$ inference -- translates to 9 minutes per lens on average for 200 lenses and converges to 6 minutes per lens as the sample size is increased. Being fully automated and efficient, our pipeline is a promising tool for exploring ensemble-level systematics in lens modeling for $H_0$ inference.