Prompt Selection Matters: Enhancing Text Annotations for Social Sciences with Large Language Models

Large Language Models have recently been applied to text annotation tasks from social sciences, equalling or surpassing the performance of human workers at a fraction of the cost. However, no inquiry has yet been made on the impact of prompt selection on labelling accuracy. In this study, we show that performance greatly varies between prompts, and we apply the method of automatic prompt optimization to systematically craft high quality prompts. We also provide the community with a simple, browser-based implementation of the method at https://prompt-ultra.github.io/ .

FastCPH: Efficient Survival Analysis for Neural Networks

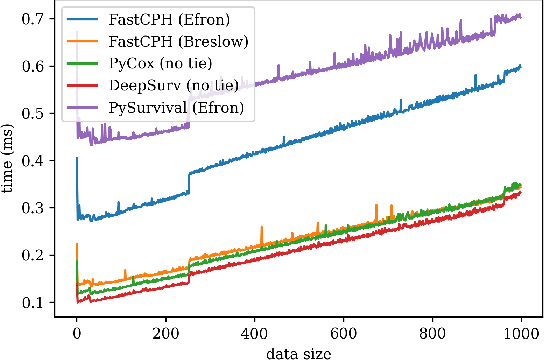
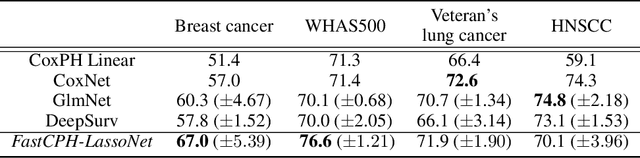
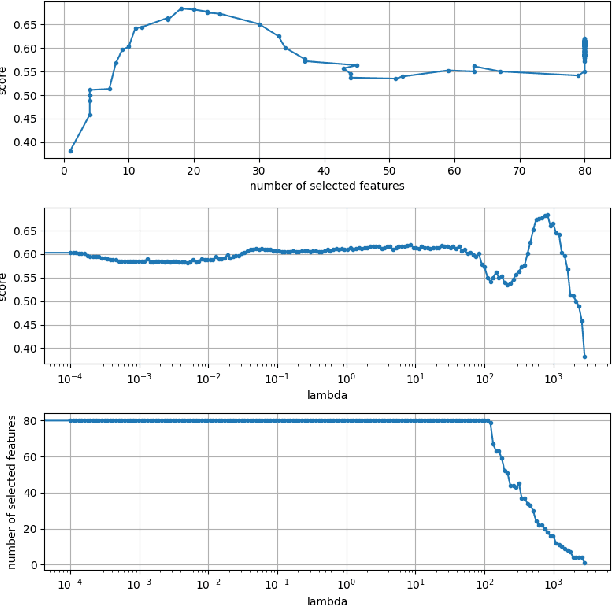
The Cox proportional hazards model is a canonical method in survival analysis for prediction of the life expectancy of a patient given clinical or genetic covariates -- it is a linear model in its original form. In recent years, several methods have been proposed to generalize the Cox model to neural networks, but none of these are both numerically correct and computationally efficient. We propose FastCPH, a new method that runs in linear time and supports both the standard Breslow and Efron methods for tied events. We also demonstrate the performance of FastCPH combined with LassoNet, a neural network that provides interpretability through feature sparsity, on survival datasets. The final procedure is efficient, selects useful covariates and outperforms existing CoxPH approaches.

Competition analysis on the over-the-counter credit default swap market

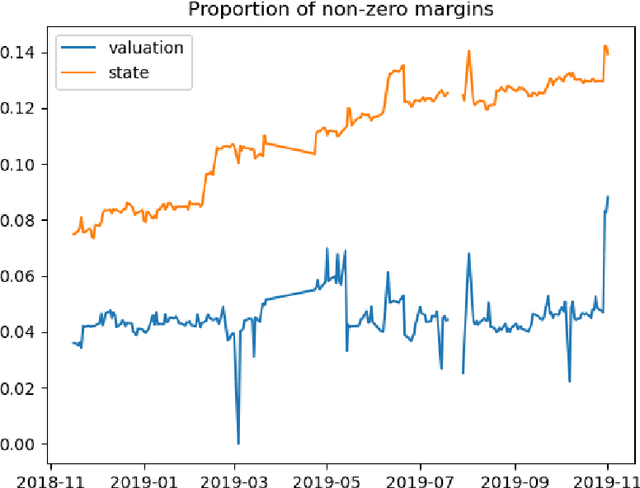
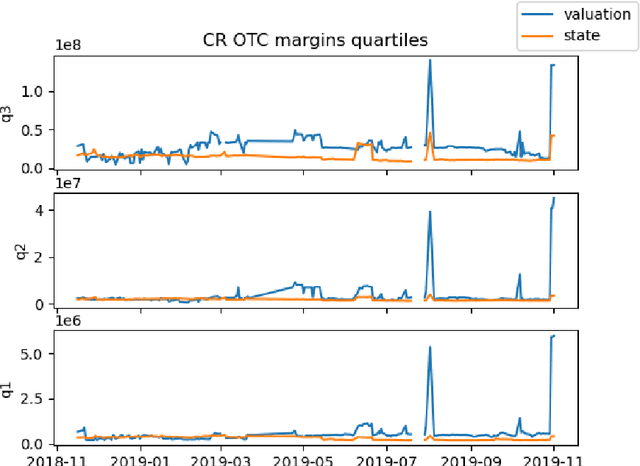
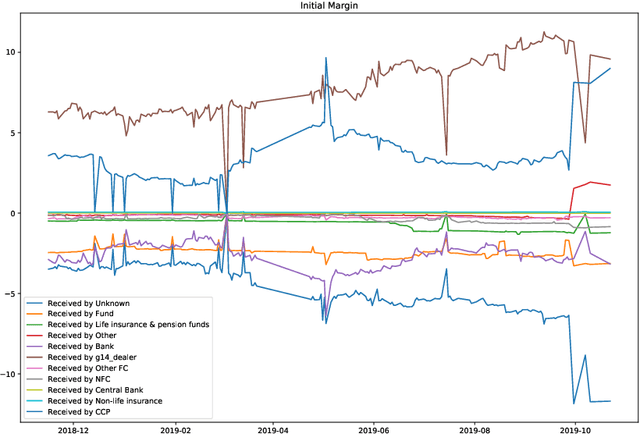
We study two questions related to competition on the OTC CDS market using data collected as part of the EMIR regulation. First, we study the competition between central counterparties through collateral requirements. We present models that successfully estimate the initial margin requirements. However, our estimations are not precise enough to use them as input to a predictive model for CCP choice by counterparties in the OTC market. Second, we model counterpart choice on the interdealer market using a novel semi-supervised predictive task. We present our methodology as part of the literature on model interpretability before arguing for the use of conditional entropy as the metric of interest to derive knowledge from data through a model-agnostic approach. In particular, we justify the use of deep neural networks to measure conditional entropy on real-world datasets. We create the $\textit{Razor entropy}$ using the framework of algorithmic information theory and derive an explicit formula that is identical to our semi-supervised training objective. Finally, we borrow concepts from game theory to define $\textit{top-k Shapley values}$. This novel method of payoff distribution satisfies most of the properties of Shapley values, and is of particular interest when the value function is monotone submodular. Unlike classical Shapley values, top-k Shapley values can be computed in quadratic time of the number of features instead of exponential. We implement our methodology and report the results on our particular task of counterpart choice. Finally, we present an improvement to the $\textit{node2vec}$ algorithm that could for example be used to further study intermediation. We show that the neighbor sampling used in the generation of biased walks can be performed in logarithmic time with a quasilinear time pre-computation, unlike the current implementations that do not scale well.

Bloom Origami Assays: Practical Group Testing

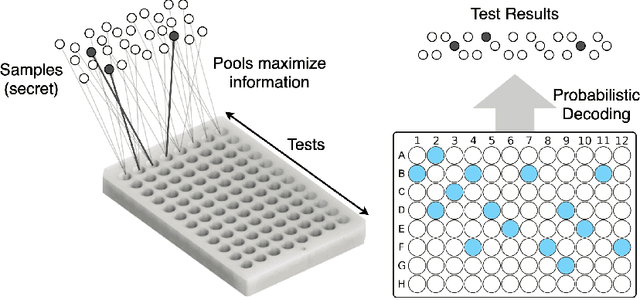
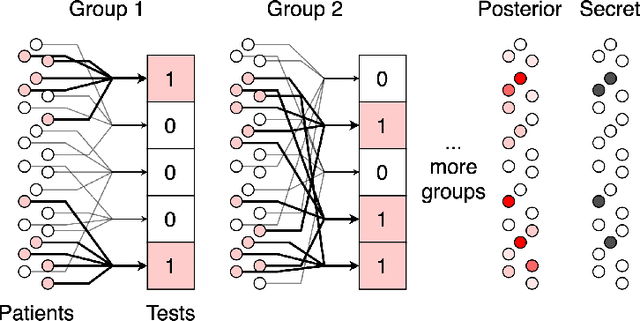
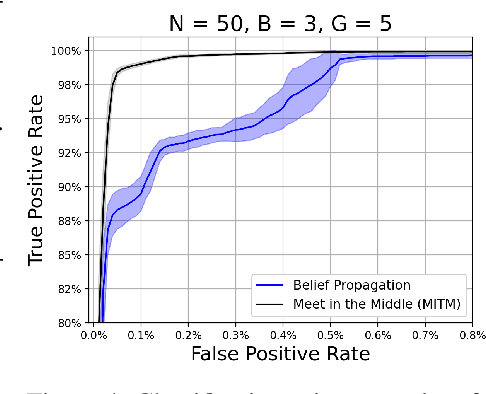
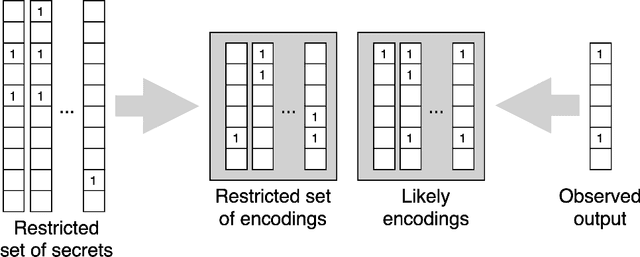
We study the problem usually referred to as group testing in the context of COVID-19. Given n samples collected from patients, how should we select and test mixtures of samples to maximize information and minimize the number of tests? Group testing is a well-studied problem with several appealing solutions, but recent biological studies impose practical constraints for COVID-19 that are incompatible with traditional methods. Furthermore, existing methods use unnecessarily restrictive solutions, which were devised for settings with more memory and compute constraints than the problem at hand. This results in poor utility. In the new setting, we obtain strong solutions for small values of n using evolutionary strategies. We then develop a new method combining Bloom filters with belief propagation to scale to larger values of n (more than 100) with good empirical results. We also present a more accurate decoding algorithm that is tailored for specific COVID-19 settings. This work demonstrates the practical gap between dedicated algorithms and well-known generic solutions. Our efforts results in a new and practical multiplex method yielding strong empirical performance without mixing more than a chosen number of patients into the same probe. Finally, we briefly discuss adaptive methods, casting them into the framework of adaptive sub-modularity.

Crackovid: Optimizing Group Testing

We study the problem usually referred to as group testing in the context of COVID-19. Given $n$ samples taken from patients, how should we select mixtures of samples to be tested, so as to maximize information and minimize the number of tests? We consider both adaptive and non-adaptive strategies, and take a Bayesian approach with a prior both for infection of patients and test errors. We start by proposing a mathematically principled objective, grounded in information theory. We then optimize non-adaptive optimization strategies using genetic algorithms, and leverage the mathematical framework of adaptive sub-modularity to obtain theoretical guarantees for the greedy-adaptive method.