Statistical Learning for Heterogeneous Treatment Effects: Pretraining, Prognosis, and Prediction

Robust estimation of heterogeneous treatment effects is a fundamental challenge for optimal decision-making in domains ranging from personalized medicine to educational policy. In recent years, predictive machine learning has emerged as a valuable toolbox for causal estimation, enabling more flexible effect estimation. However, accurately estimating conditional average treatment effects (CATE) remains a major challenge, particularly in the presence of many covariates. In this article, we propose pretraining strategies that leverages a phenomenon in real-world applications: factors that are prognostic of the outcome are frequently also predictive of treatment effect heterogeneity. In medicine, for example, components of the same biological signaling pathways frequently influence both baseline risk and treatment response. Specifically, we demonstrate our approach within the R-learner framework, which estimates the CATE by solving individual prediction problems based on a residualized loss. We use this structure to incorporate "side information" and develop models that can exploit synergies between risk prediction and causal effect estimation. In settings where these synergies are present, this cross-task learning enables more accurate signal detection: yields lower estimation error, reduced false discovery rates, and higher power for detecting heterogeneity.

Proximal Causal Learning of Heterogeneous Treatment Effects

Efficiently and flexibly estimating treatment effect heterogeneity is an important task in a wide variety of settings ranging from medicine to marketing, and there are a considerable number of promising conditional average treatment effect estimators currently available. These, however, typically rely on the assumption that the measured covariates are enough to justify conditional exchangeability. We propose the P-learner, motivated by the R-learner, a tailored two-stage loss function for learning heterogeneous treatment effects in settings where exchangeability given observed covariates is an implausible assumption, and we wish to rely on proxy variables for causal inference. Our proposed estimator can be implemented by off-the-shelf loss-minimizing machine learning methods, which in the case of kernel regression satisfies an oracle bound on the estimated error as long as the nuisance components are estimated reasonably well.

What Makes Forest-Based Heterogeneous Treatment Effect Estimators Work?

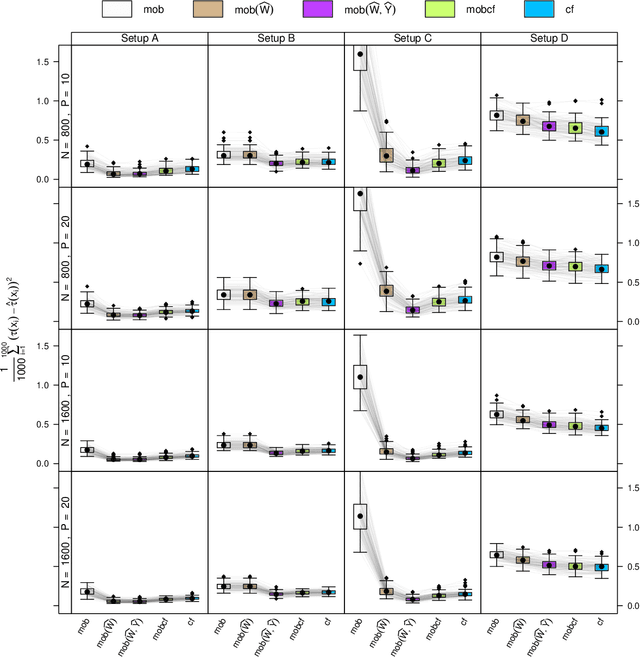
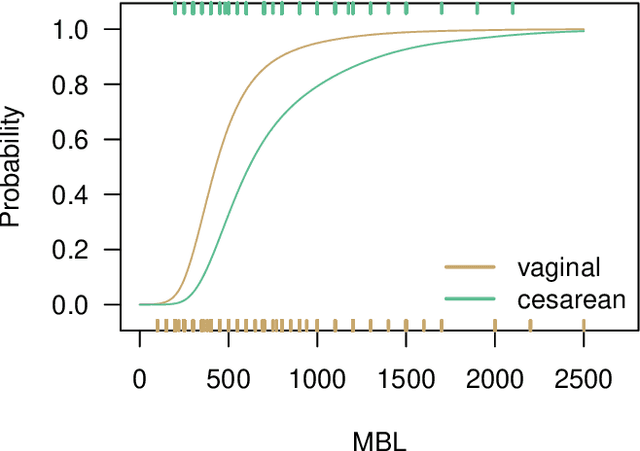
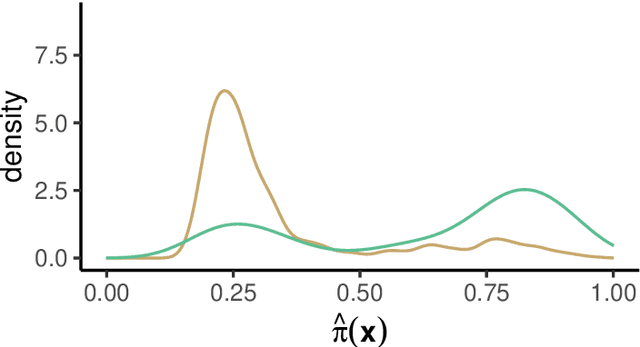
Estimation of heterogeneous treatment effects (HTE) is of prime importance in many disciplines, ranging from personalized medicine to economics among many others. Random forests have been shown to be a flexible and powerful approach to HTE estimation in both randomized trials and observational studies. In particular "causal forests", introduced by Athey, Tibshirani and Wager (2019), along with the R implementation in package grf were rapidly adopted. A related approach, called "model-based forests", that is geared towards randomized trials and simultaneously captures effects of both prognostic and predictive variables, was introduced by Seibold, Zeileis and Hothorn (2018) along with a modular implementation in the R package model4you. Here, we present a unifying view that goes beyond the theoretical motivations and investigates which computational elements make causal forests so successful and how these can be blended with the strengths of model-based forests. To do so, we show that both methods can be understood in terms of the same parameters and model assumptions for an additive model under L2 loss. This theoretical insight allows us to implement several flavors of "model-based causal forests" and dissect their different elements in silico. The original causal forests and model-based forests are compared with the new blended versions in a benchmark study exploring both randomized trials and observational settings. In the randomized setting, both approaches performed akin. If confounding was present in the data generating process, we found local centering of the treatment indicator with the corresponding propensities to be the main driver for good performance. Local centering of the outcome was less important, and might be replaced or enhanced by simultaneous split selection with respect to both prognostic and predictive effects.