Pre-validation Revisited

Pre-validation is a way to build prediction model with two datasets of significantly different feature dimensions. Previous work showed that the asymptotic distribution of test statistic for the pre-validated predictor deviated from a standard Normal, hence will lead to issues in hypothesis tests. In this paper, we revisited the pre-validation procedure and extended the problem formulation without any independence assumption on the two feature sets. We proposed not only an analytical distribution of the test statistics for pre-validated predictor under certain models, but also a generic bootstrap procedure to conduct inference. We showed properties and benefits of pre-validation in prediction, inference and error estimation by simulation and various applications, including analysis of a breast cancer study and a synthetic GWAS example.

Non-identifiability distinguishes Neural Networks among Parametric Models

One of the enduring problems surrounding neural networks is to identify the factors that differentiate them from traditional statistical models. We prove a pair of results which distinguish feedforward neural networks among parametric models at the population level, for regression tasks. Firstly, we prove that for any pair of random variables $(X,Y)$, neural networks always learn a nontrivial relationship between $X$ and $Y$, if one exists. Secondly, we prove that for reasonable smooth parametric models, under local and global identifiability conditions, there exists a nontrivial $(X,Y)$ pair for which the parametric model learns the constant predictor $\mathbb{E}[Y]$. Together, our results suggest that a lack of identifiability distinguishes neural networks among the class of smooth parametric models.

A survey of some recent developments in measures of association

This paper surveys some recent developments in measures of association related to a new coefficient of correlation introduced by the author. A straightforward extension of this coefficient to standard Borel spaces (which includes all Polish spaces), overlooked in the literature so far, is proposed at the end of the survey.

Estimating large causal polytree skeletons from small samples

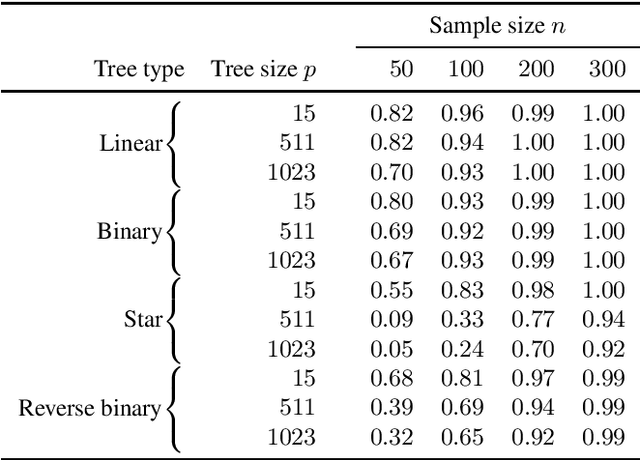
We consider the problem of estimating the skeleton of a large causal polytree from a relatively small i.i.d. sample. This is motivated by the problem of determining causal structure when the number of variables is very large compared to the sample size, such as in gene regulatory networks. We give an algorithm that recovers the tree with high accuracy in such settings. The algorithm works under essentially no distributional or modeling assumptions other than some mild non-degeneracy conditions.

MOSPAT: AutoML based Model Selection and Parameter Tuning for Time Series Anomaly Detection

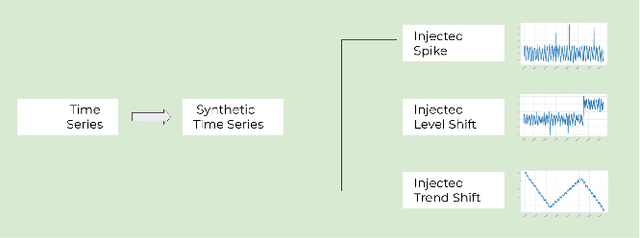
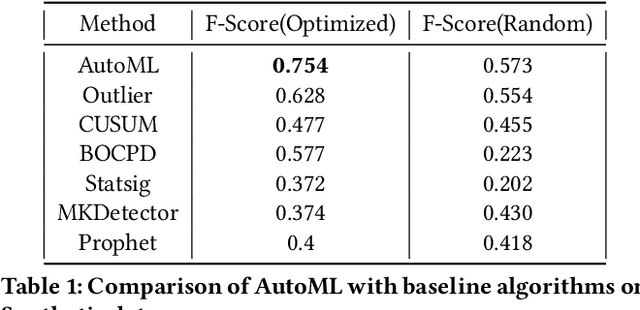
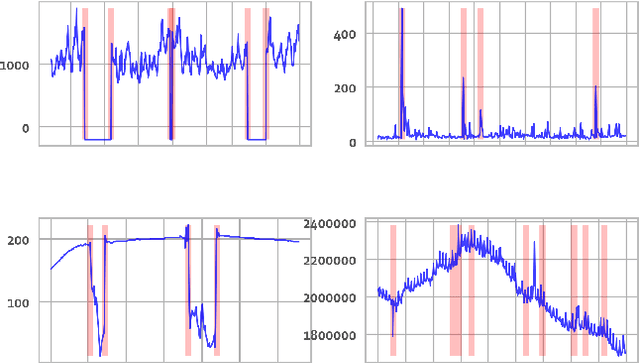
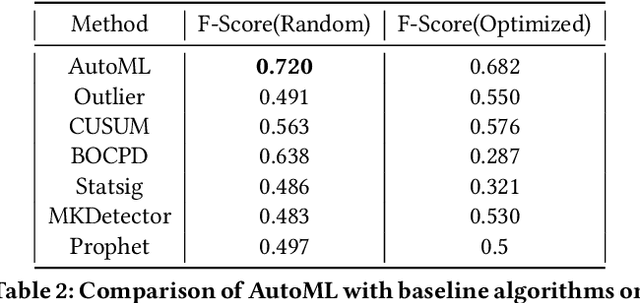
Organizations leverage anomaly and changepoint detection algorithms to detect changes in user behavior or service availability and performance. Many off-the-shelf detection algorithms, though effective, cannot readily be used in large organizations where thousands of users monitor millions of use cases and metrics with varied time series characteristics and anomaly patterns. The selection of algorithm and parameters needs to be precise for each use case: manual tuning does not scale, and automated tuning requires ground truth, which is rarely available. In this paper, we explore MOSPAT, an end-to-end automated machine learning based approach for model and parameter selection, combined with a generative model to produce labeled data. Our scalable end-to-end system allows individual users in large organizations to tailor time-series monitoring to their specific use case and data characteristics, without expert knowledge of anomaly detection algorithms or laborious manual labeling. Our extensive experiments on real and synthetic data demonstrate that this method consistently outperforms using any single algorithm.

Convergence of gradient descent for deep neural networks

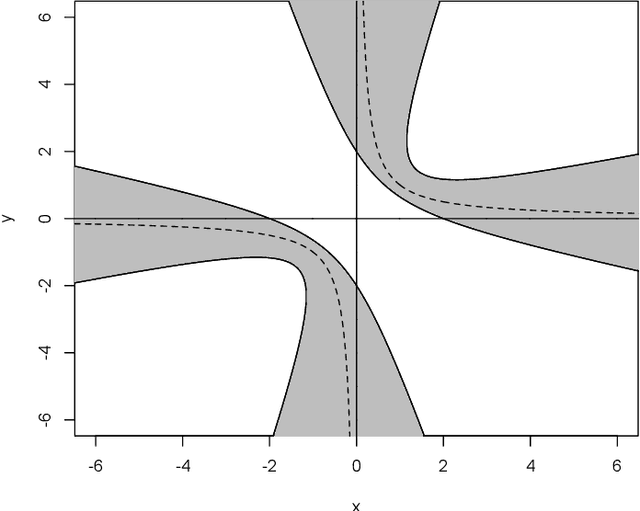
Optimization by gradient descent has been one of main drivers of the "deep learning revolution". Yet, despite some recent progress for extremely wide networks, it remains an open problem to understand why gradient descent often converges to global minima when training deep neural networks. This article presents a new criterion for convergence of gradient descent to a global minimum, which is provably more powerful than the best available criteria from the literature, namely, the Lojasiewicz inequality and its generalizations. This criterion is used to show that gradient descent with proper initialization converges to a global minimum when training any feedforward neural network with smooth and strictly increasing activation functions, provided that the input dimension is greater than or equal to the number of data points.

Micro-Estimates of Wealth for all Low- and Middle-Income Countries

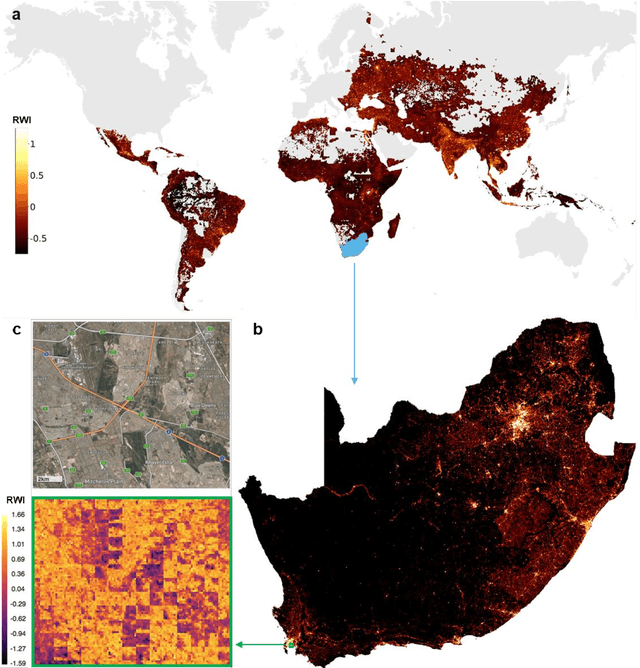
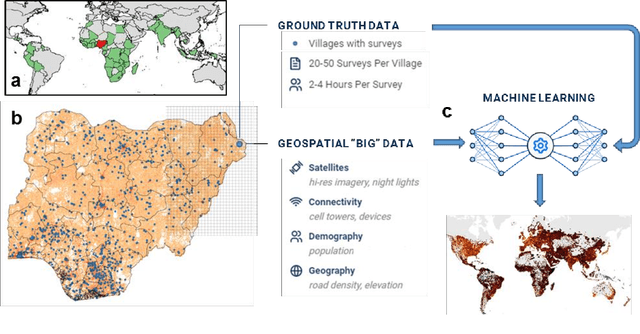
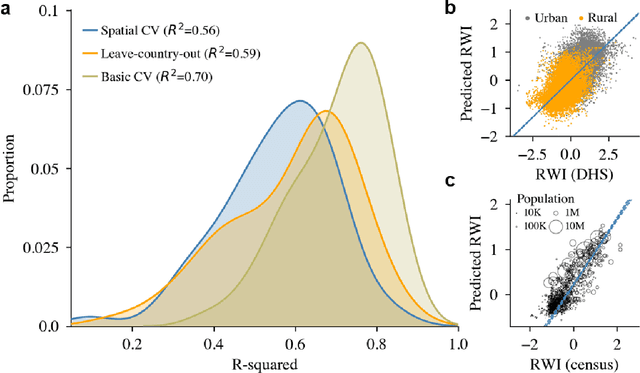
Many critical policy decisions, from strategic investments to the allocation of humanitarian aid, rely on data about the geographic distribution of wealth and poverty. Yet many poverty maps are out of date or exist only at very coarse levels of granularity. Here we develop the first micro-estimates of wealth and poverty that cover the populated surface of all 135 low and middle-income countries (LMICs) at 2.4km resolution. The estimates are built by applying machine learning algorithms to vast and heterogeneous data from satellites, mobile phone networks, topographic maps, as well as aggregated and de-identified connectivity data from Facebook. We train and calibrate the estimates using nationally-representative household survey data from 56 LMICs, then validate their accuracy using four independent sources of household survey data from 18 countries. We also provide confidence intervals for each micro-estimate to facilitate responsible downstream use. These estimates are provided free for public use in the hope that they enable targeted policy response to the COVID-19 pandemic, provide the foundation for new insights into the causes and consequences of economic development and growth, and promote responsible policymaking in support of the Sustainable Development Goals.

Spectral clustering and the high-dimensional stochastic blockmodel

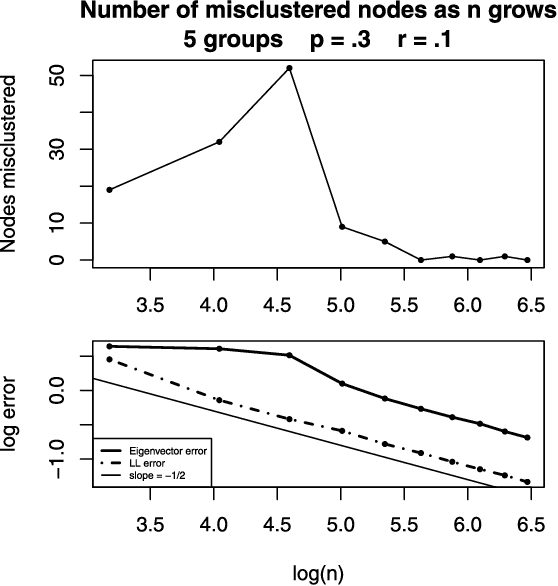
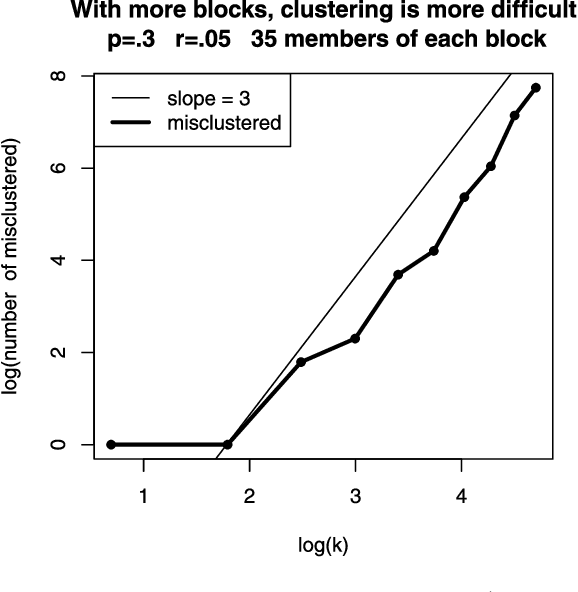
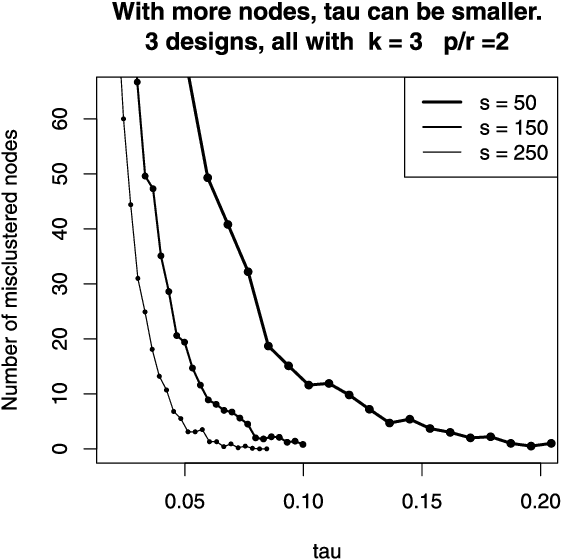
Networks or graphs can easily represent a diverse set of data sources that are characterized by interacting units or actors. Social networks, representing people who communicate with each other, are one example. Communities or clusters of highly connected actors form an essential feature in the structure of several empirical networks. Spectral clustering is a popular and computationally feasible method to discover these communities. The stochastic blockmodel [Social Networks 5 (1983) 109--137] is a social network model with well-defined communities; each node is a member of one community. For a network generated from the Stochastic Blockmodel, we bound the number of nodes "misclustered" by spectral clustering. The asymptotic results in this paper are the first clustering results that allow the number of clusters in the model to grow with the number of nodes, hence the name high-dimensional. In order to study spectral clustering under the stochastic blockmodel, we first show that under the more general latent space model, the eigenvectors of the normalized graph Laplacian asymptotically converge to the eigenvectors of a "population" normalized graph Laplacian. Aside from the implication for spectral clustering, this provides insight into a graph visualization technique. Our method of studying the eigenvectors of random matrices is original.