Corruption-Robust Algorithms with Uncertainty Weighting for Nonlinear Contextual Bandits and Markov Decision Processes

Despite the significant interest and progress in reinforcement learning (RL) problems with adversarial corruption, current works are either confined to the linear setting or lead to an undesired $\tilde{O}(\sqrt{T}\zeta)$ regret bound, where $T$ is the number of rounds and $\zeta$ is the total amount of corruption. In this paper, we consider the contextual bandit with general function approximation and propose a computationally efficient algorithm to achieve a regret of $\tilde{O}(\sqrt{T}+\zeta)$. The proposed algorithm relies on the recently developed uncertainty-weighted least-squares regression from linear contextual bandit \citep{he2022nearly} and a new weighted estimator of uncertainty for the general function class. In contrast to the existing analysis that heavily relies on the linear structure, we develop a novel technique to control the sum of weighted uncertainty, thus establishing the final regret bounds. We then generalize our algorithm to the episodic MDP setting and first achieve an additive dependence on the corruption level $\zeta$ in the scenario of general function approximation. Notably, our algorithms achieve regret bounds either nearly match the performance lower bound or improve the existing methods for all the corruption levels and in both known and unknown $\zeta$ cases.

Nearly Minimax Optimal Reinforcement Learning for Linear Markov Decision Processes

We study reinforcement learning (RL) with linear function approximation. For episodic time-inhomogeneous linear Markov decision processes (linear MDPs) whose transition dynamic can be parameterized as a linear function of a given feature mapping, we propose the first computationally efficient algorithm that achieves the nearly minimax optimal regret $\tilde O(d\sqrt{H^3K})$, where $d$ is the dimension of the feature mapping, $H$ is the planning horizon, and $K$ is the number of episodes. Our algorithm is based on a weighted linear regression scheme with a carefully designed weight, which depends on a new variance estimator that (1) directly estimates the variance of the \emph{optimal} value function, (2) monotonically decreases with respect to the number of episodes to ensure a better estimation accuracy, and (3) uses a rare-switching policy to update the value function estimator to control the complexity of the estimated value function class. Our work provides a complete answer to optimal RL with linear MDPs, and the developed algorithm and theoretical tools may be of independent interest.

A General Framework for Sample-Efficient Function Approximation in Reinforcement Learning

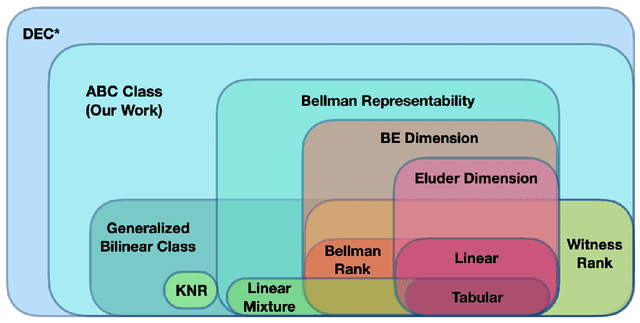
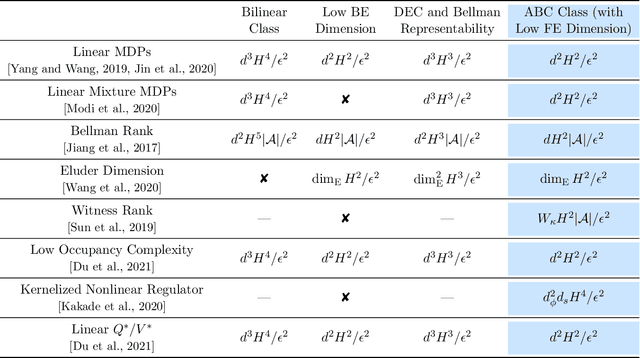
With the increasing need for handling large state and action spaces, general function approximation has become a key technique in reinforcement learning (RL). In this paper, we propose a general framework that unifies model-based and model-free RL, and an Admissible Bellman Characterization (ABC) class that subsumes nearly all Markov Decision Process (MDP) models in the literature for tractable RL. We propose a novel estimation function with decomposable structural properties for optimization-based exploration and the functional eluder dimension as a complexity measure of the ABC class. Under our framework, a new sample-efficient algorithm namely OPtimization-based ExploRation with Approximation (OPERA) is proposed, achieving regret bounds that match or improve over the best-known results for a variety of MDP models. In particular, for MDPs with low Witness rank, under a slightly stronger assumption, OPERA improves the state-of-the-art sample complexity results by a factor of $dH$. Our framework provides a generic interface to design and analyze new RL models and algorithms.

Learning Two-Player Mixture Markov Games: Kernel Function Approximation and Correlated Equilibrium

We consider learning Nash equilibria in two-player zero-sum Markov Games with nonlinear function approximation, where the action-value function is approximated by a function in a Reproducing Kernel Hilbert Space (RKHS). The key challenge is how to do exploration in the high-dimensional function space. We propose a novel online learning algorithm to find a Nash equilibrium by minimizing the duality gap. At the core of our algorithms are upper and lower confidence bounds that are derived based on the principle of optimism in the face of uncertainty. We prove that our algorithm is able to attain an $O(\sqrt{T})$ regret with polynomial computational complexity, under very mild assumptions on the reward function and the underlying dynamic of the Markov Games. We also propose several extensions of our algorithm, including an algorithm with Bernstein-type bonus that can achieve a tighter regret bound, and another algorithm for model misspecification that can be applied to neural function approximation.

Towards Understanding Mixture of Experts in Deep Learning

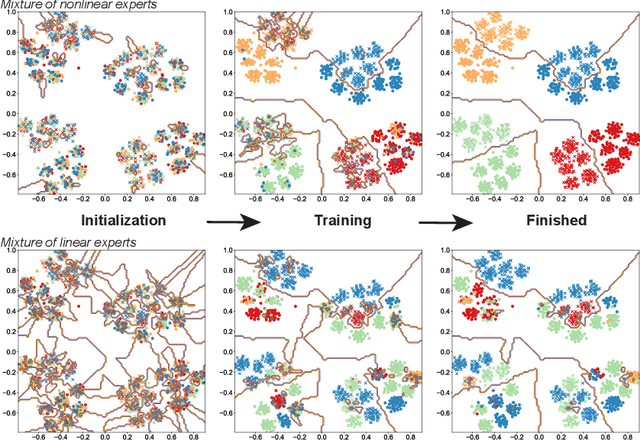
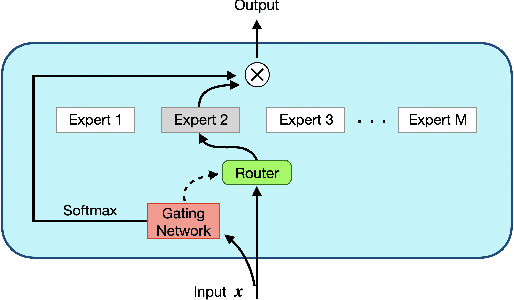
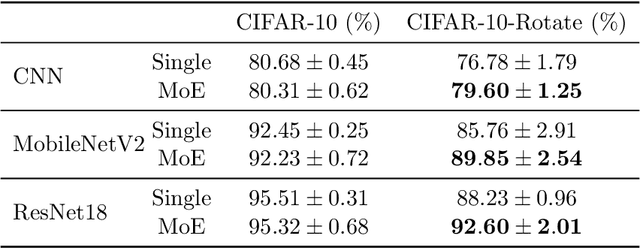
The Mixture-of-Experts (MoE) layer, a sparsely-activated model controlled by a router, has achieved great success in deep learning. However, the understanding of such architecture remains elusive. In this paper, we formally study how the MoE layer improves the performance of neural network learning and why the mixture model will not collapse into a single model. Our empirical results suggest that the cluster structure of the underlying problem and the non-linearity of the expert are pivotal to the success of MoE. To further understand this, we consider a challenging classification problem with intrinsic cluster structures, which is hard to learn using a single expert. Yet with the MoE layer, by choosing the experts as two-layer nonlinear convolutional neural networks (CNNs), we show that the problem can be learned successfully. Furthermore, our theory shows that the router can learn the cluster-center features, which helps divide the input complex problem into simpler linear classification sub-problems that individual experts can conquer. To our knowledge, this is the first result towards formally understanding the mechanism of the MoE layer for deep learning.

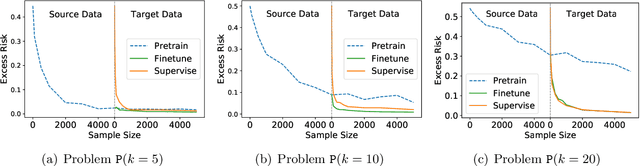
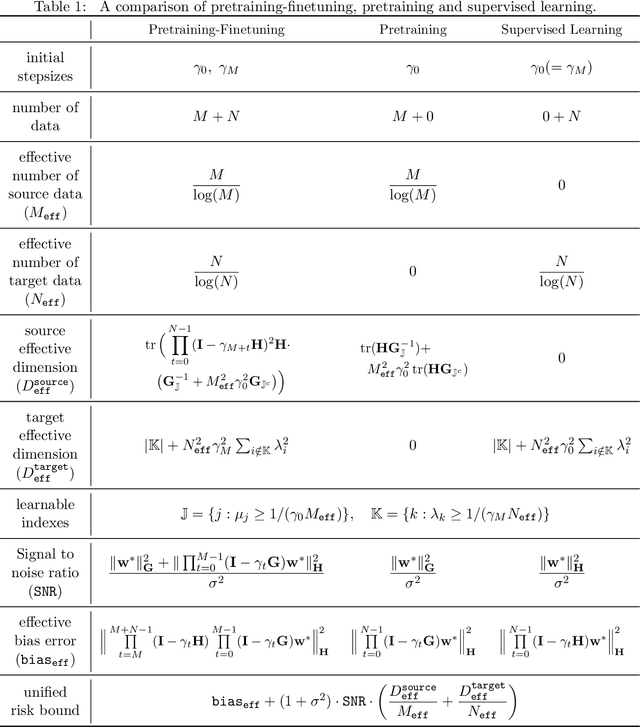
The Power and Limitation of Pretraining-Finetuning for Linear Regression under Covariate Shift

We study linear regression under covariate shift, where the marginal distribution over the input covariates differs in the source and the target domains, while the conditional distribution of the output given the input covariates is similar across the two domains. We investigate a transfer learning approach with pretraining on the source data and finetuning based on the target data (both conducted by online SGD) for this problem. We establish sharp instance-dependent excess risk upper and lower bounds for this approach. Our bounds suggest that for a large class of linear regression instances, transfer learning with $O(N^2)$ source data (and scarce or no target data) is as effective as supervised learning with $N$ target data. In addition, we show that finetuning, even with only a small amount of target data, could drastically reduce the amount of source data required by pretraining. Our theory sheds light on the effectiveness and limitation of pretraining as well as the benefits of finetuning for tackling covariate shift problems.

A Simple and Provably Efficient Algorithm for Asynchronous Federated Contextual Linear Bandits

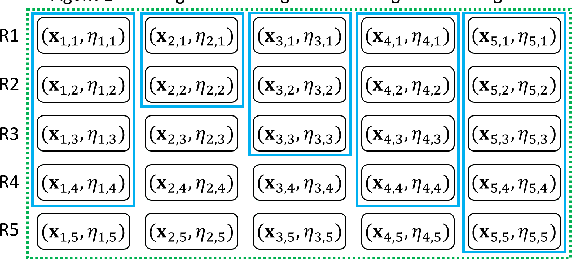
We study federated contextual linear bandits, where $M$ agents cooperate with each other to solve a global contextual linear bandit problem with the help of a central server. We consider the asynchronous setting, where all agents work independently and the communication between one agent and the server will not trigger other agents' communication. We propose a simple algorithm named \texttt{FedLinUCB} based on the principle of optimism. We prove that the regret of \texttt{FedLinUCB} is bounded by $\tilde{O}(d\sqrt{\sum_{m=1}^M T_m})$ and the communication complexity is $\tilde{O}(dM^2)$, where $d$ is the dimension of the contextual vector and $T_m$ is the total number of interactions with the environment by $m$-th agent. To the best of our knowledge, this is the first provably efficient algorithm that allows fully asynchronous communication for federated contextual linear bandits, while achieving the same regret guarantee as in the single-agent setting.

Computationally Efficient Horizon-Free Reinforcement Learning for Linear Mixture MDPs

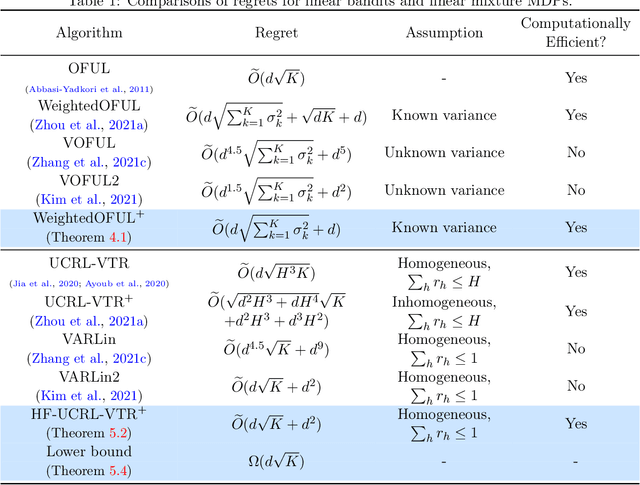
Recent studies have shown that episodic reinforcement learning (RL) is not more difficult than contextual bandits, even with a long planning horizon and unknown state transitions. However, these results are limited to either tabular Markov decision processes (MDPs) or computationally inefficient algorithms for linear mixture MDPs. In this paper, we propose the first computationally efficient horizon-free algorithm for linear mixture MDPs, which achieves the optimal $\tilde O(d\sqrt{K} +d^2)$ regret up to logarithmic factors. Our algorithm adapts a weighted least square estimator for the unknown transitional dynamic, where the weight is both \emph{variance-aware} and \emph{uncertainty-aware}. When applying our weighted least square estimator to heterogeneous linear bandits, we can obtain an $\tilde O(d\sqrt{\sum_{k=1}^K \sigma_k^2} +d)$ regret in the first $K$ rounds, where $d$ is the dimension of the context and $\sigma_k^2$ is the variance of the reward in the $k$-th round. This also improves upon the best-known algorithms in this setting when $\sigma_k^2$'s are known.

Nearly Optimal Algorithms for Linear Contextual Bandits with Adversarial Corruptions

We study the linear contextual bandit problem in the presence of adversarial corruption, where the reward at each round is corrupted by an adversary, and the corruption level (i.e., the sum of corruption magnitudes over the horizon) is $C\geq 0$. The best-known algorithms in this setting are limited in that they either are computationally inefficient or require a strong assumption on the corruption, or their regret is at least $C$ times worse than the regret without corruption. In this paper, to overcome these limitations, we propose a new algorithm based on the principle of optimism in the face of uncertainty. At the core of our algorithm is a weighted ridge regression where the weight of each chosen action depends on its confidence up to some threshold. We show that for both known $C$ and unknown $C$ cases, our algorithm with proper choice of hyperparameter achieves a regret that nearly matches the lower bounds. Thus, our algorithm is nearly optimal up to logarithmic factors for both cases. Notably, our algorithm achieves the near-optimal regret for both corrupted and uncorrupted cases ($C=0$) simultaneously.

On the Convergence of Certified Robust Training with Interval Bound Propagation

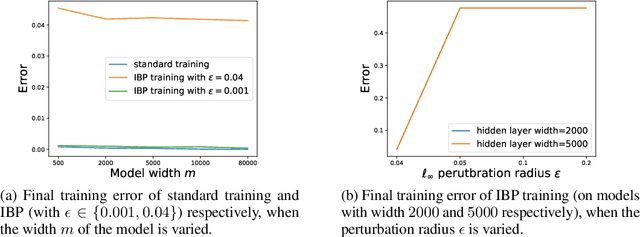
Interval Bound Propagation (IBP) is so far the base of state-of-the-art methods for training neural networks with certifiable robustness guarantees when potential adversarial perturbations present, while the convergence of IBP training remains unknown in existing literature. In this paper, we present a theoretical analysis on the convergence of IBP training. With an overparameterized assumption, we analyze the convergence of IBP robust training. We show that when using IBP training to train a randomly initialized two-layer ReLU neural network with logistic loss, gradient descent can linearly converge to zero robust training error with a high probability if we have sufficiently small perturbation radius and large network width.