GraphGLOW: Universal and Generalizable Structure Learning for Graph Neural Networks

Graph structure learning is a well-established problem that aims at optimizing graph structures adaptive to specific graph datasets to help message passing neural networks (i.e., GNNs) to yield effective and robust node embeddings. However, the common limitation of existing models lies in the underlying \textit{closed-world assumption}: the testing graph is the same as the training graph. This premise requires independently training the structure learning model from scratch for each graph dataset, which leads to prohibitive computation costs and potential risks for serious over-fitting. To mitigate these issues, this paper explores a new direction that moves forward to learn a universal structure learning model that can generalize across graph datasets in an open world. We first introduce the mathematical definition of this novel problem setting, and describe the model formulation from a probabilistic data-generative aspect. Then we devise a general framework that coordinates a single graph-shared structure learner and multiple graph-specific GNNs to capture the generalizable patterns of optimal message-passing topology across datasets. The well-trained structure learner can directly produce adaptive structures for unseen target graphs without any fine-tuning. Across diverse datasets and various challenging cross-graph generalization protocols, our experiments show that even without training on target graphs, the proposed model i) significantly outperforms expressive GNNs trained on input (non-optimized) topology, and ii) surprisingly performs on par with state-of-the-art models that independently optimize adaptive structures for specific target graphs, with notably orders-of-magnitude acceleration for training on the target graph.

Simplifying and Empowering Transformers for Large-Graph Representations

Learning representations on large-sized graphs is a long-standing challenge due to the inter-dependence nature involved in massive data points. Transformers, as an emerging class of foundation encoders for graph-structured data, have shown promising performance on small graphs due to its global attention capable of capturing all-pair influence beyond neighboring nodes. Even so, existing approaches tend to inherit the spirit of Transformers in language and vision tasks, and embrace complicated models by stacking deep multi-head attentions. In this paper, we critically demonstrate that even using a one-layer attention can bring up surprisingly competitive performance across node property prediction benchmarks where node numbers range from thousand-level to billion-level. This encourages us to rethink the design philosophy for Transformers on large graphs, where the global attention is a computation overhead hindering the scalability. We frame the proposed scheme as Simplified Graph Transformers (SGFormer), which is empowered by a simple attention model that can efficiently propagate information among arbitrary nodes in one layer. SGFormer requires none of positional encodings, feature/graph pre-processing or augmented loss. Empirically, SGFormer successfully scales to the web-scale graph ogbn-papers100M and yields up to 141x inference acceleration over SOTA Transformers on medium-sized graphs. Beyond current results, we believe the proposed methodology alone enlightens a new technical path of independent interest for building Transformers on large graphs.

NodeFormer: A Scalable Graph Structure Learning Transformer for Node Classification

Graph neural networks have been extensively studied for learning with inter-connected data. Despite this, recent evidence has revealed GNNs' deficiencies related to over-squashing, heterophily, handling long-range dependencies, edge incompleteness and particularly, the absence of graphs altogether. While a plausible solution is to learn new adaptive topology for message passing, issues concerning quadratic complexity hinder simultaneous guarantees for scalability and precision in large networks. In this paper, we introduce a novel all-pair message passing scheme for efficiently propagating node signals between arbitrary nodes, as an important building block for a pioneering Transformer-style network for node classification on large graphs, dubbed as \textsc{NodeFormer}. Specifically, the efficient computation is enabled by a kernerlized Gumbel-Softmax operator that reduces the algorithmic complexity to linearity w.r.t. node numbers for learning latent graph structures from large, potentially fully-connected graphs in a differentiable manner. We also provide accompanying theory as justification for our design. Extensive experiments demonstrate the promising efficacy of the method in various tasks including node classification on graphs (with up to 2M nodes) and graph-enhanced applications (e.g., image classification) where input graphs are missing.

Energy-based Out-of-Distribution Detection for Graph Neural Networks

Learning on graphs, where instance nodes are inter-connected, has become one of the central problems for deep learning, as relational structures are pervasive and induce data inter-dependence which hinders trivial adaptation of existing approaches that assume inputs to be i.i.d.~sampled. However, current models mostly focus on improving testing performance of in-distribution data and largely ignore the potential risk w.r.t. out-of-distribution (OOD) testing samples that may cause negative outcome if the prediction is overconfident on them. In this paper, we investigate the under-explored problem, OOD detection on graph-structured data, and identify a provably effective OOD discriminator based on an energy function directly extracted from graph neural networks trained with standard classification loss. This paves a way for a simple, powerful and efficient OOD detection model for GNN-based learning on graphs, which we call GNNSafe. It also has nice theoretical properties that guarantee an overall distinguishable margin between the detection scores for in-distribution and OOD samples, which, more critically, can be further strengthened by a learning-free energy belief propagation scheme. For comprehensive evaluation, we introduce new benchmark settings that evaluate the model for detecting OOD data from both synthetic and real distribution shifts (cross-domain graph shifts and temporal graph shifts). The results show that GNNSafe achieves up to $17.0\%$ AUROC improvement over state-of-the-arts and it could serve as simple yet strong baselines in such an under-developed area.

DIFFormer: Scalable (Graph) Transformers Induced by Energy Constrained Diffusion

Real-world data generation often involves complex inter-dependencies among instances, violating the IID-data hypothesis of standard learning paradigms and posing a challenge for uncovering the geometric structures for learning desired instance representations. To this end, we introduce an energy constrained diffusion model which encodes a batch of instances from a dataset into evolutionary states that progressively incorporate other instances' information by their interactions. The diffusion process is constrained by descent criteria w.r.t.~a principled energy function that characterizes the global consistency of instance representations over latent structures. We provide rigorous theory that implies closed-form optimal estimates for the pairwise diffusion strength among arbitrary instance pairs, which gives rise to a new class of neural encoders, dubbed as DIFFormer (diffusion-based Transformers), with two instantiations: a simple version with linear complexity for prohibitive instance numbers, and an advanced version for learning complex structures. Experiments highlight the wide applicability of our model as a general-purpose encoder backbone with superior performance in various tasks, such as node classification on large graphs, semi-supervised image/text classification, and spatial-temporal dynamics prediction.

Graph Neural Networks are Inherently Good Generalizers: Insights by Bridging GNNs and MLPs

Graph neural networks (GNNs), as the de-facto model class for representation learning on graphs, are built upon the multi-layer perceptrons (MLP) architecture with additional message passing layers to allow features to flow across nodes. While conventional wisdom largely attributes the success of GNNs to their advanced expressivity for learning desired functions on nodes' ego-graphs, we conjecture that this is \emph{not} the main cause of GNNs' superiority in node prediction tasks. This paper pinpoints the major source of GNNs' performance gain to their intrinsic generalization capabilities, by introducing an intermediate model class dubbed as P(ropagational)MLP, which is identical to standard MLP in training, and then adopt GNN's architecture in testing. Intriguingly, we observe that PMLPs consistently perform on par with (or even exceed) their GNN counterparts across ten benchmarks and different experimental settings, despite the fact that PMLPs share the same (trained) weights with poorly-performed MLP. This critical finding opens a door to a brand new perspective for understanding the power of GNNs, and allow bridging GNNs and MLPs for dissecting their generalization behaviors. As an initial step to analyze PMLP, we show its essential difference with MLP at infinite-width limit lies in the NTK feature map in the post-training stage. Moreover, though MLP and PMLP cannot extrapolate non-linear functions for extreme OOD data, PMLP has more freedom to generalize near the training support.

Localized Contrastive Learning on Graphs

Contrastive learning methods based on InfoNCE loss are popular in node representation learning tasks on graph-structured data. However, its reliance on data augmentation and its quadratic computational complexity might lead to inconsistency and inefficiency problems. To mitigate these limitations, in this paper, we introduce a simple yet effective contrastive model named Localized Graph Contrastive Learning (Local-GCL in short). Local-GCL consists of two key designs: 1) We fabricate the positive examples for each node directly using its first-order neighbors, which frees our method from the reliance on carefully-designed graph augmentations; 2) To improve the efficiency of contrastive learning on graphs, we devise a kernelized contrastive loss, which could be approximately computed in linear time and space complexity with respect to the graph size. We provide theoretical analysis to justify the effectiveness and rationality of the proposed methods. Experiments on various datasets with different scales and properties demonstrate that in spite of its simplicity, Local-GCL achieves quite competitive performance in self-supervised node representation learning tasks on graphs with various scales and properties.

Geometric Knowledge Distillation: Topology Compression for Graph Neural Networks

We study a new paradigm of knowledge transfer that aims at encoding graph topological information into graph neural networks (GNNs) by distilling knowledge from a teacher GNN model trained on a complete graph to a student GNN model operating on a smaller or sparser graph. To this end, we revisit the connection between thermodynamics and the behavior of GNN, based on which we propose Neural Heat Kernel (NHK) to encapsulate the geometric property of the underlying manifold concerning the architecture of GNNs. A fundamental and principled solution is derived by aligning NHKs on teacher and student models, dubbed as Geometric Knowledge Distillation. We develop non- and parametric instantiations and demonstrate their efficacy in various experimental settings for knowledge distillation regarding different types of privileged topological information and teacher-student schemes.

Towards Out-of-Distribution Sequential Event Prediction: A Causal Treatment

The goal of sequential event prediction is to estimate the next event based on a sequence of historical events, with applications to sequential recommendation, user behavior analysis and clinical treatment. In practice, the next-event prediction models are trained with sequential data collected at one time and need to generalize to newly arrived sequences in remote future, which requires models to handle temporal distribution shift from training to testing. In this paper, we first take a data-generating perspective to reveal a negative result that existing approaches with maximum likelihood estimation would fail for distribution shift due to the latent context confounder, i.e., the common cause for the historical events and the next event. Then we devise a new learning objective based on backdoor adjustment and further harness variational inference to make it tractable for sequence learning problems. On top of that, we propose a framework with hierarchical branching structures for learning context-specific representations. Comprehensive experiments on diverse tasks (e.g., sequential recommendation) demonstrate the effectiveness, applicability and scalability of our method with various off-the-shelf models as backbones.

Trading Hard Negatives and True Negatives: A Debiased Contrastive Collaborative Filtering Approach

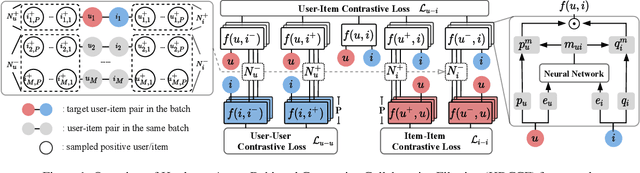
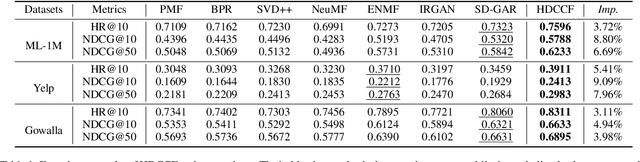
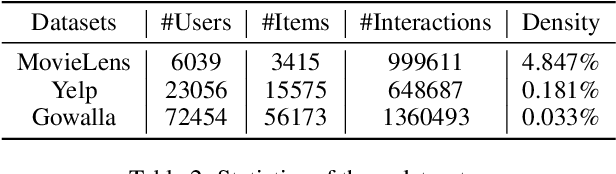
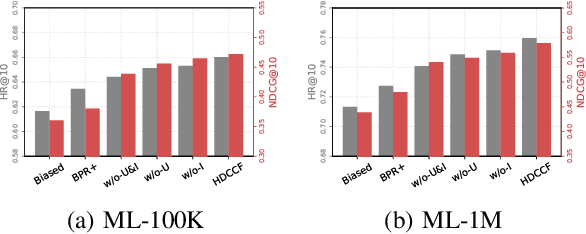
Collaborative filtering (CF), as a standard method for recommendation with implicit feedback, tackles a semi-supervised learning problem where most interaction data are unobserved. Such a nature makes existing approaches highly rely on mining negatives for providing correct training signals. However, mining proper negatives is not a free lunch, encountering with a tricky trade-off between mining informative hard negatives and avoiding false ones. We devise a new approach named as Hardness-Aware Debiased Contrastive Collaborative Filtering (HDCCF) to resolve the dilemma. It could sufficiently explore hard negatives from two-fold aspects: 1) adaptively sharpening the gradients of harder instances through a set-wise objective, and 2) implicitly leveraging item/user frequency information with a new sampling strategy. To circumvent false negatives, we develop a principled approach to improve the reliability of negative instances and prove that the objective is an unbiased estimation of sampling from the true negative distribution. Extensive experiments demonstrate the superiority of the proposed model over existing CF models and hard negative mining methods.