Optimizing Shortfall Risk Metric for Learning Regression Models

We consider the problem of estimating and optimizing utility-based shortfall risk (UBSR) of a loss, say $(Y - \hat Y)^2$, in the context of a regression problem. Empirical risk minimization with a UBSR objective is challenging since UBSR is a non-linear function of the underlying distribution. We first derive a concentration bound for UBSR estimation using independent and identically distributed (i.i.d.) samples. We then frame the UBSR optimization problem as minimization of a pseudo-linear function in the space of achievable distributions $\mathcal D$ of the loss $(Y- \hat Y)^2$. We construct a gradient oracle for the UBSR objective and a linear minimization oracle (LMO) for the set $\mathcal D$. Using these oracles, we devise a bisection-type algorithm, and establish convergence to the UBSR-optimal solution.

Impact of Label Noise on Learning Complex Features

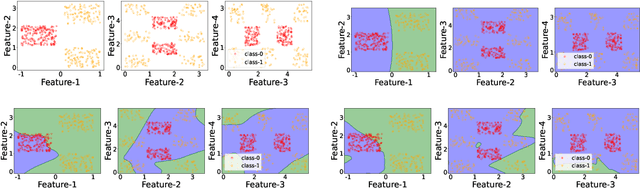
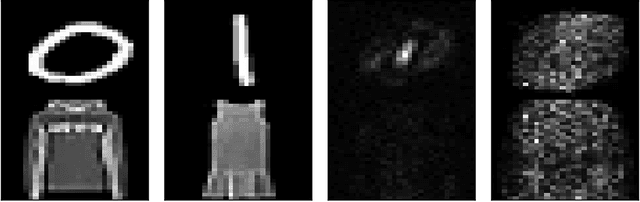
Neural networks trained with stochastic gradient descent exhibit an inductive bias towards simpler decision boundaries, typically converging to a narrow family of functions, and often fail to capture more complex features. This phenomenon raises concerns about the capacity of deep models to adequately learn and represent real-world datasets. Traditional approaches such as explicit regularization, data augmentation, architectural modifications, etc., have largely proven ineffective in encouraging the models to learn diverse features. In this work, we investigate the impact of pre-training models with noisy labels on the dynamics of SGD across various architectures and datasets. We show that pretraining promotes learning complex functions and diverse features in the presence of noise. Our experiments demonstrate that pre-training with noisy labels encourages gradient descent to find alternate minima that do not solely depend upon simple features, rather learns more complex and broader set of features, without hurting performance.

Graph Classification with GNNs: Optimisation, Representation and Inductive Bias

Theoretical studies on the representation power of GNNs have been centered around understanding the equivalence of GNNs, using WL-Tests for detecting graph isomorphism. In this paper, we argue that such equivalence ignores the accompanying optimization issues and does not provide a holistic view of the GNN learning process. We illustrate these gaps between representation and optimization with examples and experiments. We also explore the existence of an implicit inductive bias (e.g. fully connected networks prefer to learn low frequency functions in their input space) in GNNs, in the context of graph classification tasks. We further prove theoretically that the message-passing layers in the graph, have a tendency to search for either discriminative subgraphs, or a collection of discriminative nodes dispersed across the graph, depending on the different global pooling layers used. We empirically verify this bias through experiments over real-world and synthetic datasets. Finally, we show how our work can help in incorporating domain knowledge via attention based architectures, and can evince their capability to discriminate coherent subgraphs.

On the Learning Dynamics of Attention Networks

Attention models are typically learned by optimizing one of three standard loss functions that are variously called -- soft attention, hard attention, and latent variable marginal likelihood (LVML) attention. All three paradigms are motivated by the same goal of finding two models -- a `focus' model that `selects' the right \textit{segment} of the input and a `classification' model that processes the selected segment into the target label. However, they differ significantly in the way the selected segments are aggregated, resulting in distinct dynamics and final results. We observe a unique signature of models learned using these paradigms and explain this as a consequence of the evolution of the classification model under gradient descent when the focus model is fixed. We also analyze these paradigms in a simple setting and derive closed-form expressions for the parameter trajectory under gradient flow. With the soft attention loss, the focus model improves quickly at initialization and splutters later on. On the other hand, hard attention loss behaves in the opposite fashion. Based on our observations, we propose a simple hybrid approach that combines the advantages of the different loss functions and demonstrates it on a collection of semi-synthetic and real-world datasets

On the Interpretability of Attention Networks

Attention mechanisms form a core component of several successful deep learning architectures, and are based on one key idea: ''The output depends only on a small (but unknown) segment of the input.'' In several practical applications like image captioning and language translation, this is mostly true. In trained models with an attention mechanism, the outputs of an intermediate module that encodes the segment of input responsible for the output is often used as a way to peek into the `reasoning` of the network. We make such a notion more precise for a variant of the classification problem that we term selective dependence classification (SDC) when used with attention model architectures. Under such a setting, we demonstrate various error modes where an attention model can be accurate but fail to be interpretable, and show that such models do occur as a result of training. We illustrate various situations that can accentuate and mitigate this behaviour. Finally, we use our objective definition of interpretability for SDC tasks to evaluate a few attention model learning algorithms designed to encourage sparsity and demonstrate that these algorithms help improve interpretability.

Consistent Multiclass Algorithms for Complex Metrics and Constraints

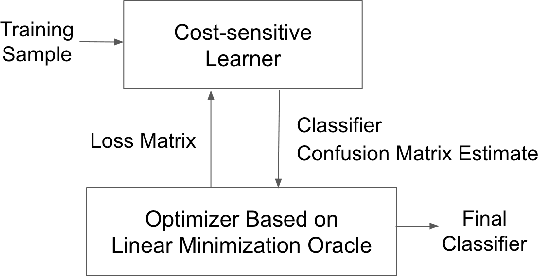
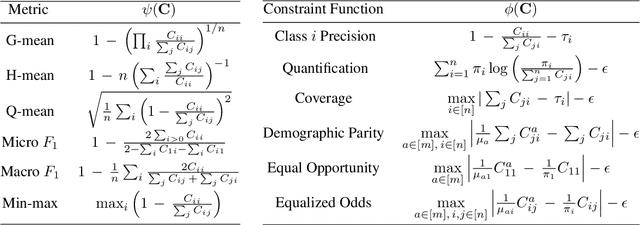
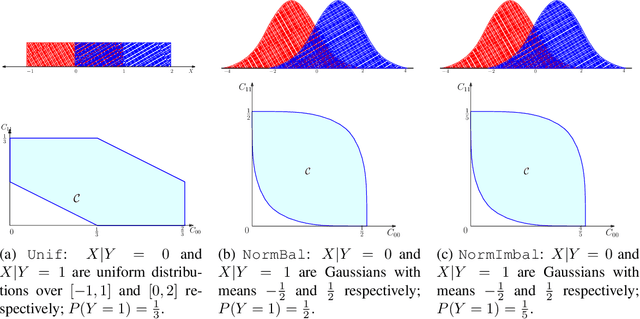
We present consistent algorithms for multiclass learning with complex performance metrics and constraints, where the objective and constraints are defined by arbitrary functions of the confusion matrix. This setting includes many common performance metrics such as the multiclass G-mean and micro F1-measure, and constraints such as those on the classifier's precision and recall and more recent measures of fairness discrepancy. We give a general framework for designing consistent algorithms for such complex design goals by viewing the learning problem as an optimization problem over the set of feasible confusion matrices. We provide multiple instantiations of our framework under different assumptions on the performance metrics and constraints, and in each case show rates of convergence to the optimal (feasible) classifier (and thus asymptotic consistency). Experiments on a variety of multiclass classification tasks and fairness-constrained problems show that our algorithms compare favorably to the state-of-the-art baselines.

Predicting the success of Gradient Descent for a particular Dataset-Architecture-Initialization (DAI)

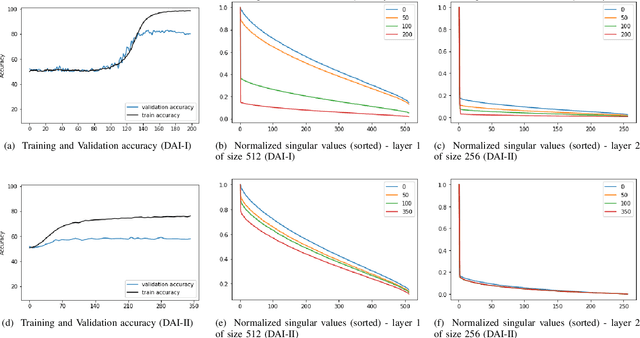
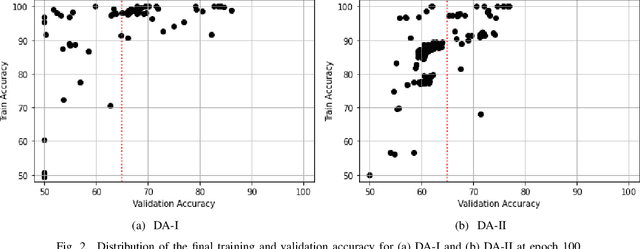
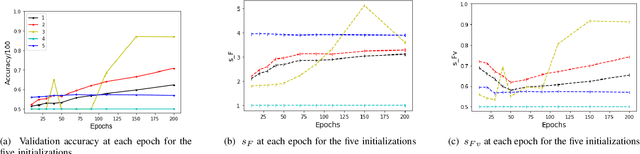
Despite their massive success, training successful deep neural networks still largely relies on experimentally choosing an architecture, hyper-parameters, initialization, and training mechanism. In this work, we focus on determining the success of standard gradient descent method for training deep neural networks on a specified dataset, architecture, and initialization (DAI) combination. Through extensive systematic experiments, we show that the evolution of singular values of the matrix obtained from the hidden layers of a DNN can aid in determining the success of gradient descent technique to train a DAI, even in the absence of validation labels in the supervised learning paradigm. This phenomenon can facilitate early give-up, stopping the training of neural networks which are predicted to not generalize well, early in the training process. Our experimentation across multiple datasets, architectures, and initializations reveals that the proposed scores can more accurately predict the success of a DAI than simply relying on the validation accuracy at earlier epochs to make a judgment.

Using noise resilience for ranking generalization of deep neural networks

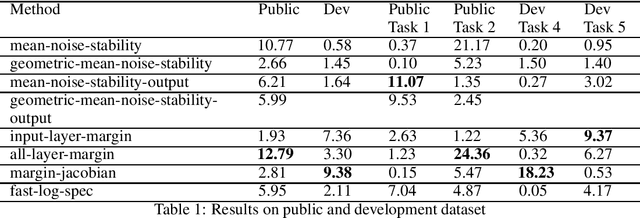
Recent papers have shown that sufficiently overparameterized neural networks can perfectly fit even random labels. Thus, it is crucial to understand the underlying reason behind the generalization performance of a network on real-world data. In this work, we propose several measures to predict the generalization error of a network given the training data and its parameters. Using one of these measures, based on noise resilience of the network, we secured 5th position in the predicting generalization in deep learning (PGDL) competition at NeurIPS 2020.

Inductive Bias of Gradient Descent for Exponentially Weight Normalized Smooth Homogeneous Neural Nets

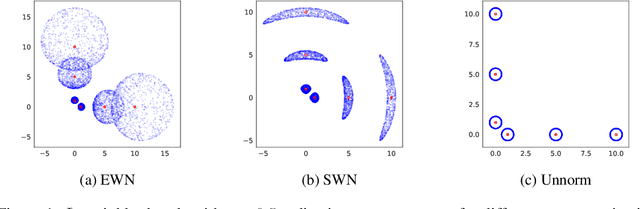
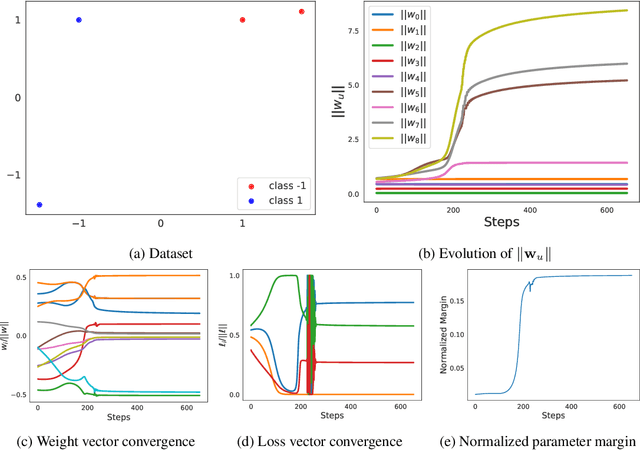
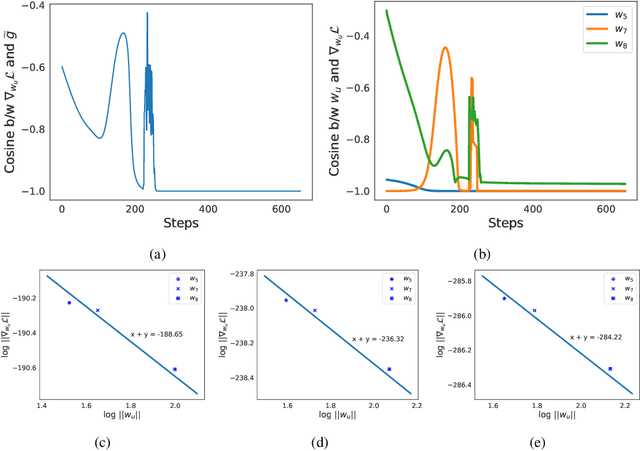
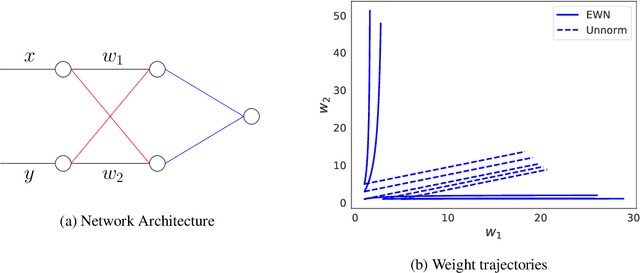
We analyze the inductive bias of gradient descent for weight normalized smooth homogeneous neural nets, when trained on exponential or cross-entropy loss. Our analysis focuses on exponential weight normalization (EWN), which encourages weight updates along the radial direction. This paper shows that the gradient flow path with EWN is equivalent to gradient flow on standard networks with an adaptive learning rate, and hence causes the weights to be updated in a way that prefers asymptotic relative sparsity. These results can be extended to hold for gradient descent via an appropriate adaptive learning rate. The asymptotic convergence rate of the loss in this setting is given by $\Theta(\frac{1}{t(\log t)^2})$, and is independent of the depth of the network. We contrast these results with the inductive bias of standard weight normalization (SWN) and unnormalized architectures, and demonstrate their implications on synthetic data sets.Experimental results on simple data sets and architectures support our claim on sparse EWN solutions, even with SGD. This demonstrates its potential applications in learning prunable neural networks.

Convex Calibrated Surrogates for the Multi-Label F-Measure

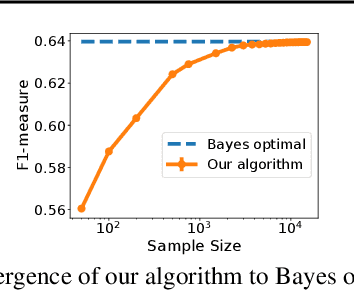
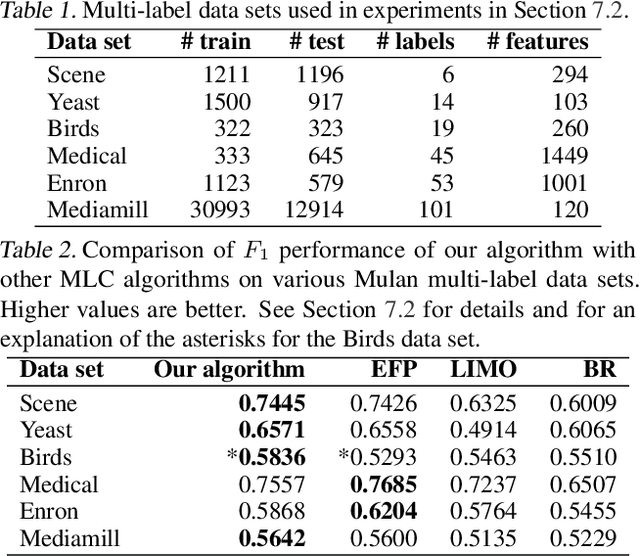
The F-measure is a widely used performance measure for multi-label classification, where multiple labels can be active in an instance simultaneously (e.g. in image tagging, multiple tags can be active in any image). In particular, the F-measure explicitly balances recall (fraction of active labels predicted to be active) and precision (fraction of labels predicted to be active that are actually so), both of which are important in evaluating the overall performance of a multi-label classifier. As with most discrete prediction problems, however, directly optimizing the F-measure is computationally hard. In this paper, we explore the question of designing convex surrogate losses that are calibrated for the F-measure -- specifically, that have the property that minimizing the surrogate loss yields (in the limit of sufficient data) a Bayes optimal multi-label classifier for the F-measure. We show that the F-measure for an $s$-label problem, when viewed as a $2^s \times 2^s$ loss matrix, has rank at most $s^2+1$, and apply a result of Ramaswamy et al. (2014) to design a family of convex calibrated surrogates for the F-measure. The resulting surrogate risk minimization algorithms can be viewed as decomposing the multi-label F-measure learning problem into $s^2+1$ binary class probability estimation problems. We also provide a quantitative regret transfer bound for our surrogates, which allows any regret guarantees for the binary problems to be transferred to regret guarantees for the overall F-measure problem, and discuss a connection with the algorithm of Dembczynski et al. (2013). Our experiments confirm our theoretical findings.