Consistency Conditions for Differentiable Surrogate Losses

The statistical consistency of surrogate losses for discrete prediction tasks is often checked via the condition of calibration. However, directly verifying calibration can be arduous. Recent work shows that for polyhedral surrogates, a less arduous condition, indirect elicitation (IE), is still equivalent to calibration. We give the first results of this type for non-polyhedral surrogates, specifically the class of convex differentiable losses. We first prove that under mild conditions, IE and calibration are equivalent for one-dimensional losses in this class. We construct a counter-example that shows that this equivalence fails in higher dimensions. This motivates the introduction of strong IE, a strengthened form of IE that is equally easy to verify. We establish that strong IE implies calibration for differentiable surrogates and is both necessary and sufficient for strongly convex, differentiable surrogates. Finally, we apply these results to a range of problems to demonstrate the power of IE and strong IE for designing and analyzing consistent differentiable surrogates.

Consistent Multiclass Algorithms for Complex Metrics and Constraints

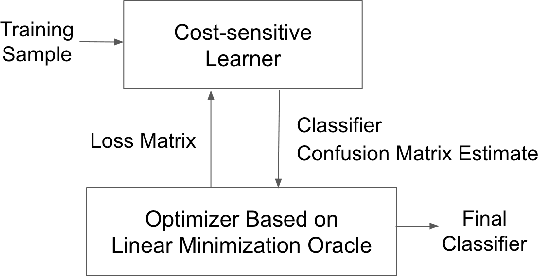
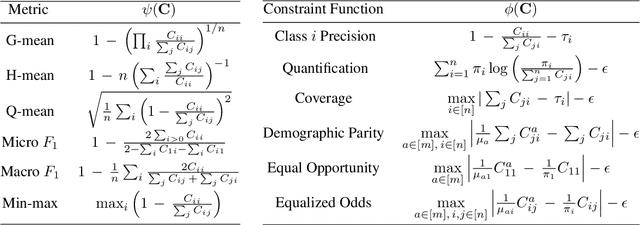
We present consistent algorithms for multiclass learning with complex performance metrics and constraints, where the objective and constraints are defined by arbitrary functions of the confusion matrix. This setting includes many common performance metrics such as the multiclass G-mean and micro F1-measure, and constraints such as those on the classifier's precision and recall and more recent measures of fairness discrepancy. We give a general framework for designing consistent algorithms for such complex design goals by viewing the learning problem as an optimization problem over the set of feasible confusion matrices. We provide multiple instantiations of our framework under different assumptions on the performance metrics and constraints, and in each case show rates of convergence to the optimal (feasible) classifier (and thus asymptotic consistency). Experiments on a variety of multiclass classification tasks and fairness-constrained problems show that our algorithms compare favorably to the state-of-the-art baselines.

Statistical Guarantees for Fairness Aware Plug-In Algorithms

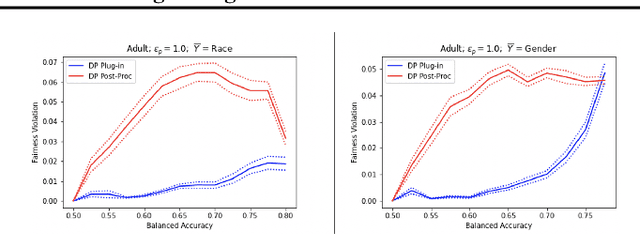
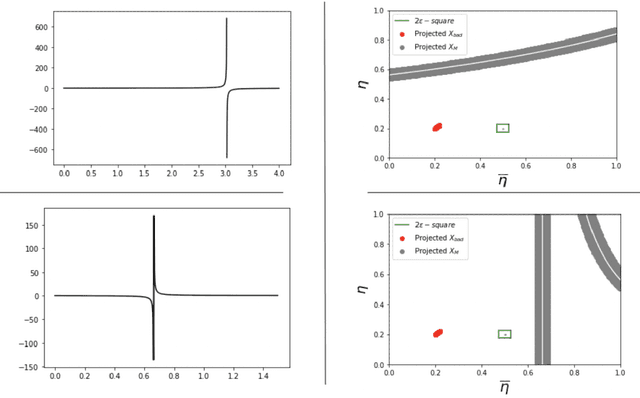
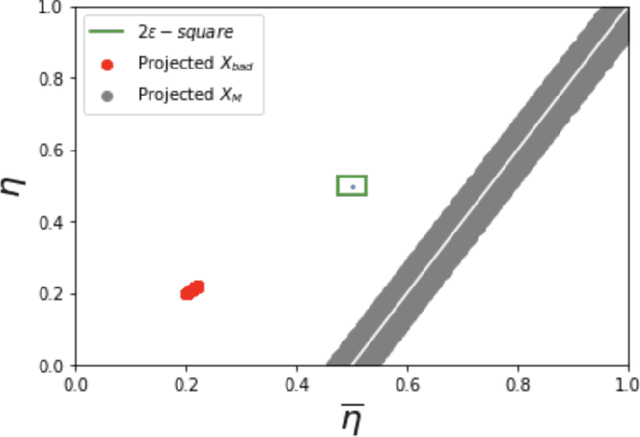
A plug-in algorithm to estimate Bayes Optimal Classifiers for fairness-aware binary classification has been proposed in (Menon & Williamson, 2018). However, the statistical efficacy of their approach has not been established. We prove that the plug-in algorithm is statistically consistent. We also derive finite sample guarantees associated with learning the Bayes Optimal Classifiers via the plug-in algorithm. Finally, we propose a protocol that modifies the plug-in approach, so as to simultaneously guarantee fairness and differential privacy with respect to a binary feature deemed sensitive.

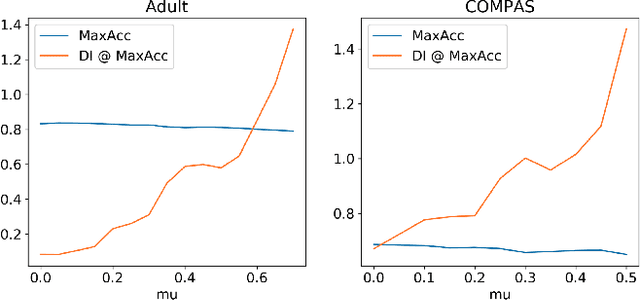
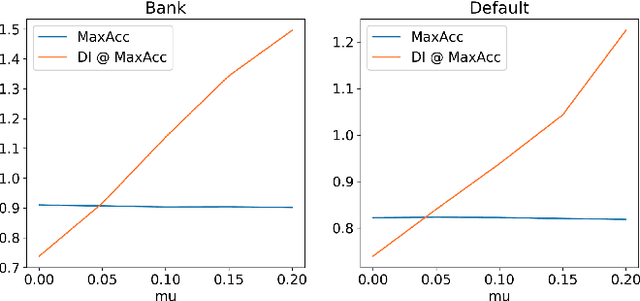
FairXGBoost: Fairness-aware Classification in XGBoost

Highly regulated domains such as finance have long favoured the use of machine learning algorithms that are scalable, transparent, robust and yield better performance. One of the most prominent examples of such an algorithm is XGBoost. Meanwhile, there is also a growing interest in building fair and unbiased models in these regulated domains and numerous bias-mitigation algorithms have been proposed to this end. However, most of these bias-mitigation methods are restricted to specific model families such as logistic regression or support vector machine models, thus leaving modelers with a difficult decision of choosing between fairness from the bias-mitigation algorithms and scalability, transparency, performance from algorithms such as XGBoost. We aim to leverage the best of both worlds by proposing a fair variant of XGBoost that enjoys all the advantages of XGBoost, while also matching the levels of fairness from the state-of-the-art bias-mitigation algorithms. Furthermore, the proposed solution requires very little in terms of changes to the original XGBoost library, thus making it easy for adoption. We provide an empirical analysis of our proposed method on standard benchmark datasets used in the fairness community.