The Space Complexity of Learning-Unlearning Algorithms

We study the memory complexity of machine unlearning algorithms that provide strong data deletion guarantees to the users. Formally, consider an algorithm for a particular learning task that initially receives a training dataset. Then, after learning, it receives data deletion requests from a subset of users (of arbitrary size), and the goal of unlearning is to perform the task as if the learner never received the data of deleted users. In this paper, we ask how many bits of storage are needed to be able to delete certain training samples at a later time. We focus on the task of realizability testing, where the goal is to check whether the remaining training samples are realizable within a given hypothesis class \(\mathcal{H}\). Toward that end, we first provide a negative result showing that the VC dimension is not a characterization of the space complexity of unlearning. In particular, we provide a hypothesis class with constant VC dimension (and Littlestone dimension), but for which any unlearning algorithm for realizability testing needs to store \(\Omega(n)\)-bits, where \(n\) denotes the size of the initial training dataset. In fact, we provide a stronger separation by showing that for any hypothesis class \(\mathcal{H}\), the amount of information that the learner needs to store, so as to perform unlearning later, is lower bounded by the \textit{eluder dimension} of \(\mathcal{H}\), a combinatorial notion always larger than the VC dimension. We complement the lower bound with an upper bound in terms of the star number of the underlying hypothesis class, albeit in a stronger ticketed-memory model proposed by Ghazi et al. (2023). Since the star number for a hypothesis class is never larger than its Eluder dimension, our work highlights a fundamental separation between central and ticketed memory models for machine unlearning.

Heavy-tailed Contamination is Easier than Adversarial Contamination

A large body of work in the statistics and computer science communities dating back to Huber (Huber, 1960) has led to statistically and computationally efficient outlier-robust estimators. Two particular outlier models have received significant attention: the adversarial and heavy-tailed models. While the former models outliers as the result of a malicious adversary manipulating the data, the latter relaxes distributional assumptions on the data allowing outliers to naturally occur as part of the data generating process. In the first setting, the goal is to develop estimators robust to the largest fraction of outliers while in the second, one seeks estimators to combat the loss of statistical efficiency, where the dependence on the failure probability is paramount. Despite these distinct motivations, the algorithmic approaches to both these settings have converged, prompting questions on the relationship between the models. In this paper, we investigate and provide a principled explanation for this phenomenon. First, we prove that any adversarially robust estimator is also resilient to heavy-tailed outliers for any statistical estimation problem with i.i.d data. As a corollary, optimal adversarially robust estimators for mean estimation, linear regression, and covariance estimation are also optimal heavy-tailed estimators. Conversely, for arguably the simplest high-dimensional estimation task of mean estimation, we construct heavy-tailed estimators whose application to the adversarial setting requires any black-box reduction to remove almost all the outliers in the data. Taken together, our results imply that heavy-tailed estimation is likely easier than adversarially robust estimation opening the door to novel algorithmic approaches for the heavy-tailed setting. Additionally, confidence intervals obtained for adversarially robust estimation also hold with high-probability.

How much is a noisy image worth? Data Scaling Laws for Ambient Diffusion

The quality of generative models depends on the quality of the data they are trained on. Creating large-scale, high-quality datasets is often expensive and sometimes impossible, e.g. in certain scientific applications where there is no access to clean data due to physical or instrumentation constraints. Ambient Diffusion and related frameworks train diffusion models with solely corrupted data (which are usually cheaper to acquire) but ambient models significantly underperform models trained on clean data. We study this phenomenon at scale by training more than $80$ models on data with different corruption levels across three datasets ranging from $30,000$ to $\approx 1.3$M samples. We show that it is impossible, at these sample sizes, to match the performance of models trained on clean data when only training on noisy data. Yet, a combination of a small set of clean data (e.g.~$10\%$ of the total dataset) and a large set of highly noisy data suffices to reach the performance of models trained solely on similar-size datasets of clean data, and in particular to achieve near state-of-the-art performance. We provide theoretical evidence for our findings by developing novel sample complexity bounds for learning from Gaussian Mixtures with heterogeneous variances. Our theoretical model suggests that, for large enough datasets, the effective marginal utility of a noisy sample is exponentially worse than that of a clean sample. Providing a small set of clean samples can significantly reduce the sample size requirements for noisy data, as we also observe in our experiments.

Mechanistic Interpretation through Contextual Decomposition in Transformers

Transformers exhibit impressive capabilities but are often regarded as black boxes due to challenges in understanding the complex nonlinear relationships between features. Interpreting machine learning models is of paramount importance to mitigate risks, and mechanistic interpretability is in particular of current interest as it opens up a window for guiding manual modifications and reverse-engineering solutions. In this work, we introduce contextual decomposition for transformers (CD-T), extending a prior work on CD for RNNs and CNNs, to address mechanistic interpretation computationally efficiently. CD-T is a flexible interpretation method for transformers. It can capture contributions of combinations of input features or source internal components (e.g. attention heads, feed-forward networks) to (1) final predictions or (2) the output of any target internal component. Using CD-T, we propose a novel algorithm for circuit discovery. On a real-world pathology report classification task: we show CD-T distills a more faithful circuit of attention heads with improved computational efficiency (speed up 2x) than a prior benchmark, path patching. As a versatile interpretation method, CD-T also exhibits exceptional capabilities for local interpretations. CD-T is shown to reliably find words and phrases of contrasting sentiment/topic on SST-2 and AGNews datasets. Through human experiments, we demonstrate CD-T enables users to identify the more accurate of two models and to better trust a model's outputs compared to alternative interpretation methods such as SHAP and LIME.

Statistical Barriers to Affine-equivariant Estimation

We investigate the quantitative performance of affine-equivariant estimators for robust mean estimation. As a natural stability requirement, the construction of such affine-equivariant estimators has been extensively studied in the statistics literature. We quantitatively evaluate these estimators under two outlier models which have been the subject of much recent work: the heavy-tailed and adversarial corruption settings. We establish lower bounds which show that affine-equivariance induces a strict degradation in recovery error with quantitative rates degrading by a factor of $\sqrt{d}$ in both settings. We find that classical estimators such as the Tukey median (Tukey '75) and Stahel-Donoho estimator (Stahel '81 and Donoho '82) are either quantitatively sub-optimal even within the class of affine-equivariant estimators or lack any quantitative guarantees. On the other hand, recent estimators with strong quantitative guarantees are not affine-equivariant or require additional distributional assumptions to achieve it. We remedy this by constructing a new affine-equivariant estimator which nearly matches our lower bound. Our estimator is based on a novel notion of a high-dimensional median which may be of independent interest. Notably, our results are applicable more broadly to any estimator whose performance is evaluated in the Mahalanobis norm which, for affine-equivariant estimators, corresponds to an evaluation in Euclidean norm on isotropic distributions.

An Investigation into the Effects of Pre-training Data Distributions for Pathology Report Classification

Pre-trained transformer models have demonstrated success across many natural language processing (NLP) tasks. In applying these models to the clinical domain, a prevailing assumption is that pre-training language models from scratch on large-scale biomedical data results in substantial improvements. We test this assumption with 4 pathology classification tasks on a corpus of 2907 prostate cancer pathology reports. We evaluate 5 transformer pre-trained models that are the same size but differ in pre-training corpora. Specifically, we analyze 3 categories of models: 1)General-domain: BERT and Turing Natural Language Representation (TNLR) models, which use general corpora for pre-training, 2)Mixed-domain: BioBERT which is obtained from BERT by including PubMed abstracts in pre-training and Clinical BioBERT which additionally includes MIMIC-III clinical notes and 3)Domain-specific: PubMedBERT which is pre-trained from scratch on PubMed abstracts. We find the mixed-domain and domain-specific models exhibit faster feature disambiguation during fine-tuning. However, the domain-specific model, PubMedBERT, can overfit to minority classes when presented with class imbalance, a common scenario in pathology report data. At the same time, the mixed-domain models are more resistant to overfitting. Our findings indicate that the use of general natural language and domain-specific corpora in pre-training serve complementary purposes for pathology report classification. The first enables resistance to overfitting when fine-tuning on an imbalanced dataset while the second allows for more accurate modelling of the fine-tuning domain. An expert evaluation is also conducted to reveal common outlier modes of each model. Our results could inform better fine-tuning practices in the clinical domain, to possibly leverage the benefits of mixed-domain models for imbalanced downstream datasets.

Optimal PAC Bounds Without Uniform Convergence

In statistical learning theory, determining the sample complexity of realizable binary classification for VC classes was a long-standing open problem. The results of Simon and Hanneke established sharp upper bounds in this setting. However, the reliance of their argument on the uniform convergence principle limits its applicability to more general learning settings such as multiclass classification. In this paper, we address this issue by providing optimal high probability risk bounds through a framework that surpasses the limitations of uniform convergence arguments. Our framework converts the leave-one-out error of permutation invariant predictors into high probability risk bounds. As an application, by adapting the one-inclusion graph algorithm of Haussler, Littlestone, and Warmuth, we propose an algorithm that achieves an optimal PAC bound for binary classification. Specifically, our result shows that certain aggregations of one-inclusion graph algorithms are optimal, addressing a variant of a classic question posed by Warmuth. We further instantiate our framework in three settings where uniform convergence is provably suboptimal. For multiclass classification, we prove an optimal risk bound that scales with the one-inclusion hypergraph density of the class, addressing the suboptimality of the analysis of Daniely and Shalev-Shwartz. For partial hypothesis classification, we determine the optimal sample complexity bound, resolving a question posed by Alon, Hanneke, Holzman, and Moran. For realizable bounded regression with absolute loss, we derive an optimal risk bound that relies on a modified version of the scale-sensitive dimension, refining the results of Bartlett and Long. Our rates surpass standard uniform convergence-based results due to the smaller complexity measure in our risk bound.

The One-Inclusion Graph Algorithm is not Always Optimal

The one-inclusion graph algorithm of Haussler, Littlestone, and Warmuth achieves an optimal in-expectation risk bound in the standard PAC classification setup. In one of the first COLT open problems, Warmuth conjectured that this prediction strategy always implies an optimal high probability bound on the risk, and hence is also an optimal PAC algorithm. We refute this conjecture in the strongest sense: for any practically interesting Vapnik-Chervonenkis class, we provide an in-expectation optimal one-inclusion graph algorithm whose high probability risk bound cannot go beyond that implied by Markov's inequality. Our construction of these poorly performing one-inclusion graph algorithms uses Varshamov-Tenengolts error correcting codes. Our negative result has several implications. First, it shows that the same poor high-probability performance is inherited by several recent prediction strategies based on generalizations of the one-inclusion graph algorithm. Second, our analysis shows yet another statistical problem that enjoys an estimator that is provably optimal in expectation via a leave-one-out argument, but fails in the high-probability regime. This discrepancy occurs despite the boundedness of the binary loss for which arguments based on concentration inequalities often provide sharp high probability risk bounds.

What Makes A Good Fisherman? Linear Regression under Self-Selection Bias

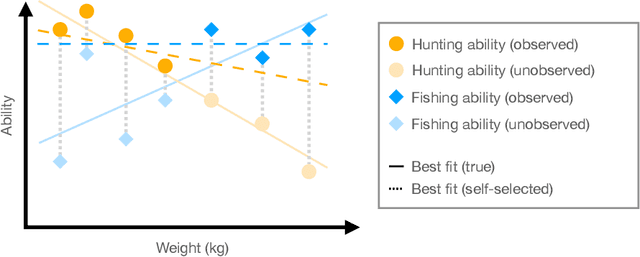
In the classical setting of self-selection, the goal is to learn $k$ models, simultaneously from observations $(x^{(i)}, y^{(i)})$ where $y^{(i)}$ is the output of one of $k$ underlying models on input $x^{(i)}$. In contrast to mixture models, where we observe the output of a randomly selected model, here the observed model depends on the outputs themselves, and is determined by some known selection criterion. For example, we might observe the highest output, the smallest output, or the median output of the $k$ models. In known-index self-selection, the identity of the observed model output is observable; in unknown-index self-selection, it is not. Self-selection has a long history in Econometrics and applications in various theoretical and applied fields, including treatment effect estimation, imitation learning, learning from strategically reported data, and learning from markets at disequilibrium. In this work, we present the first computationally and statistically efficient estimation algorithms for the most standard setting of this problem where the models are linear. In the known-index case, we require poly$(1/\varepsilon, k, d)$ sample and time complexity to estimate all model parameters to accuracy $\varepsilon$ in $d$ dimensions, and can accommodate quite general selection criteria. In the more challenging unknown-index case, even the identifiability of the linear models (from infinitely many samples) was not known. We show three results in this case for the commonly studied $\max$ self-selection criterion: (1) we show that the linear models are indeed identifiable, (2) for general $k$ we provide an algorithm with poly$(d) \exp(\text{poly}(k))$ sample and time complexity to estimate the regression parameters up to error $1/\text{poly}(k)$, and (3) for $k = 2$ we provide an algorithm for any error $\varepsilon$ and poly$(d, 1/\varepsilon)$ sample and time complexity.

Estimation of Standard Auction Models

We provide efficient estimation methods for first- and second-price auctions under independent (asymmetric) private values and partial observability. Given a finite set of observations, each comprising the identity of the winner and the price they paid in a sequence of identical auctions, we provide algorithms for non-parametrically estimating the bid distribution of each bidder, as well as their value distributions under equilibrium assumptions. We provide finite-sample estimation bounds which are uniform in that their error rates do not depend on the bid/value distributions being estimated. Our estimation guarantees advance a body of work in Econometrics wherein only identification results have been obtained, unless the setting is symmetric, parametric, or all bids are observable. Our guarantees also provide computationally and statistically effective alternatives to classical techniques from reliability theory. Finally, our results are immediately applicable to Dutch and English auctions.