Adaptive-Frequency Model Learning and Predictive Control for Dynamic Maneuvers on Legged Robots

Achieving both target accuracy and robustness in dynamic maneuvers with long flight phases, such as high or long jumps, has been a significant challenge for legged robots. To address this challenge, we propose a novel learning-based control approach consisting of model learning and model predictive control (MPC) utilizing an adaptive frequency scheme. Compared to existing MPC techniques, we learn a model directly from experiments, accounting not only for leg dynamics but also for modeling errors and unknown dynamics mismatch in hardware and during contact. Additionally, learning the model with adaptive frequency allows us to cover the entire flight phase and final jumping target, enhancing the prediction accuracy of the jumping trajectory. Using the learned model, we also design an adaptive-frequency MPC to effectively leverage different jumping phases and track the target accurately. In hardware experiments with a Unitree A1 robot, we demonstrate that our approach outperforms baseline MPC using a nominal model, reducing the jumping distance error up to 8 times. We achieve jumping distance errors of less than 3 percent during continuous jumping on uneven terrain with randomly-placed perturbations of random heights (up to 4 cm or 27 percent of the robot's standing height). Our approach obtains distance errors of 1-2 cm on 34 single and continuous jumps with different jumping targets and model uncertainties.

Port-Hamiltonian Neural ODE Networks on Lie Groups For Robot Dynamics Learning and Control

Accurate models of robot dynamics are critical for safe and stable control and generalization to novel operational conditions. Hand-designed models, however, may be insufficiently accurate, even after careful parameter tuning. This motivates the use of machine learning techniques to approximate the robot dynamics over a training set of state-control trajectories. The dynamics of many robots are described in terms of their generalized coordinates on a matrix Lie group, e.g. on SE(3) for ground, aerial, and underwater vehicles, and generalized velocity, and satisfy conservation of energy principles. This paper proposes a (port-)Hamiltonian formulation over a Lie group of the structure of a neural ordinary differential equation (ODE) network to approximate the robot dynamics. In contrast to a black-box ODE network, our formulation guarantees energy conservation principle and Lie group's constraints by construction and explicitly accounts for energy-dissipation effect such as friction and drag forces in the dynamics model. We develop energy shaping and damping injection control for the learned, potentially under-actuated Hamiltonian dynamics to enable a unified approach for stabilization and trajectory tracking with various robot platforms.

Physics-Informed Multi-Agent Reinforcement Learning for Distributed Multi-Robot Problems

The networked nature of multi-robot systems presents challenges in the context of multi-agent reinforcement learning. Centralized control policies do not scale with increasing numbers of robots, whereas independent control policies do not exploit the information provided by other robots, exhibiting poor performance in cooperative-competitive tasks. In this work we propose a physics-informed reinforcement learning approach able to learn distributed multi-robot control policies that are both scalable and make use of all the available information to each robot. Our approach has three key characteristics. First, it imposes a port-Hamiltonian structure on the policy representation, respecting energy conservation properties of physical robot systems and the networked nature of robot team interactions. Second, it uses self-attention to ensure a sparse policy representation able to handle time-varying information at each robot from the interaction graph. Third, we present a soft actor-critic reinforcement learning algorithm parameterized by our self-attention port-Hamiltonian control policy, which accounts for the correlation among robots during training while overcoming the need of value function factorization. Extensive simulations in different multi-robot scenarios demonstrate the success of the proposed approach, surpassing previous multi-robot reinforcement learning solutions in scalability, while achieving similar or superior performance (with averaged cumulative reward up to x2 greater than the state-of-the-art with robot teams x6 larger than the number of robots at training time).

Optimal Scene Graph Planning with Large Language Model Guidance

Recent advances in metric, semantic, and topological mapping have equipped autonomous robots with semantic concept grounding capabilities to interpret natural language tasks. This work aims to leverage these new capabilities with an efficient task planning algorithm for hierarchical metric-semantic models. We consider a scene graph representation of the environment and utilize a large language model (LLM) to convert a natural language task into a linear temporal logic (LTL) automaton. Our main contribution is to enable optimal hierarchical LTL planning with LLM guidance over scene graphs. To achieve efficiency, we construct a hierarchical planning domain that captures the attributes and connectivity of the scene graph and the task automaton, and provide semantic guidance via an LLM heuristic function. To guarantee optimality, we design an LTL heuristic function that is provably consistent and supplements the potentially inadmissible LLM guidance in multi-heuristic planning. We demonstrate efficient planning of complex natural language tasks in scene graphs of virtualized real environments.

Hamiltonian Dynamics Learning from Point Cloud Observations for Nonholonomic Mobile Robot Control

Reliable autonomous navigation requires adapting the control policy of a mobile robot in response to dynamics changes in different operational conditions. Hand-designed dynamics models may struggle to capture model variations due to a limited set of parameters. Data-driven dynamics learning approaches offer higher model capacity and better generalization but require large amounts of state-labeled data. This paper develops an approach for learning robot dynamics directly from point-cloud observations, removing the need and associated errors of state estimation, while embedding Hamiltonian structure in the dynamics model to improve data efficiency. We design an observation-space loss that relates motion prediction from the dynamics model with motion prediction from point-cloud registration to train a Hamiltonian neural ordinary differential equation. The learned Hamiltonian model enables the design of an energy-shaping model-based tracking controller for rigid-body robots. We demonstrate dynamics learning and tracking control on a real nonholonomic wheeled robot.

Learning to Identify Graphs from Node Trajectories in Multi-Robot Networks

The graph identification problem consists of discovering the interactions among nodes in a network given their state/feature trajectories. This problem is challenging because the behavior of a node is coupled to all the other nodes by the unknown interaction model. Besides, high-dimensional and nonlinear state trajectories make difficult to identify if two nodes are connected. Current solutions rely on prior knowledge of the graph topology and the dynamic behavior of the nodes, and hence, have poor generalization to other network configurations. To address these issues, we propose a novel learning-based approach that combines (i) a strongly convex program that efficiently uncovers graph topologies with global convergence guarantees and (ii) a self-attention encoder that learns to embed the original state trajectories into a feature space and predicts appropriate regularizers for the optimization program. In contrast to other works, our approach can identify the graph topology of unseen networks with new configurations in terms of number of nodes, connectivity or state trajectories. We demonstrate the effectiveness of our approach in identifying graphs in multi-robot formation and flocking tasks.

Lie Group Forced Variational Integrator Networks for Learning and Control of Robot Systems

Incorporating prior knowledge of physics laws and structural properties of dynamical systems into the design of deep learning architectures has proven to be a powerful technique for improving their computational efficiency and generalization capacity. Learning accurate models of robot dynamics is critical for safe and stable control. Autonomous mobile robots, including wheeled, aerial, and underwater vehicles, can be modeled as controlled Lagrangian or Hamiltonian rigid-body systems evolving on matrix Lie groups. In this paper, we introduce a new structure-preserving deep learning architecture, the Lie group Forced Variational Integrator Network (LieFVIN), capable of learning controlled Lagrangian or Hamiltonian dynamics on Lie groups, either from position-velocity or position-only data. By design, LieFVINs preserve both the Lie group structure on which the dynamics evolve and the symplectic structure underlying the Hamiltonian or Lagrangian systems of interest. The proposed architecture learns surrogate discrete-time flow maps allowing accurate and fast prediction without numerical-integrator, neural-ODE, or adjoint techniques, which are needed for vector fields. Furthermore, the learnt discrete-time dynamics can be utilized with computationally scalable discrete-time (optimal) control strategies.

LEMURS: Learning Distributed Multi-Robot Interactions

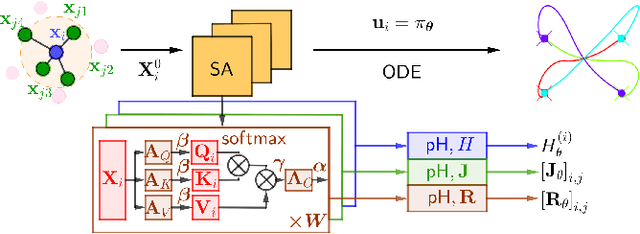
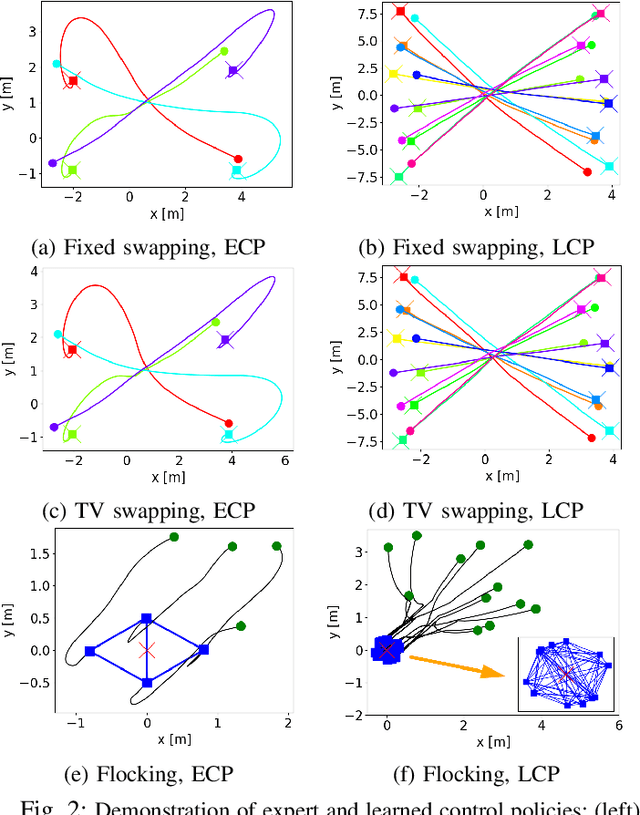
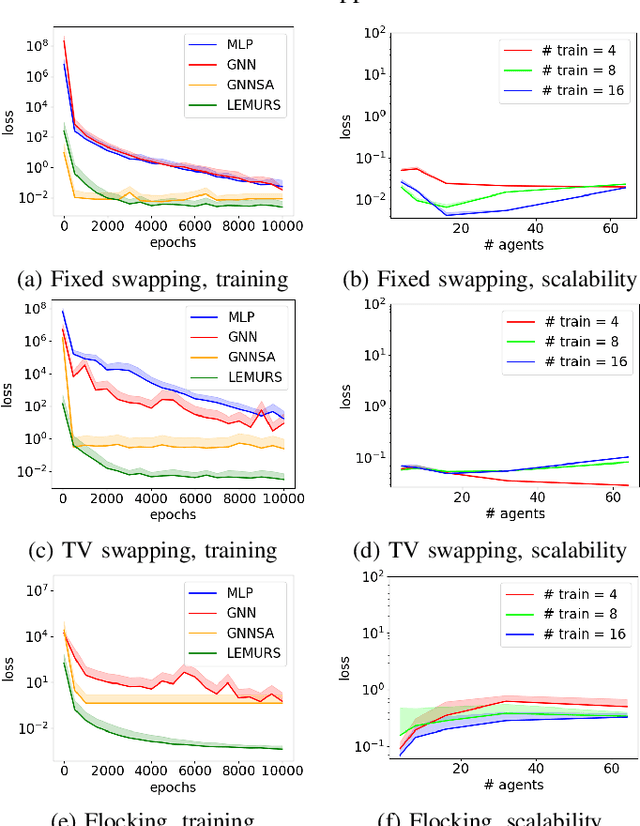
This paper presents LEMURS, an algorithm for learning scalable multi-robot control policies from cooperative task demonstrations. We propose a port-Hamiltonian description of the multi-robot system to exploit universal physical constraints in interconnected systems and achieve closed-loop stability. We represent a multi-robot control policy using an architecture that combines self-attention mechanisms and neural ordinary differential equations. The former handles time-varying communication in the robot team, while the latter respects the continuous-time robot dynamics. Our representation is distributed by construction, enabling the learned control policies to be deployed in robot teams of different sizes. We demonstrate that LEMURS can learn interactions and cooperative behaviors from demonstrations of multi-agent navigation and flocking tasks.

Robust and Safe Autonomous Navigation for Systems with Learned SE(3) Hamiltonian Dynamics

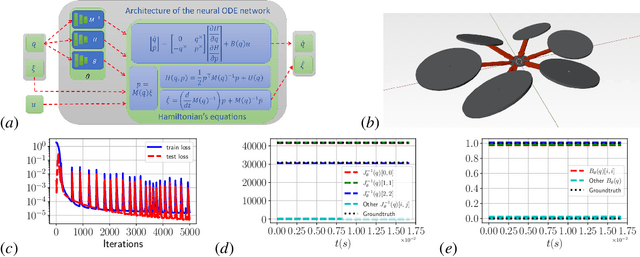
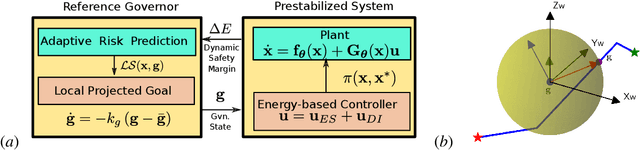
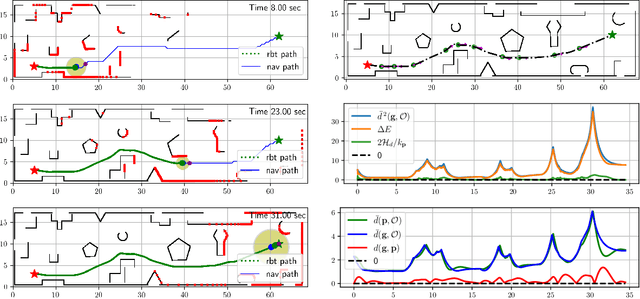
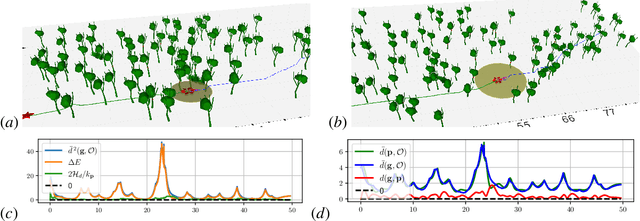
Stability and safety are critical properties for successful deployment of automatic control systems. As a motivating example, consider autonomous mobile robot navigation in a complex environment. A control design that generalizes to different operational conditions requires a model of the system dynamics, robustness to modeling errors, and satisfaction of safety \NEWZL{constraints}, such as collision avoidance. This paper develops a neural ordinary differential equation network to learn the dynamics of a Hamiltonian system from trajectory data. The learned Hamiltonian model is used to synthesize an energy-shaping passivity-based controller and analyze its \emph{robustness} to uncertainty in the learned model and its \emph{safety} with respect to constraints imposed by the environment. Given a desired reference path for the system, we extend our design using a virtual reference governor to achieve tracking control. The governor state serves as a regulation point that moves along the reference path adaptively, balancing the system energy level, model uncertainty bounds, and distance to safety violation to guarantee robustness and safety. Our Hamiltonian dynamics learning and tracking control techniques are demonstrated on \Revised{simulated hexarotor and quadrotor robots} navigating in cluttered 3D environments.

Physics-guided Learning-based Adaptive Control on the SE(3) Manifold

In real-world robotics applications, accurate models of robot dynamics are critical for safe and stable control in rapidly changing operational conditions. This motivates the use of machine learning techniques to approximate robot dynamics and their disturbances over a training set of state-control trajectories. This paper demonstrates that inductive biases arising from physics laws can be used to improve the data efficiency and accuracy of the approximated dynamics model. For example, the dynamics of many robots, including ground, aerial, and underwater vehicles, are described using their $SE(3)$ pose and satisfy conservation of energy principles. We design a physically plausible model of the robot dynamics by imposing the structure of Hamilton's equations of motion in the design of a neural ordinary differential equation (ODE) network. The Hamiltonian structure guarantees satisfaction of $SE(3)$ kinematic constraints and energy conservation by construction. It also allows us to derive an energy-based adaptive controller that achieves trajectory tracking while compensating for disturbances. Our learning-based adaptive controller is verified on an under-actuated quadrotor robot.