Neta Shaul
Corrector Sampling in Language Models
Jun 06, 2025

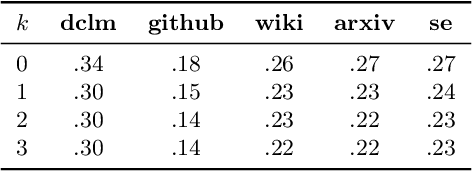
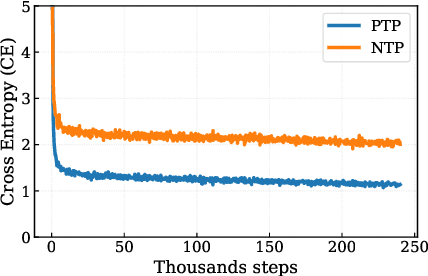
Abstract:Autoregressive language models accumulate errors due to their fixed, irrevocable left-to-right token generation. To address this, we propose a new sampling method called Resample-Previous-Tokens (RPT). RPT mitigates error accumulation by iteratively revisiting and potentially replacing tokens in a window of previously generated text. This method can be integrated into existing autoregressive models, preserving their next-token-prediction quality and speed. Fine-tuning a pretrained 8B parameter model with RPT for only 100B resulted in ~10% relative improvements on reasoning and coding benchmarks compared to the standard sampling.
Flow Matching Guide and Code
Dec 09, 2024Abstract:Flow Matching (FM) is a recent framework for generative modeling that has achieved state-of-the-art performance across various domains, including image, video, audio, speech, and biological structures. This guide offers a comprehensive and self-contained review of FM, covering its mathematical foundations, design choices, and extensions. By also providing a PyTorch package featuring relevant examples (e.g., image and text generation), this work aims to serve as a resource for both novice and experienced researchers interested in understanding, applying and further developing FM.
Flow Matching with General Discrete Paths: A Kinetic-Optimal Perspective
Dec 04, 2024Abstract:The design space of discrete-space diffusion or flow generative models are significantly less well-understood than their continuous-space counterparts, with many works focusing only on a simple masked construction. In this work, we aim to take a holistic approach to the construction of discrete generative models based on continuous-time Markov chains, and for the first time, allow the use of arbitrary discrete probability paths, or colloquially, corruption processes. Through the lens of optimizing the symmetric kinetic energy, we propose velocity formulas that can be applied to any given probability path, completely decoupling the probability and velocity, and giving the user the freedom to specify any desirable probability path based on expert knowledge specific to the data domain. Furthermore, we find that a special construction of mixture probability paths optimizes the symmetric kinetic energy for the discrete case. We empirically validate the usefulness of this new design space across multiple modalities: text generation, inorganic material generation, and image generation. We find that we can outperform the mask construction even in text with kinetic-optimal mixture paths, while we can make use of domain-specific constructions of the probability path over the visual domain.
Generator Matching: Generative modeling with arbitrary Markov processes
Oct 27, 2024



Abstract:We introduce generator matching, a modality-agnostic framework for generative modeling using arbitrary Markov processes. Generators characterize the infinitesimal evolution of a Markov process, which we leverage for generative modeling in a similar vein to flow matching: we construct conditional generators which generate single data points, then learn to approximate the marginal generator which generates the full data distribution. We show that generator matching unifies various generative modeling methods, including diffusion models, flow matching and discrete diffusion models. Furthermore, it provides the foundation to expand the design space to new and unexplored Markov processes such as jump processes. Finally, generator matching enables the construction of superpositions of Markov generative processes and enables the construction of multimodal models in a rigorous manner. We empirically validate our method on protein and image structure generation, showing that superposition with a jump process improves image generation.
Discrete Flow Matching
Jul 22, 2024Abstract:Despite Flow Matching and diffusion models having emerged as powerful generative paradigms for continuous variables such as images and videos, their application to high-dimensional discrete data, such as language, is still limited. In this work, we present Discrete Flow Matching, a novel discrete flow paradigm designed specifically for generating discrete data. Discrete Flow Matching offers several key contributions: (i) it works with a general family of probability paths interpolating between source and target distributions; (ii) it allows for a generic formula for sampling from these probability paths using learned posteriors such as the probability denoiser ($x$-prediction) and noise-prediction ($\epsilon$-prediction); (iii) practically, focusing on specific probability paths defined with different schedulers considerably improves generative perplexity compared to previous discrete diffusion and flow models; and (iv) by scaling Discrete Flow Matching models up to 1.7B parameters, we reach 6.7% Pass@1 and 13.4% Pass@10 on HumanEval and 6.7% Pass@1 and 20.6% Pass@10 on 1-shot MBPP coding benchmarks. Our approach is capable of generating high-quality discrete data in a non-autoregressive fashion, significantly closing the gap between autoregressive models and discrete flow models.
Bespoke Non-Stationary Solvers for Fast Sampling of Diffusion and Flow Models
Mar 02, 2024Abstract:This paper introduces Bespoke Non-Stationary (BNS) Solvers, a solver distillation approach to improve sample efficiency of Diffusion and Flow models. BNS solvers are based on a family of non-stationary solvers that provably subsumes existing numerical ODE solvers and consequently demonstrate considerable improvement in sample approximation (PSNR) over these baselines. Compared to model distillation, BNS solvers benefit from a tiny parameter space ($<$200 parameters), fast optimization (two orders of magnitude faster), maintain diversity of samples, and in contrast to previous solver distillation approaches nearly close the gap from standard distillation methods such as Progressive Distillation in the low-medium NFE regime. For example, BNS solver achieves 45 PSNR / 1.76 FID using 16 NFE in class-conditional ImageNet-64. We experimented with BNS solvers for conditional image generation, text-to-image generation, and text-2-audio generation showing significant improvement in sample approximation (PSNR) in all.
Guided Flows for Generative Modeling and Decision Making
Dec 07, 2023Abstract:Classifier-free guidance is a key component for enhancing the performance of conditional generative models across diverse tasks. While it has previously demonstrated remarkable improvements for the sample quality, it has only been exclusively employed for diffusion models. In this paper, we integrate classifier-free guidance into Flow Matching (FM) models, an alternative simulation-free approach that trains Continuous Normalizing Flows (CNFs) based on regressing vector fields. We explore the usage of \emph{Guided Flows} for a variety of downstream applications. We show that Guided Flows significantly improves the sample quality in conditional image generation and zero-shot text-to-speech synthesis, boasting state-of-the-art performance. Notably, we are the first to apply flow models for plan generation in the offline reinforcement learning setting, showcasing a 10x speedup in computation compared to diffusion models while maintaining comparable performance.
Bespoke Solvers for Generative Flow Models
Oct 29, 2023



Abstract:Diffusion or flow-based models are powerful generative paradigms that are notoriously hard to sample as samples are defined as solutions to high-dimensional Ordinary or Stochastic Differential Equations (ODEs/SDEs) which require a large Number of Function Evaluations (NFE) to approximate well. Existing methods to alleviate the costly sampling process include model distillation and designing dedicated ODE solvers. However, distillation is costly to train and sometimes can deteriorate quality, while dedicated solvers still require relatively large NFE to produce high quality samples. In this paper we introduce "Bespoke solvers", a novel framework for constructing custom ODE solvers tailored to the ODE of a given pre-trained flow model. Our approach optimizes an order consistent and parameter-efficient solver (e.g., with 80 learnable parameters), is trained for roughly 1% of the GPU time required for training the pre-trained model, and significantly improves approximation and generation quality compared to dedicated solvers. For example, a Bespoke solver for a CIFAR10 model produces samples with Fr\'echet Inception Distance (FID) of 2.73 with 10 NFE, and gets to 1% of the Ground Truth (GT) FID (2.59) for this model with only 20 NFE. On the more challenging ImageNet-64$\times$64, Bespoke samples at 2.2 FID with 10 NFE, and gets within 2% of GT FID (1.71) with 20 NFE.
On Kinetic Optimal Probability Paths for Generative Models
Jun 11, 2023Abstract:Recent successful generative models are trained by fitting a neural network to an a-priori defined tractable probability density path taking noise to training examples. In this paper we investigate the space of Gaussian probability paths, which includes diffusion paths as an instance, and look for an optimal member in some useful sense. In particular, minimizing the Kinetic Energy (KE) of a path is known to make particles' trajectories simple, hence easier to sample, and empirically improve performance in terms of likelihood of unseen data and sample generation quality. We investigate Kinetic Optimal (KO) Gaussian paths and offer the following observations: (i) We show the KE takes a simplified form on the space of Gaussian paths, where the data is incorporated only through a single, one dimensional scalar function, called the \emph{data separation function}. (ii) We characterize the KO solutions with a one dimensional ODE. (iii) We approximate data-dependent KO paths by approximating the data separation function and minimizing the KE. (iv) We prove that the data separation function converges to $1$ in the general case of arbitrary normalized dataset consisting of $n$ samples in $d$ dimension as $n/\sqrt{d}\rightarrow 0$. A consequence of this result is that the Conditional Optimal Transport (Cond-OT) path becomes \emph{kinetic optimal} as $n/\sqrt{d}\rightarrow 0$. We further support this theory with empirical experiments on ImageNet.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge