Set Block Decoding is a Language Model Inference Accelerator

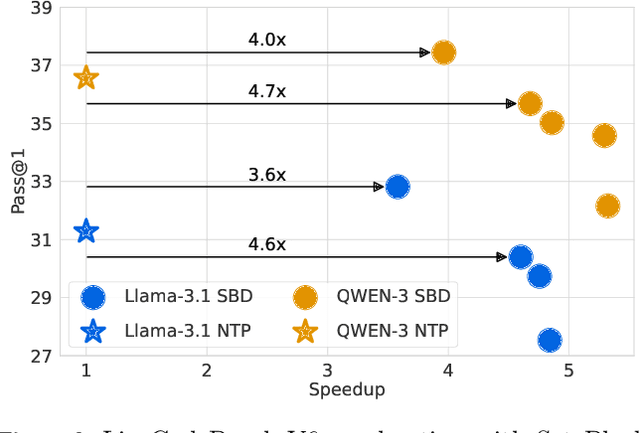
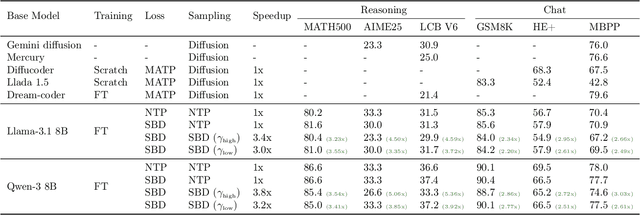
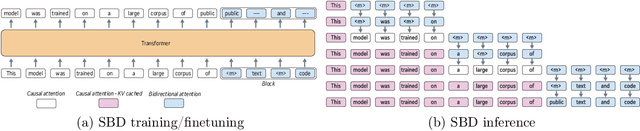
Autoregressive next token prediction language models offer powerful capabilities but face significant challenges in practical deployment due to the high computational and memory costs of inference, particularly during the decoding stage. We introduce Set Block Decoding (SBD), a simple and flexible paradigm that accelerates generation by integrating standard next token prediction (NTP) and masked token prediction (MATP) within a single architecture. SBD allows the model to sample multiple, not necessarily consecutive, future tokens in parallel, a key distinction from previous acceleration methods. This flexibility allows the use of advanced solvers from the discrete diffusion literature, offering significant speedups without sacrificing accuracy. SBD requires no architectural changes or extra training hyperparameters, maintains compatibility with exact KV-caching, and can be implemented by fine-tuning existing next token prediction models. By fine-tuning Llama-3.1 8B and Qwen-3 8B, we demonstrate that SBD enables a 3-5x reduction in the number of forward passes required for generation while achieving same performance as equivalent NTP training.

Accelerated Sampling from Masked Diffusion Models via Entropy Bounded Unmasking

Recent masked diffusion models (MDMs) have shown competitive performance compared to autoregressive models (ARMs) for language modeling. While most literature has focused on performance enhancing sampling procedures, efficient sampling from MDMs has been scarcely explored. We make the observation that often a given sequence of partially masked tokens determines the values of multiple unknown tokens deterministically, meaning that a single prediction of a masked model holds additional information unused by standard sampling procedures. Based on this observation, we introduce EB-Sampler, a simple drop-in replacement for existing samplers, utilizing an Entropy Bounded unmasking procedure that dynamically unmasks multiple tokens in one function evaluation with predefined approximate error tolerance. We formulate the EB-Sampler as part of a broad family of adaptive samplers for which we provide an error analysis that motivates our algorithmic choices. EB-Sampler accelerates sampling from current state of the art MDMs by roughly 2-3x on standard coding and math reasoning benchmarks without loss in performance. We also validate the same procedure works well on smaller reasoning tasks including maze navigation and Sudoku, tasks ARMs often struggle with.

Flow Matching Guide and Code

Flow Matching (FM) is a recent framework for generative modeling that has achieved state-of-the-art performance across various domains, including image, video, audio, speech, and biological structures. This guide offers a comprehensive and self-contained review of FM, covering its mathematical foundations, design choices, and extensions. By also providing a PyTorch package featuring relevant examples (e.g., image and text generation), this work aims to serve as a resource for both novice and experienced researchers interested in understanding, applying and further developing FM.

D-Flow: Differentiating through Flows for Controlled Generation

Taming the generation outcome of state of the art Diffusion and Flow-Matching (FM) models without having to re-train a task-specific model unlocks a powerful tool for solving inverse problems, conditional generation, and controlled generation in general. In this work we introduce D-Flow, a simple framework for controlling the generation process by differentiating through the flow, optimizing for the source (noise) point. We motivate this framework by our key observation stating that for Diffusion/FM models trained with Gaussian probability paths, differentiating through the generation process projects gradient on the data manifold, implicitly injecting the prior into the optimization process. We validate our framework on linear and non-linear controlled generation problems including: image and audio inverse problems and conditional molecule generation reaching state of the art performance across all.

Multisample Flow Matching: Straightening Flows with Minibatch Couplings

Simulation-free methods for training continuous-time generative models construct probability paths that go between noise distributions and individual data samples. Recent works, such as Flow Matching, derived paths that are optimal for each data sample. However, these algorithms rely on independent data and noise samples, and do not exploit underlying structure in the data distribution for constructing probability paths. We propose Multisample Flow Matching, a more general framework that uses non-trivial couplings between data and noise samples while satisfying the correct marginal constraints. At very small overhead costs, this generalization allows us to (i) reduce gradient variance during training, (ii) obtain straighter flows for the learned vector field, which allows us to generate high-quality samples using fewer function evaluations, and (iii) obtain transport maps with lower cost in high dimensions, which has applications beyond generative modeling. Importantly, we do so in a completely simulation-free manner with a simple minimization objective. We show that our proposed methods improve sample consistency on downsampled ImageNet data sets, and lead to better low-cost sample generation.

Flow Matching for Generative Modeling

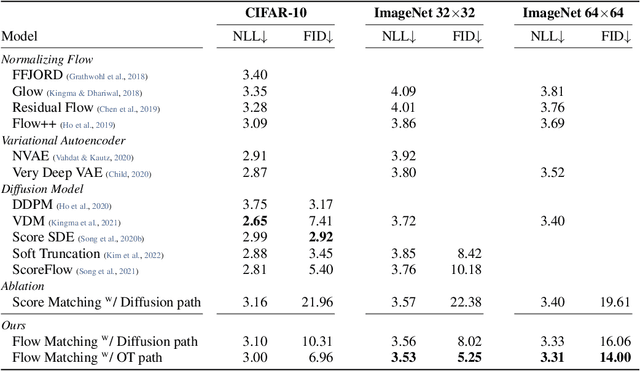
We introduce a new paradigm for generative modeling built on Continuous Normalizing Flows (CNFs), allowing us to train CNFs at unprecedented scale. Specifically, we present the notion of Flow Matching (FM), a simulation-free approach for training CNFs based on regressing vector fields of fixed conditional probability paths. Flow Matching is compatible with a general family of Gaussian probability paths for transforming between noise and data samples -- which subsumes existing diffusion paths as specific instances. Interestingly, we find that employing FM with diffusion paths results in a more robust and stable alternative for training diffusion models. Furthermore, Flow Matching opens the door to training CNFs with other, non-diffusion probability paths. An instance of particular interest is using Optimal Transport (OT) displacement interpolation to define the conditional probability paths. These paths are more efficient than diffusion paths, provide faster training and sampling, and result in better generalization. Training CNFs using Flow Matching on ImageNet leads to state-of-the-art performance in terms of both likelihood and sample quality, and allows fast and reliable sample generation using off-the-shelf numerical ODE solvers.

Matching Normalizing Flows and Probability Paths on Manifolds

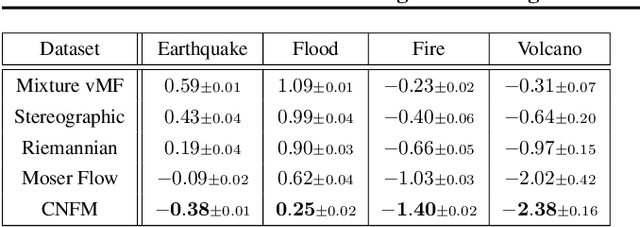
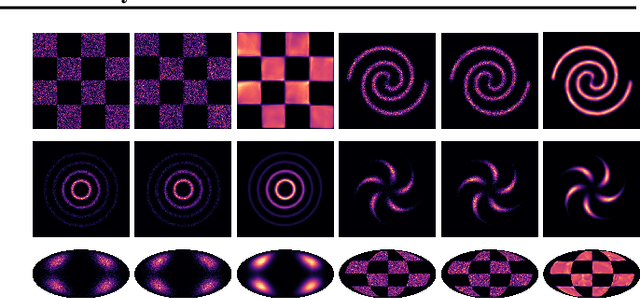
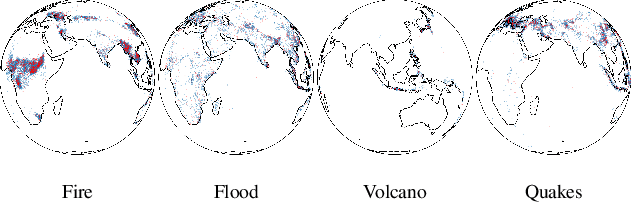
Continuous Normalizing Flows (CNFs) are a class of generative models that transform a prior distribution to a model distribution by solving an ordinary differential equation (ODE). We propose to train CNFs on manifolds by minimizing probability path divergence (PPD), a novel family of divergences between the probability density path generated by the CNF and a target probability density path. PPD is formulated using a logarithmic mass conservation formula which is a linear first order partial differential equation relating the log target probabilities and the CNF's defining vector field. PPD has several key benefits over existing methods: it sidesteps the need to solve an ODE per iteration, readily applies to manifold data, scales to high dimensions, and is compatible with a large family of target paths interpolating pure noise and data in finite time. Theoretically, PPD is shown to bound classical probability divergences. Empirically, we show that CNFs learned by minimizing PPD achieve state-of-the-art results in likelihoods and sample quality on existing low-dimensional manifold benchmarks, and is the first example of a generative model to scale to moderately high dimensional manifolds.

Frame Averaging for Invariant and Equivariant Network Design

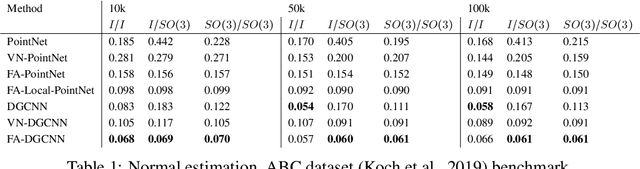
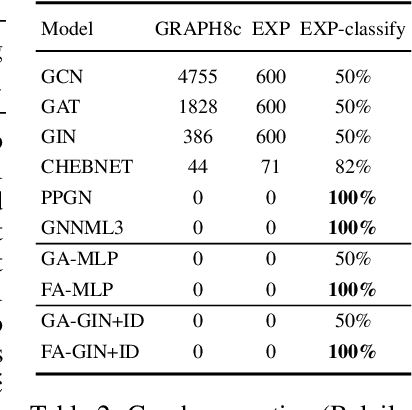
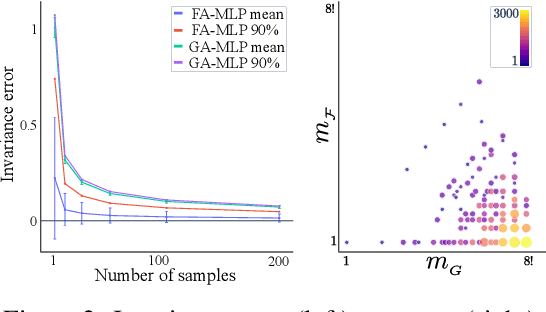
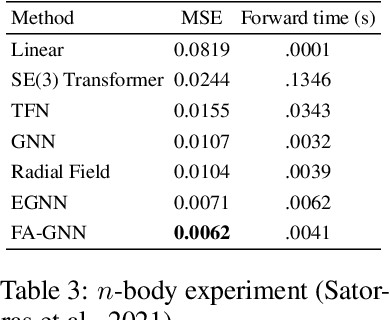
Many machine learning tasks involve learning functions that are known to be invariant or equivariant to certain symmetries of the input data. However, it is often challenging to design neural network architectures that respect these symmetries while being expressive and computationally efficient. For example, Euclidean motion invariant/equivariant graph or point cloud neural networks. We introduce Frame Averaging (FA), a general purpose and systematic framework for adapting known (backbone) architectures to become invariant or equivariant to new symmetry types. Our framework builds on the well known group averaging operator that guarantees invariance or equivariance but is intractable. In contrast, we observe that for many important classes of symmetries, this operator can be replaced with an averaging operator over a small subset of the group elements, called a frame. We show that averaging over a frame guarantees exact invariance or equivariance while often being much simpler to compute than averaging over the entire group. Furthermore, we prove that FA-based models have maximal expressive power in a broad setting and in general preserve the expressive power of their backbone architectures. Using frame averaging, we propose a new class of universal Graph Neural Networks (GNNs), universal Euclidean motion invariant point cloud networks, and Euclidean motion invariant Message Passing (MP) GNNs. We demonstrate the practical effectiveness of FA on several applications including point cloud normal estimation, beyond $2$-WL graph separation, and $n$-body dynamics prediction, achieving state-of-the-art results in all of these benchmarks.

From Graph Low-Rank Global Attention to 2-FWL Approximation

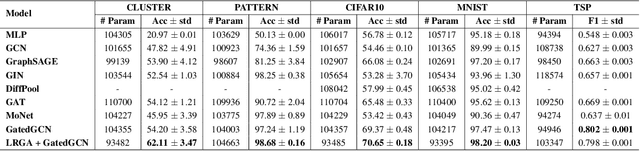
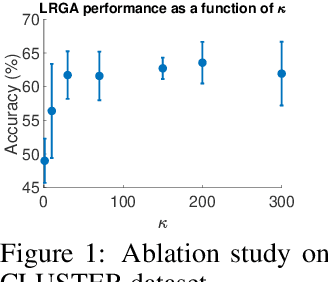
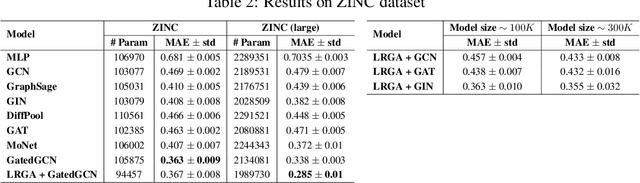
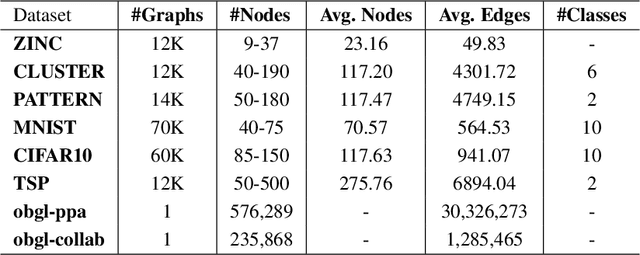
Graph Neural Networks (GNNs) are known to have an expressive power bounded by that of the vertex coloring algorithm (Xu et al., 2019a; Morris et al., 2018). However, for rich node features, such a bound does not exist and GNNs can be shown to be universal, namely, have the theoretical ability to approximate arbitrary graph functions. It is well known, however, that expressive power alone does not imply good generalization. In an effort to improve generalization of GNNs we suggest the Low-Rank Global Attention (LRGA) module, taking advantage of the efficiency of low rank matrix-vector multiplication, that improves the algorithmic alignment (Xu et al., 2019b) of GNNs with the 2-folklore Weisfeiler-Lehman (FWL) algorithm; 2-FWL is a graph isomorphism algorithm that is strictly more powerful than vertex coloring. Concretely, we: (i) formulate 2-FWL using polynomial kernels; (ii) show LRGA aligns with this 2-FWL formulation; and (iii) bound the sample complexity of the kernel's feature map when learned with a randomly initialized two-layer MLP. The latter means the generalization error can be made arbitrarily small when training LRGA to learn the 2-FWL algorithm. From a practical point of view, augmenting existing GNN layers with LRGA produces state of the art results on most datasets in a GNN standard benchmark.

Provably Powerful Graph Networks

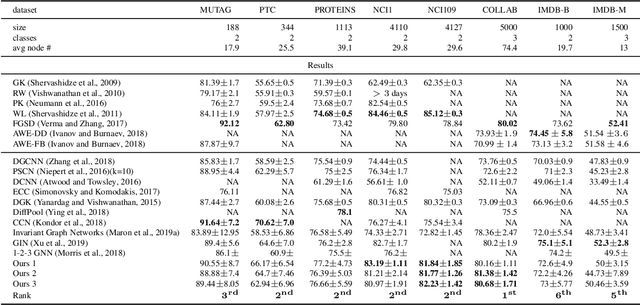
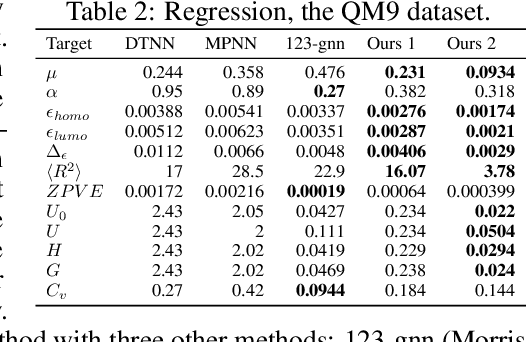
Recently, the Weisfeiler-Lehman (WL) graph isomorphism test was used to measure the expressive power of graph neural networks (GNN). It was shown that the popular message passing GNN cannot distinguish between graphs that are indistinguishable by the 1-WL test (Morris et al. 2018; Xu et al. 2019). Unfortunately, many simple instances of graphs are indistinguishable by the 1-WL test. In search for more expressive graph learning models we build upon the recent k-order invariant and equivariant graph neural networks (Maron et al. 2019a,b) and present two results: First, we show that such k-order networks can distinguish between non-isomorphic graphs as good as the k-WL tests, which are provably stronger than the 1-WL test for k>2. This makes these models strictly stronger than message passing models. Unfortunately, the higher expressiveness of these models comes with a computational cost of processing high order tensors. Second, setting our goal at building a provably stronger, simple and scalable model we show that a reduced 2-order network containing just scaled identity operator, augmented with a single quadratic operation (matrix multiplication) has a provable 3-WL expressive power. Differently put, we suggest a simple model that interleaves applications of standard Multilayer-Perceptron (MLP) applied to the feature dimension and matrix multiplication. We validate this model by presenting state of the art results on popular graph classification and regression tasks. To the best of our knowledge, this is the first practical invariant/equivariant model with guaranteed 3-WL expressiveness, strictly stronger than message passing models.