Minh Tang
Limit theorems for out-of-sample extensions of the adjacency and Laplacian spectral embeddings
Sep 29, 2019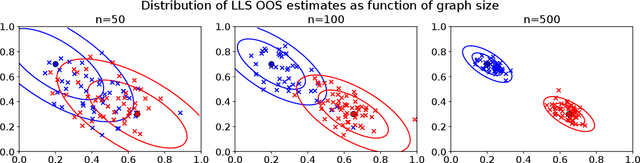
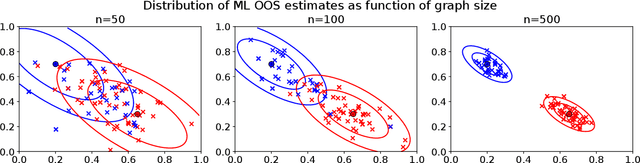
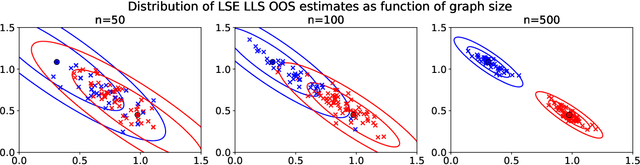
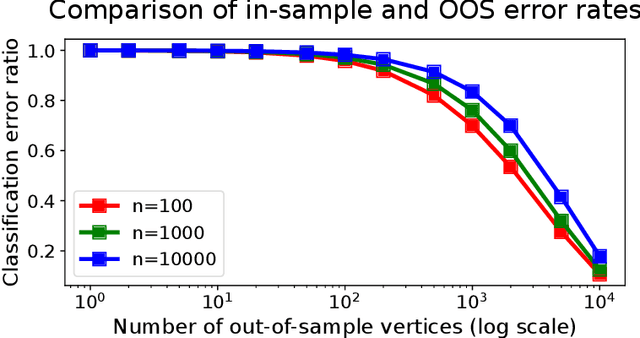
Abstract:Graph embeddings, a class of dimensionality reduction techniques designed for relational data, have proven useful in exploring and modeling network structure. Most dimensionality reduction methods allow out-of-sample extensions, by which an embedding can be applied to observations not present in the training set. Applied to graphs, the out-of-sample extension problem concerns how to compute the embedding of a vertex that is added to the graph after an embedding has already been computed. In this paper, we consider the out-of-sample extension problem for two graph embedding procedures: the adjacency spectral embedding and the Laplacian spectral embedding. In both cases, we prove that when the underlying graph is generated according to a latent space model called the random dot product graph, which includes the popular stochastic block model as a special case, an out-of-sample extension based on a least-squares objective obeys a central limit theorem about the true latent position of the out-of-sample vertex. In addition, we prove a concentration inequality for the out-of-sample extension of the adjacency spectral embedding based on a maximum-likelihood objective. Our results also yield a convenient framework in which to analyze trade-offs between estimation accuracy and computational expense, which we explore briefly.
On a 'Two Truths' Phenomenon in Spectral Graph Clustering
Sep 07, 2018
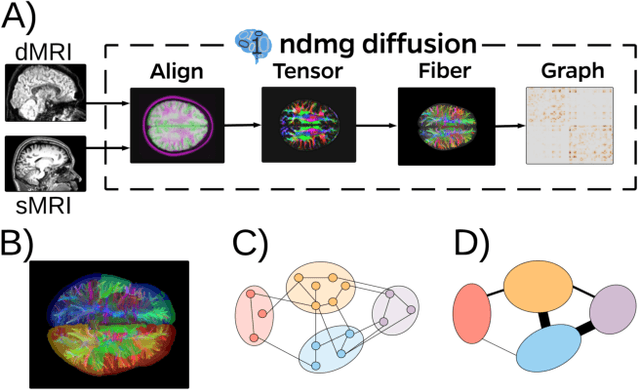
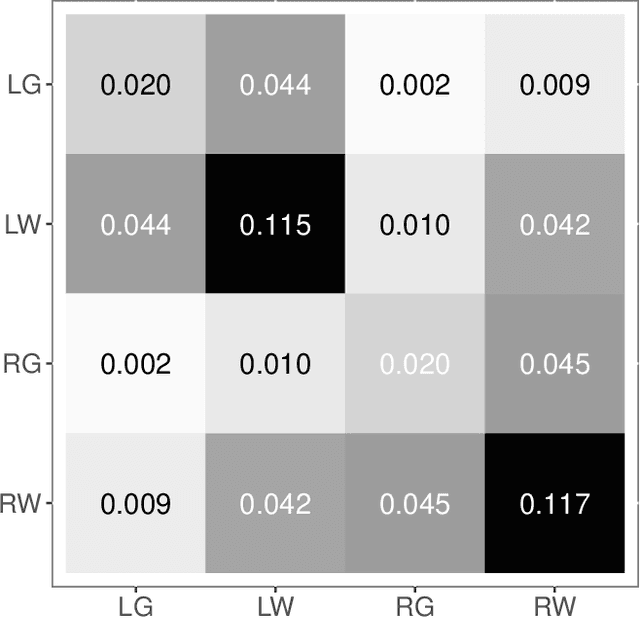
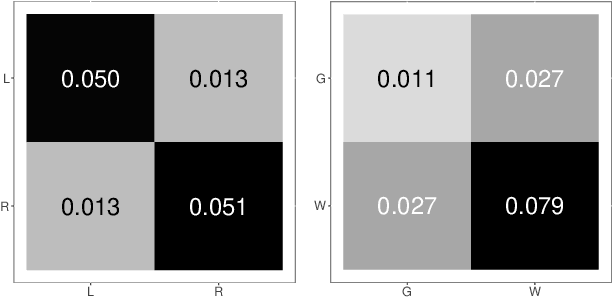
Abstract:Clustering is concerned with coherently grouping observations without any explicit concept of true groupings. Spectral graph clustering - clustering the vertices of a graph based on their spectral embedding - is commonly approached via K-means (or, more generally, Gaussian mixture model) clustering composed with either Laplacian or Adjacency spectral embedding (LSE or ASE). Recent theoretical results provide new understanding of the problem and solutions, and lead us to a 'Two Truths' LSE vs. ASE spectral graph clustering phenomenon convincingly illustrated here via a diffusion MRI connectome data set: the different embedding methods yield different clustering results, with LSE capturing left hemisphere/right hemisphere affinity structure and ASE capturing gray matter/white matter core-periphery structure.
A statistical interpretation of spectral embedding: the generalised random dot product graph
Jul 29, 2018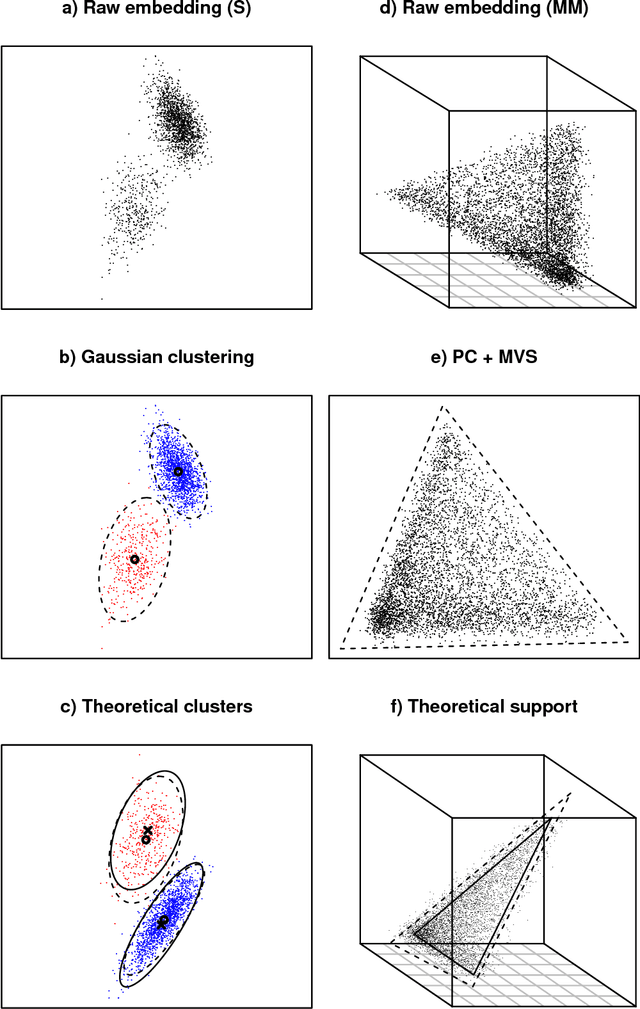
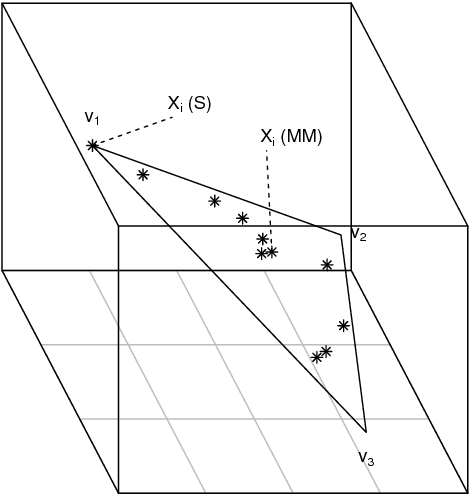
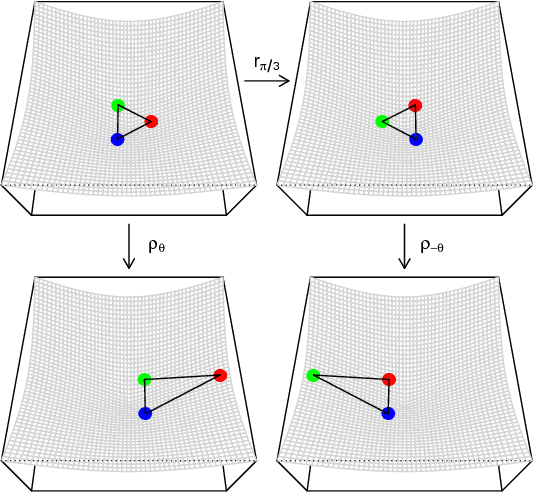

Abstract:A generalisation of a latent position network model known as the random dot product graph model is considered. The resulting model may be of independent interest because it has the unique property of representing a mixture of connectivity behaviours as the corresponding convex combination in latent space. We show that, whether the normalised Laplacian or adjacency matrix is used, the vector representations of nodes obtained by spectral embedding provide strongly consistent latent position estimates with asymptotically Gaussian error. Direct methodological consequences follow from the observation that the well-known mixed membership and standard stochastic block models are special cases where the latent positions live respectively inside or on the vertices of a simplex. Estimation via spectral embedding can therefore be achieved by respectively estimating this simplicial support, or fitting a Gaussian mixture model. In the latter case, the use of $K$-means, as has been previously recommended, is suboptimal and for identifiability reasons unsound. Empirical improvements in link prediction, as well as the potential to uncover much richer latent structure (than available under the mixed membership or standard stochastic block models) are demonstrated in a cyber-security example.
The eigenvalues of stochastic blockmodel graphs
Mar 30, 2018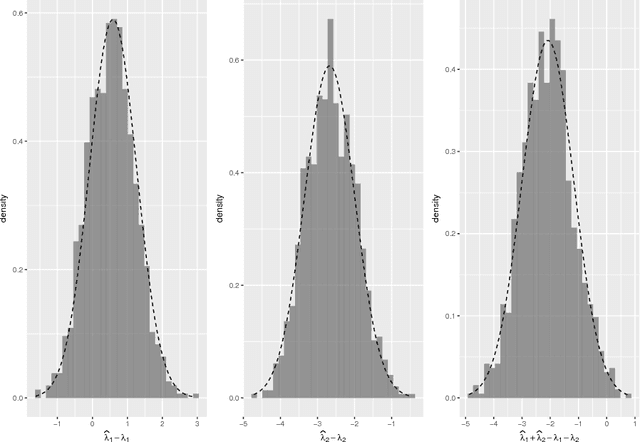
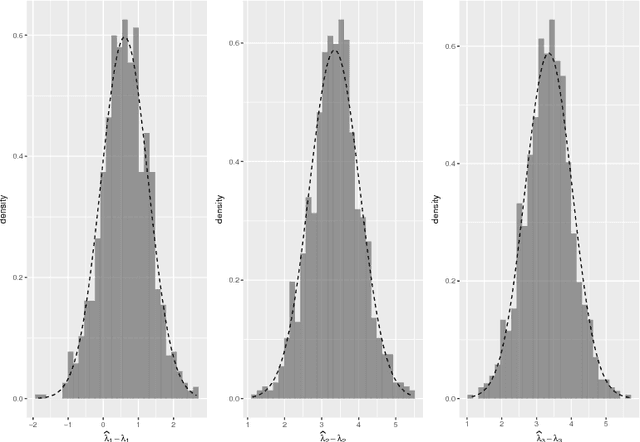
Abstract:We derive the limiting distribution for the largest eigenvalues of the adjacency matrix for a stochastic blockmodel graph when the number of vertices tends to infinity. We show that, in the limit, these eigenvalues are jointly multivariate normal with bounded covariances. Our result extends the classic result of F\"{u}redi and Koml\'{o}s on the fluctuation of the largest eigenvalue for Erd\H{o}s-R\'{e}nyi graphs.
Linear Optimal Low Rank Projection for High-Dimensional Multi-Class Data
Feb 27, 2018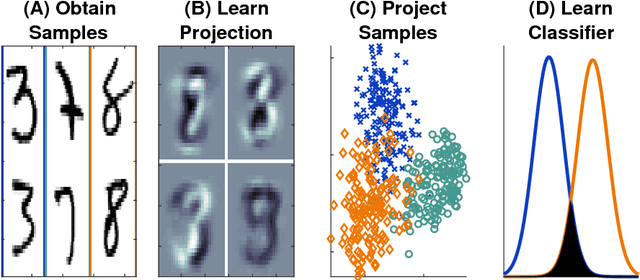
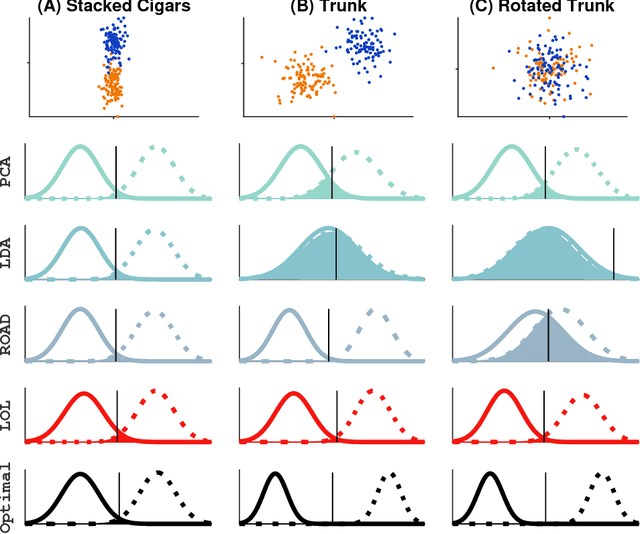
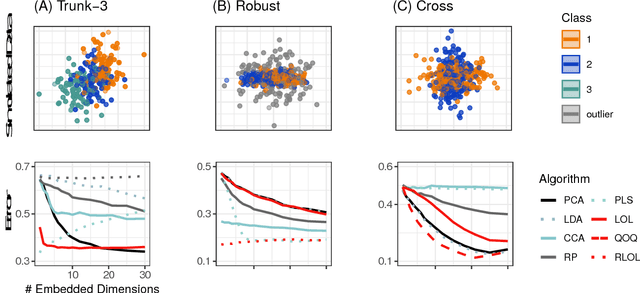
Abstract:Classifying samples into categories becomes intractable when a single sample can have millions to billions of features, such as in genetics or imaging data. Principal Components Analysis (PCA) is widely used to identify a low-dimensional representation of such features for further analysis. However, PCA ignores class labels, such as whether or not a subject has cancer, thereby discarding information that could substantially improve downstream classification performance. We describe an approach, "Linear Optimal Low-rank" projection (LOL), which extends PCA by incorporating the class labels in a fashion that is advantageous over existing supervised dimensionality reduction techniques. We prove, and substantiate with synthetic experiments, that LOL leads to a better representation of the data for subsequent classification than other linear approaches, while adding negligible computational cost. We then demonstrate that LOL substantially outperforms PCA in differentiating cancer patients from healthy controls using genetic data, and in differentiating gender using magnetic resonance imaging data with $>$500 million features and 400 gigabytes of data. LOL therefore allows the solution of previous intractable problems, yet requires only a few minutes to run on a desktop computer.
Statistical inference on random dot product graphs: a survey
Sep 16, 2017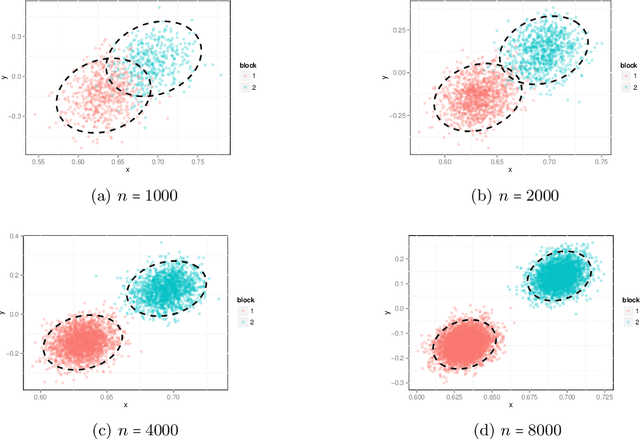
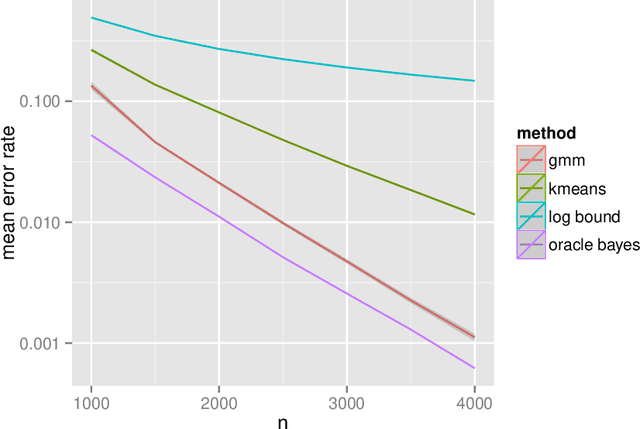

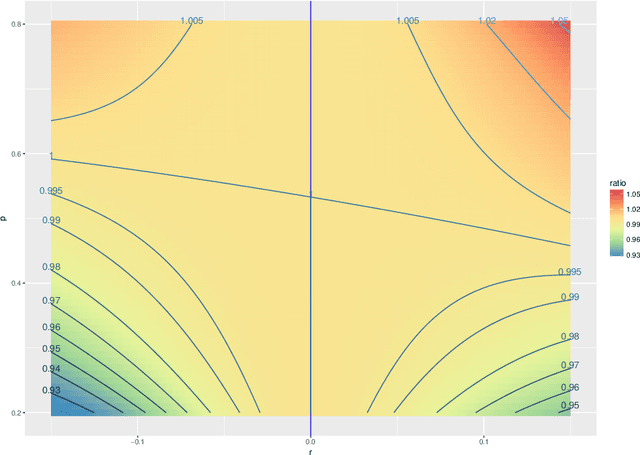
Abstract:The random dot product graph (RDPG) is an independent-edge random graph that is analytically tractable and, simultaneously, either encompasses or can successfully approximate a wide range of random graphs, from relatively simple stochastic block models to complex latent position graphs. In this survey paper, we describe a comprehensive paradigm for statistical inference on random dot product graphs, a paradigm centered on spectral embeddings of adjacency and Laplacian matrices. We examine the analogues, in graph inference, of several canonical tenets of classical Euclidean inference: in particular, we summarize a body of existing results on the consistency and asymptotic normality of the adjacency and Laplacian spectral embeddings, and the role these spectral embeddings can play in the construction of single- and multi-sample hypothesis tests for graph data. We investigate several real-world applications, including community detection and classification in large social networks and the determination of functional and biologically relevant network properties from an exploratory data analysis of the Drosophila connectome. We outline requisite background and current open problems in spectral graph inference.
* An expository survey paper on a comprehensive paradigm for inference for random dot product graphs, centered on graph adjacency and Laplacian spectral embeddings. Paper outlines requisite background; summarizes theory, methodology, and applications from previous and ongoing work; and closes with a discussion of several open problems
Semiparametric spectral modeling of the Drosophila connectome
May 09, 2017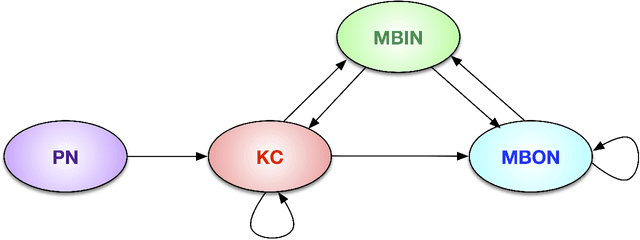
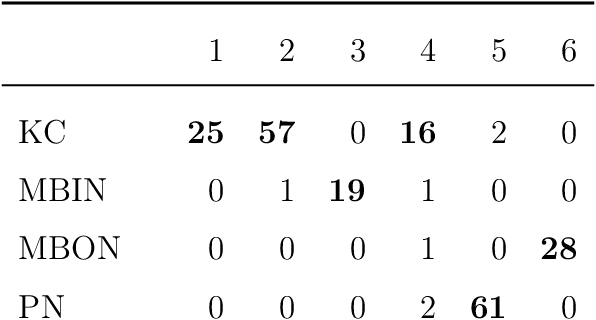
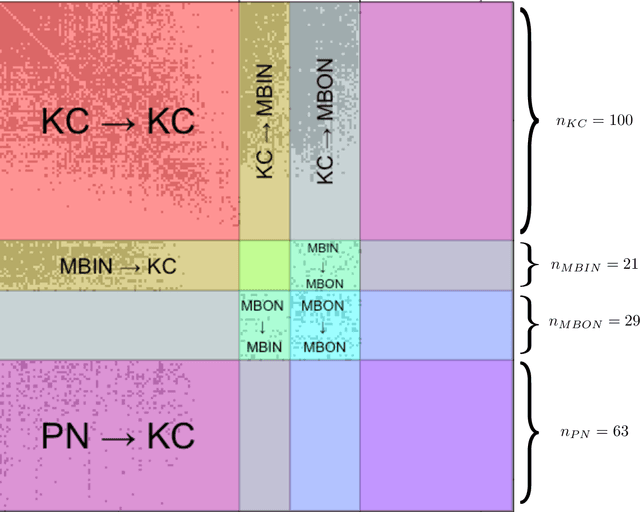

Abstract:We present semiparametric spectral modeling of the complete larval Drosophila mushroom body connectome. Motivated by a thorough exploratory data analysis of the network via Gaussian mixture modeling (GMM) in the adjacency spectral embedding (ASE) representation space, we introduce the latent structure model (LSM) for network modeling and inference. LSM is a generalization of the stochastic block model (SBM) and a special case of the random dot product graph (RDPG) latent position model, and is amenable to semiparametric GMM in the ASE representation space. The resulting connectome code derived via semiparametric GMM composed with ASE captures latent connectome structure and elucidates biologically relevant neuronal properties.
Community Detection and Classification in Hierarchical Stochastic Blockmodels
Aug 26, 2016
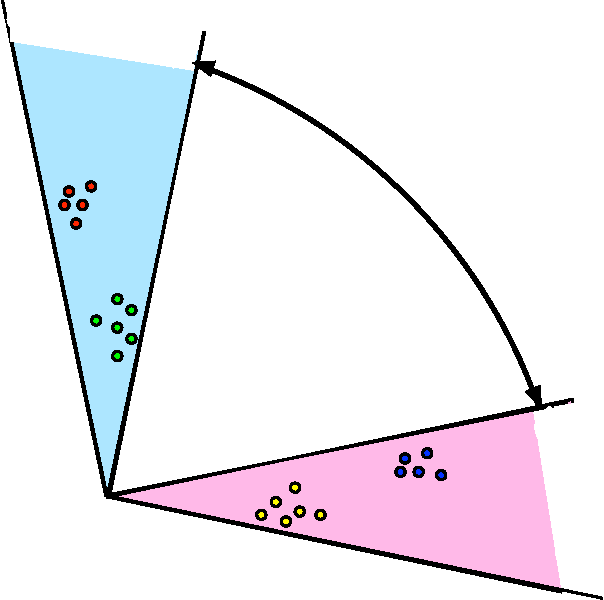
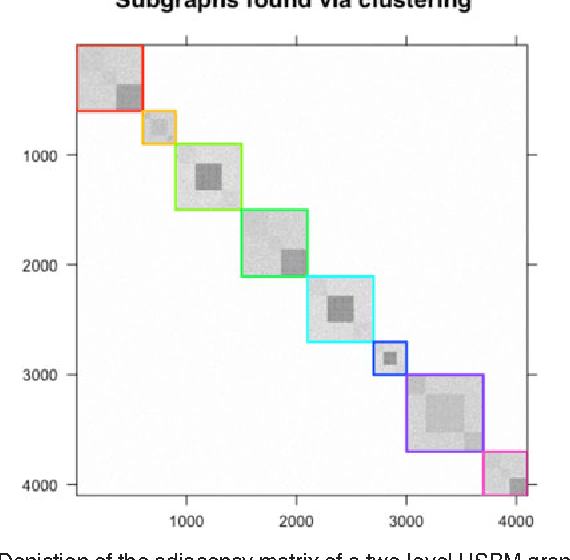
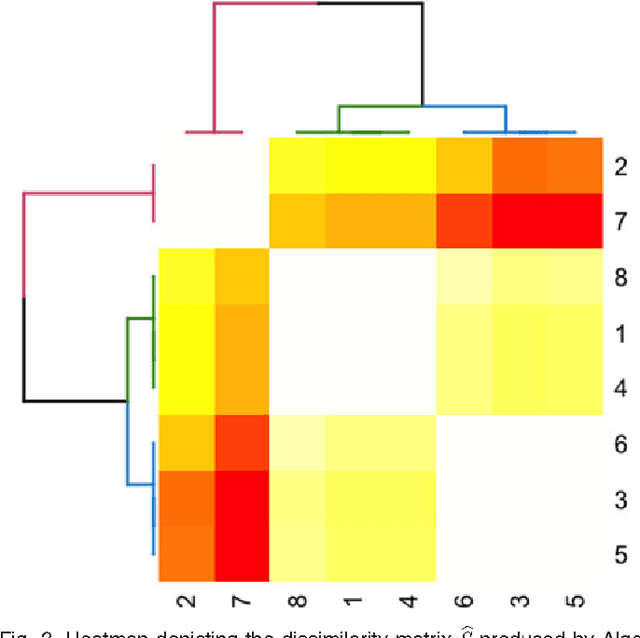
Abstract:We propose a robust, scalable, integrated methodology for community detection and community comparison in graphs. In our procedure, we first embed a graph into an appropriate Euclidean space to obtain a low-dimensional representation, and then cluster the vertices into communities. We next employ nonparametric graph inference techniques to identify structural similarity among these communities. These two steps are then applied recursively on the communities, allowing us to detect more fine-grained structure. We describe a hierarchical stochastic blockmodel---namely, a stochastic blockmodel with a natural hierarchical structure---and establish conditions under which our algorithm yields consistent estimates of model parameters and motifs, which we define to be stochastically similar groups of subgraphs. Finally, we demonstrate the effectiveness of our algorithm in both simulated and real data. Specifically, we address the problem of locating similar subcommunities in a partially reconstructed Drosophila connectome and in the social network Friendster.
Limit theorems for eigenvectors of the normalized Laplacian for random graphs
Jul 28, 2016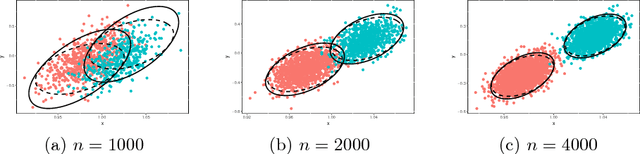
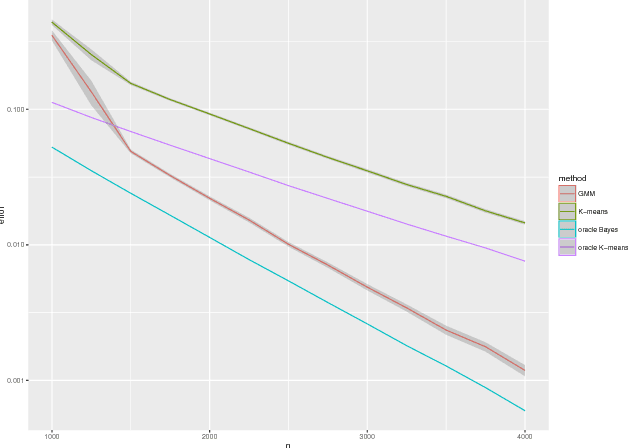
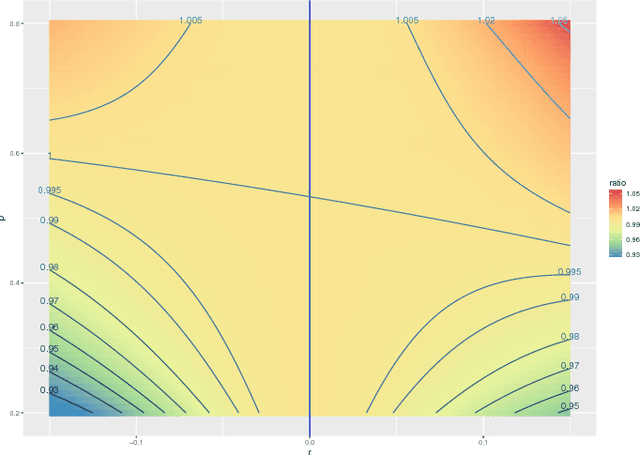
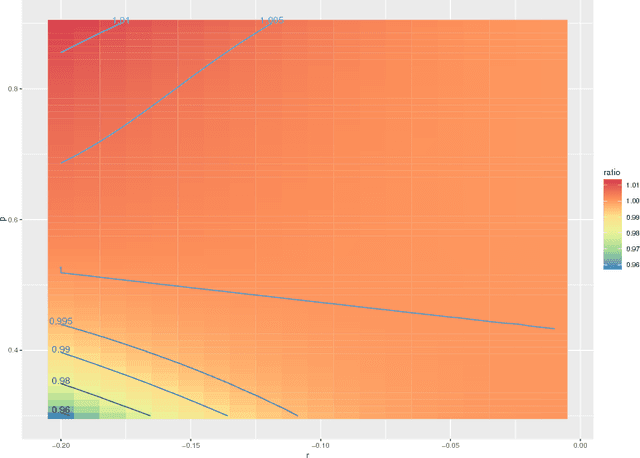
Abstract:We prove a central limit theorem for the components of the eigenvectors corresponding to the $d$ largest eigenvalues of the normalized Laplacian matrix of a finite dimensional random dot product graph. As a corollary, we show that for stochastic blockmodel graphs, the rows of the spectral embedding of the normalized Laplacian converge to multivariate normals and furthermore the mean and the covariance matrix of each row are functions of the associated vertex's block membership. Together with prior results for the eigenvectors of the adjacency matrix, we then compare, via the Chernoff information between multivariate normal distributions, how the choice of embedding method impacts subsequent inference. We demonstrate that neither embedding method dominates with respect to the inference task of recovering the latent block assignments.
Empirical Bayes Estimation for the Stochastic Blockmodel
Feb 09, 2016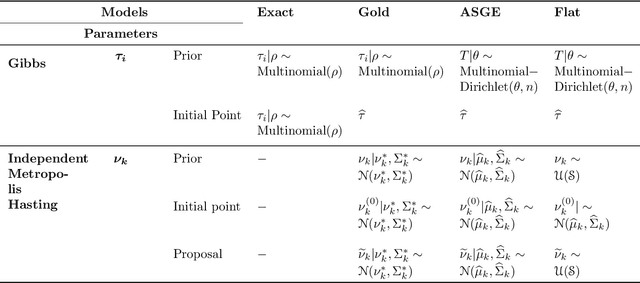
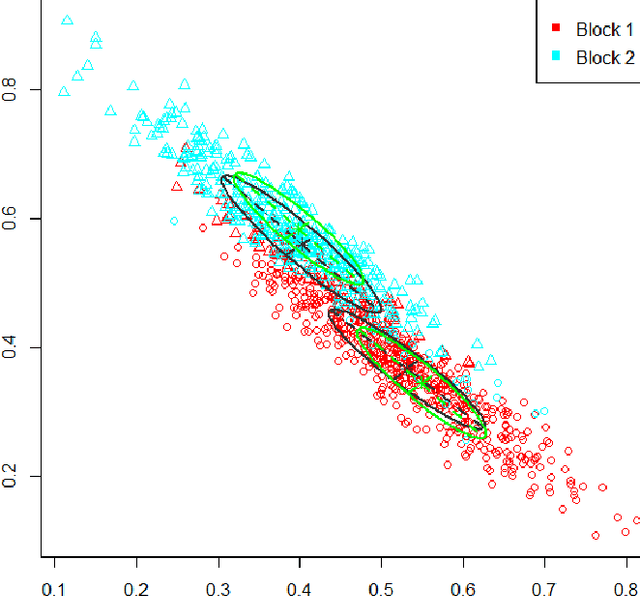
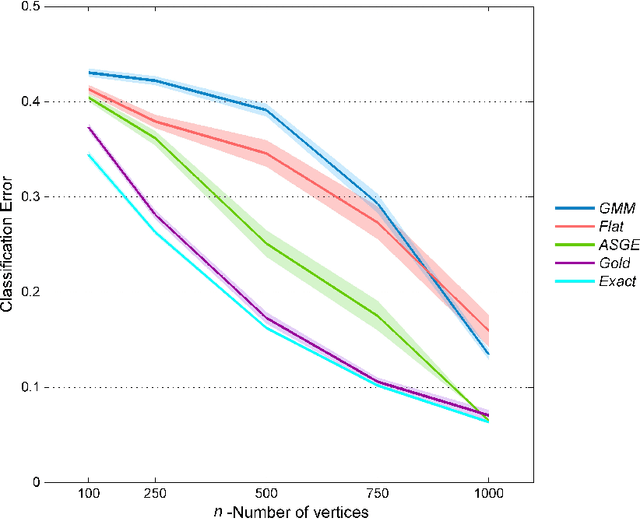
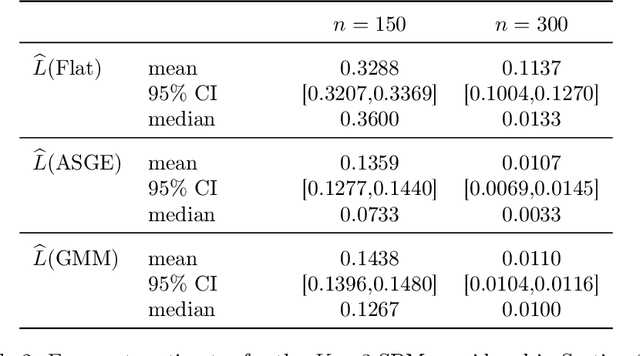
Abstract:Inference for the stochastic blockmodel is currently of burgeoning interest in the statistical community, as well as in various application domains as diverse as social networks, citation networks, brain connectivity networks (connectomics), etc. Recent theoretical developments have shown that spectral embedding of graphs yields tractable distributional results; in particular, a random dot product latent position graph formulation of the stochastic blockmodel informs a mixture of normal distributions for the adjacency spectral embedding. We employ this new theory to provide an empirical Bayes methodology for estimation of block memberships of vertices in a random graph drawn from the stochastic blockmodel, and demonstrate its practical utility. The posterior inference is conducted using a Metropolis-within-Gibbs algorithm. The theory and methods are illustrated through Monte Carlo simulation studies, both within the stochastic blockmodel and beyond, and experimental results on a Wikipedia data set are presented.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge