Keith Levin
Testing for correlation between network structure and high-dimensional node covariates
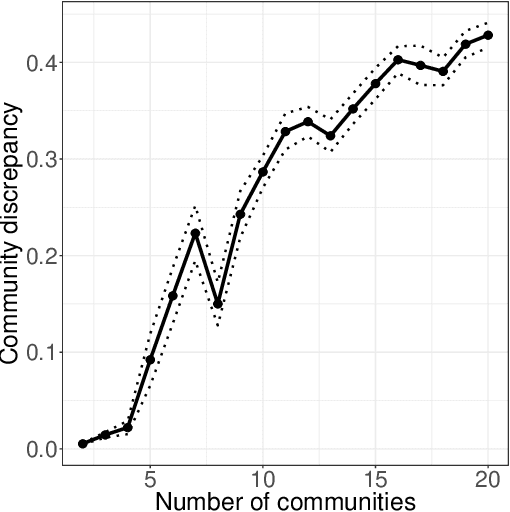
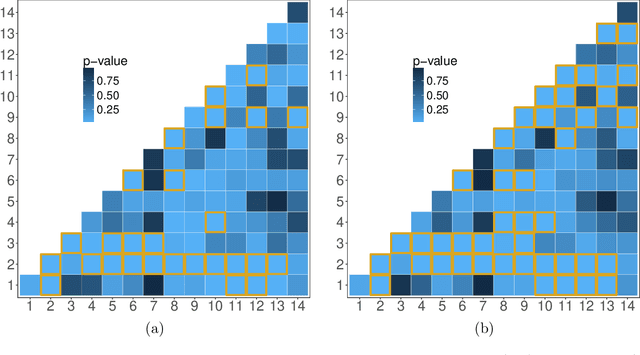
Sep 03, 2025Abstract:In many application domains, networks are observed with node-level features. In such settings, a common problem is to assess whether or not nodal covariates are correlated with the network structure itself. Here, we present four novel methods for addressing this problem. Two of these are based on a linear model relating node-level covariates to latent node-level variables that drive network structure. The other two are based on applying canonical correlation analysis to the node features and network structure, avoiding the linear modeling assumptions. We provide theoretical guarantees for all four methods when the observed network is generated according to a low-rank latent space model endowed with node-level covariates, which we allow to be high-dimensional. Our methods are computationally cheaper and require fewer modeling assumptions than previous approaches to network dependency testing. We demonstrate and compare the performance of our novel methods on both simulated and real-world data.
On the role of features in vertex nomination: Content and context together are better
May 06, 2020
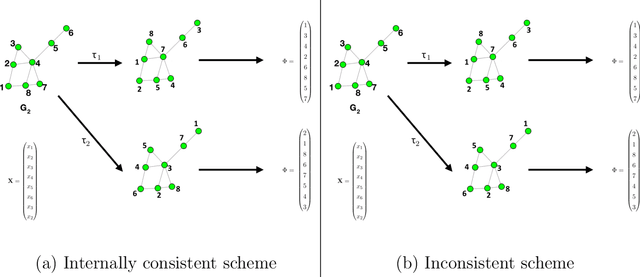
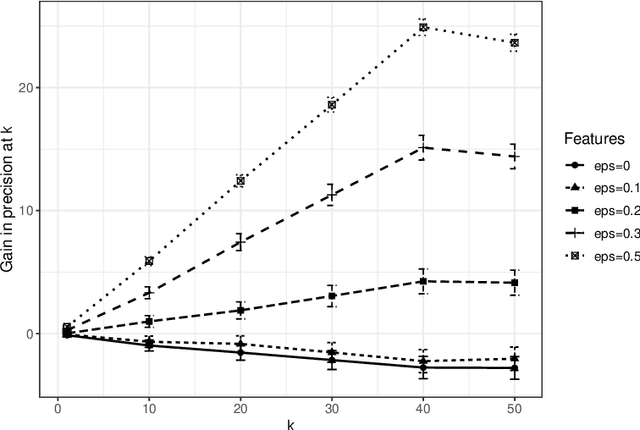

Abstract:Vertex nomination is a lightly-supervised network information retrieval (IR) task in which vertices of interest in one graph are used to query a second graph to discover vertices of interest in the second graph. Similar to other IR tasks, the output of a vertex nomination scheme is a ranked list of the vertices in the second graph, with the heretofore unknown vertices of interest ideally concentrating at the top of the list. Vertex nomination schemes provide a useful suite of tools for efficiently mining complex networks for pertinent information. In this paper, we explore, both theoretically and practically, the dual roles of content (i.e., edge and vertex attributes) and context (i.e., network topology) in vertex nomination. We provide necessary and sufficient conditions under which vertex nomination schemes that leverage both content and context outperform schemes that leverage only content or context separately. While the joint utility of both content and context has been demonstrated empirically in the literature, the framework presented in this paper provides a novel theoretical basis for understanding the potential complementary roles of network features and topology.
Limit theorems for out-of-sample extensions of the adjacency and Laplacian spectral embeddings
Sep 29, 2019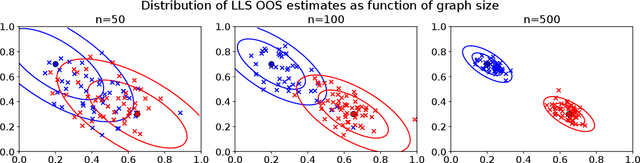
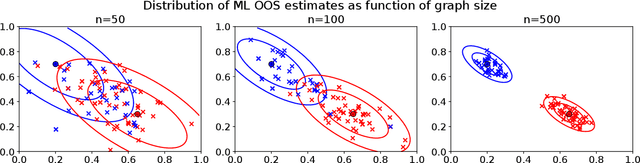
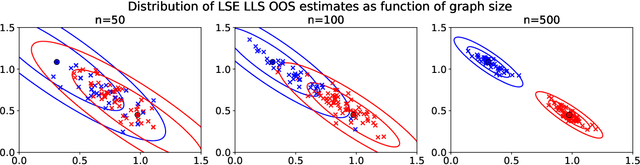
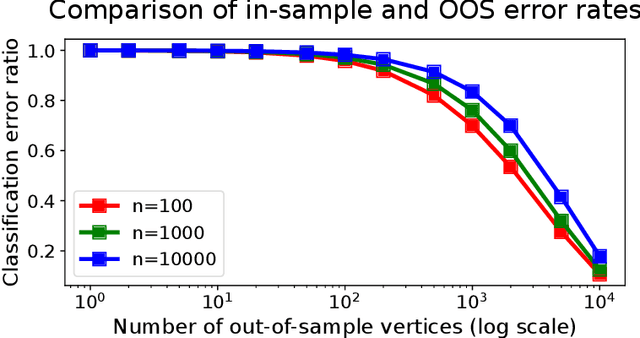
Abstract:Graph embeddings, a class of dimensionality reduction techniques designed for relational data, have proven useful in exploring and modeling network structure. Most dimensionality reduction methods allow out-of-sample extensions, by which an embedding can be applied to observations not present in the training set. Applied to graphs, the out-of-sample extension problem concerns how to compute the embedding of a vertex that is added to the graph after an embedding has already been computed. In this paper, we consider the out-of-sample extension problem for two graph embedding procedures: the adjacency spectral embedding and the Laplacian spectral embedding. In both cases, we prove that when the underlying graph is generated according to a latent space model called the random dot product graph, which includes the popular stochastic block model as a special case, an out-of-sample extension based on a least-squares objective obeys a central limit theorem about the true latent position of the out-of-sample vertex. In addition, we prove a concentration inequality for the out-of-sample extension of the adjacency spectral embedding based on a maximum-likelihood objective. Our results also yield a convenient framework in which to analyze trade-offs between estimation accuracy and computational expense, which we explore briefly.
Recovering low-rank structure from multiple networks with unknown edge distributions
Jun 13, 2019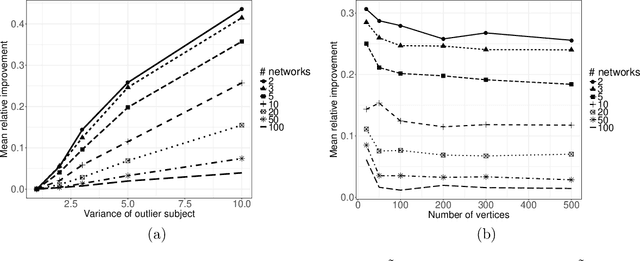
Abstract:In increasingly many settings, particularly in neuroimaging, data sets consist of multiple samples from a population of networks, with vertices aligned across networks. For example, fMRI studies yield graphs whose vertices correspond to brain regions, which are the same across subjects. We consider the setting where we observe a sample of networks whose adjacency matrices have a shared low-rank expectation, but edge-level noise distributions may vary from one network to another. We show that so long as edge noise is sub-gamma distributed in each network, the shared low-rank structure can be recovered accurately using an eigenvalue truncation of a weighted network average. We also explore the extent to which edge-level errors influence estimation and downstream inference tasks. The proposed approach is illustrated on synthetic networks and on an fMRI study of schizophrenia.
On consistent vertex nomination schemes
May 29, 2018
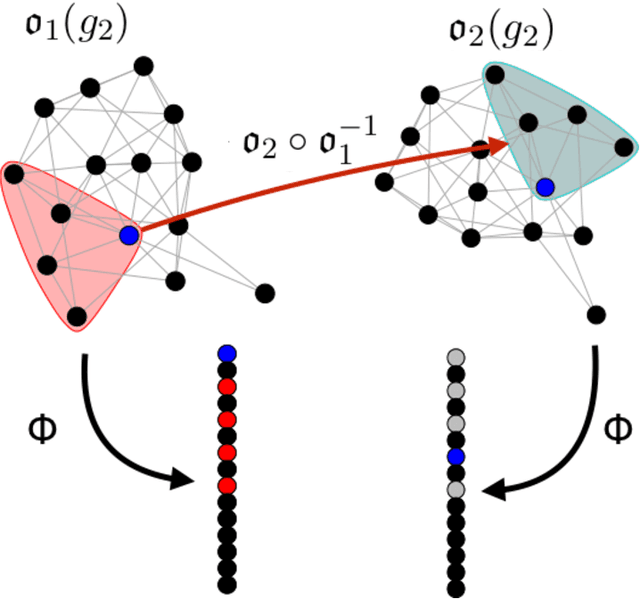
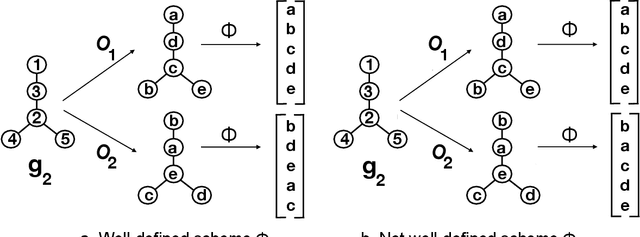
Abstract:Given a vertex of interest in a network $G_1$, the vertex nomination problem seeks to find the corresponding vertex of interest (if it exists) in a second network $G_2$. A vertex nomination scheme produces a rank list of the vertices in $G_2$, where the vertices are ranked by how likely they are judged to be the corresponding vertex of interest in $G_2$. The vertex nomination problem and related information retrieval tasks have attracted much attention in the machine learning literature, with numerous applications in social and biological networks. However, the current framework has often been confined to a comparatively small class of network models, and the concept of statistically consistent vertex nomination schemes has been only shallowly explored. In this paper, we extend the vertex nomination problem to a very general statistical model of graphs. Further, drawing inspiration from the long-established classification framework in the pattern recognition literature, we provide definitions for the key notions of Bayes optimality and consistency in our extended vertex nomination framework, including a derivation of the Bayes optimal vertex nomination scheme. In addition, we prove that no universally consistent vertex nomination schemes exist. Illustrative examples are provided throughout.
Out-of-sample extension of graph adjacency spectral embedding
Feb 17, 2018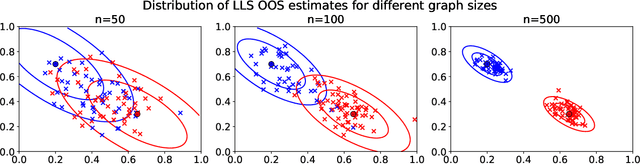
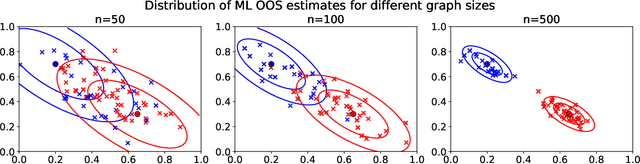
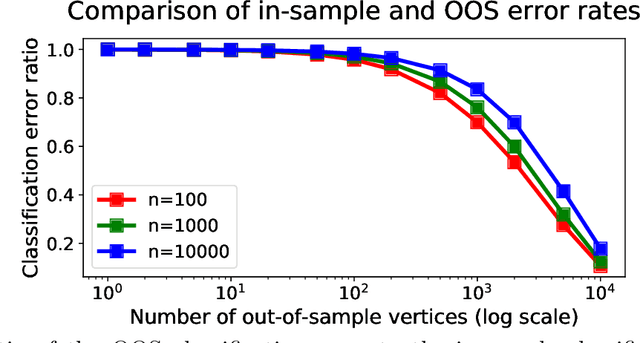
Abstract:Many popular dimensionality reduction procedures have out-of-sample extensions, which allow a practitioner to apply a learned embedding to observations not seen in the initial training sample. In this work, we consider the problem of obtaining an out-of-sample extension for the adjacency spectral embedding, a procedure for embedding the vertices of a graph into Euclidean space. We present two different approaches to this problem, one based on a least-squares objective and the other based on a maximum-likelihood formulation. We show that if the graph of interest is drawn according to a certain latent position model called a random dot product graph, then both of these out-of-sample extensions estimate the true latent position of the out-of-sample vertex with the same error rate. Further, we prove a central limit theorem for the least-squares-based extension, showing that the estimate is asymptotically normal about the truth in the large-graph limit.
Vertex nomination: The canonical sampling and the extended spectral nomination schemes
Feb 14, 2018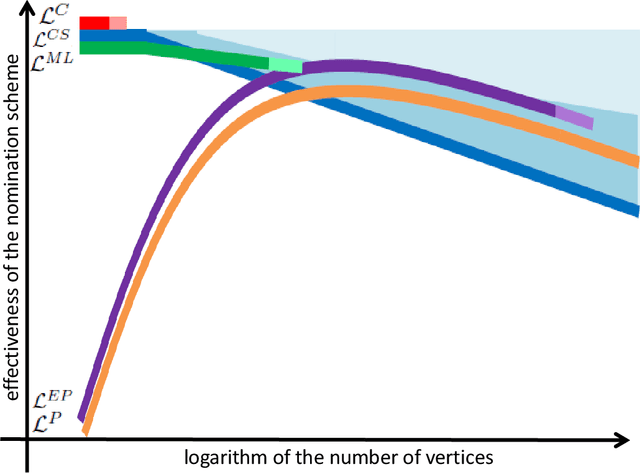
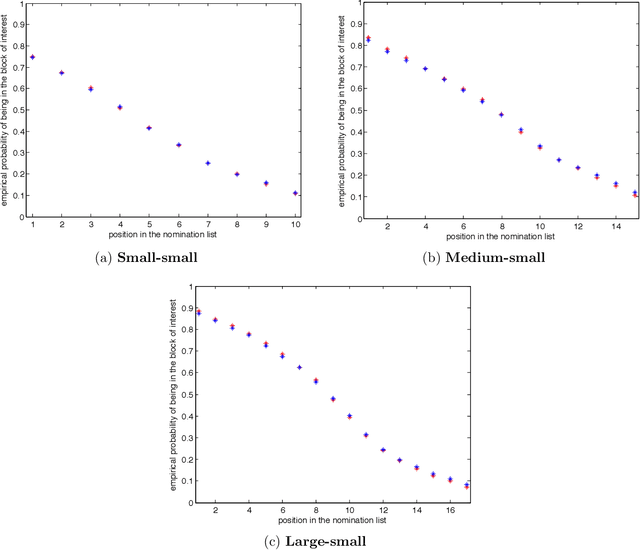
Abstract:Suppose that one particular block in a stochastic block model is deemed "interesting," but block labels are only observed for a few of the vertices. Utilizing a graph realized from the model, the vertex nomination task is to order the vertices with unobserved block labels into a "nomination list" with the goal of having an abundance of interesting vertices near the top of the list. In this paper we extend and enhance two basic vertex nomination schemes; the canonical nomination scheme ${\mathcal L}^C$ and the spectral partitioning nomination scheme ${\mathcal L}^P$. The canonical nomination scheme ${\mathcal L}^C$ is provably optimal, but is computationally intractable, being impractical to implement even on modestly sized graphs. With this in mind, we introduce a scalable, Markov chain Monte Carlo-based nomination scheme, called the {\it canonical sampling nomination scheme} ${\mathcal L}^{CS}$, that converges to the canonical nomination scheme ${\mathcal L}^{C}$ as the amount of sampling goes to infinity. We also introduce a novel spectral partitioning nomination scheme called the {\it extended spectral partitioning nomination scheme} ${\mathcal L}^{EP}$. Real-data and simulation experiments are employed to illustrate the effectiveness of these vertex nomination schemes, as well as their empirical computational complexity.
Statistical inference on random dot product graphs: a survey
Sep 16, 2017

Abstract:The random dot product graph (RDPG) is an independent-edge random graph that is analytically tractable and, simultaneously, either encompasses or can successfully approximate a wide range of random graphs, from relatively simple stochastic block models to complex latent position graphs. In this survey paper, we describe a comprehensive paradigm for statistical inference on random dot product graphs, a paradigm centered on spectral embeddings of adjacency and Laplacian matrices. We examine the analogues, in graph inference, of several canonical tenets of classical Euclidean inference: in particular, we summarize a body of existing results on the consistency and asymptotic normality of the adjacency and Laplacian spectral embeddings, and the role these spectral embeddings can play in the construction of single- and multi-sample hypothesis tests for graph data. We investigate several real-world applications, including community detection and classification in large social networks and the determination of functional and biologically relevant network properties from an exploratory data analysis of the Drosophila connectome. We outline requisite background and current open problems in spectral graph inference.
* An expository survey paper on a comprehensive paradigm for inference for random dot product graphs, centered on graph adjacency and Laplacian spectral embeddings. Paper outlines requisite background; summarizes theory, methodology, and applications from previous and ongoing work; and closes with a discussion of several open problems
Query-by-Example Search with Discriminative Neural Acoustic Word Embeddings
Jun 12, 2017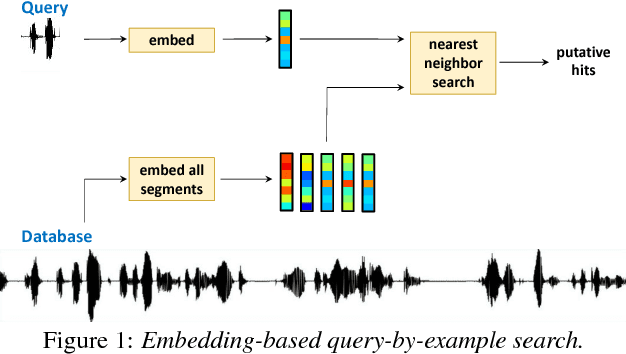
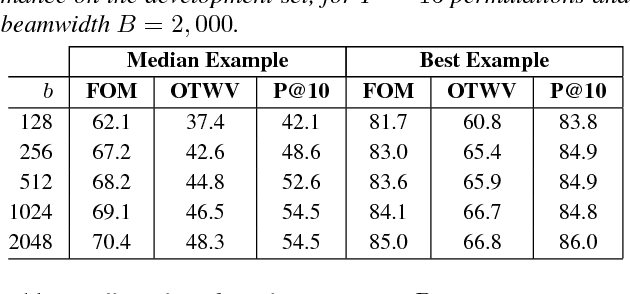
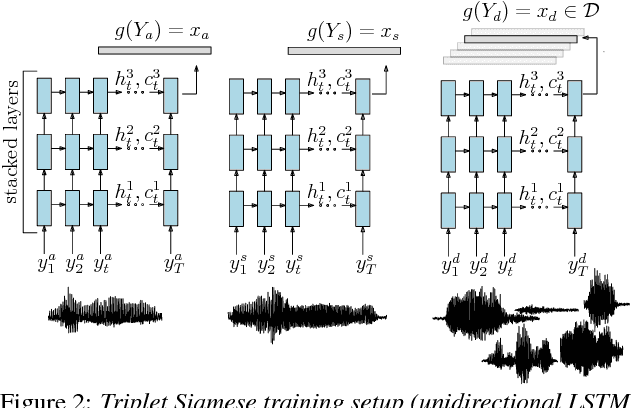

Abstract:Query-by-example search often uses dynamic time warping (DTW) for comparing queries and proposed matching segments. Recent work has shown that comparing speech segments by representing them as fixed-dimensional vectors --- acoustic word embeddings --- and measuring their vector distance (e.g., cosine distance) can discriminate between words more accurately than DTW-based approaches. We consider an approach to query-by-example search that embeds both the query and database segments according to a neural model, followed by nearest-neighbor search to find the matching segments. Earlier work on embedding-based query-by-example, using template-based acoustic word embeddings, achieved competitive performance. We find that our embeddings, based on recurrent neural networks trained to optimize word discrimination, achieve substantial improvements in performance and run-time efficiency over the previous approaches.
On the Consistency of the Likelihood Maximization Vertex Nomination Scheme: Bridging the Gap Between Maximum Likelihood Estimation and Graph Matching
Aug 27, 2016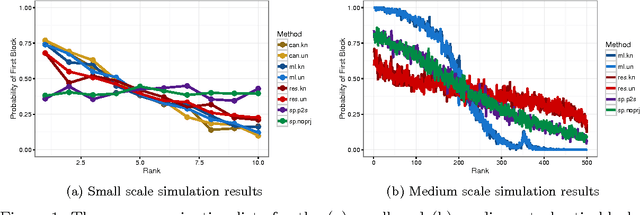



Abstract:Given a graph in which a few vertices are deemed interesting a priori, the vertex nomination task is to order the remaining vertices into a nomination list such that there is a concentration of interesting vertices at the top of the list. Previous work has yielded several approaches to this problem, with theoretical results in the setting where the graph is drawn from a stochastic block model (SBM), including a vertex nomination analogue of the Bayes optimal classifier. In this paper, we prove that maximum likelihood (ML)-based vertex nomination is consistent, in the sense that the performance of the ML-based scheme asymptotically matches that of the Bayes optimal scheme. We prove theorems of this form both when model parameters are known and unknown. Additionally, we introduce and prove consistency of a related, more scalable restricted-focus ML vertex nomination scheme. Finally, we incorporate vertex and edge features into ML-based vertex nomination and briefly explore the empirical effectiveness of this approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge