Optimizing the Induced Correlation in Omnibus Joint Graph Embeddings

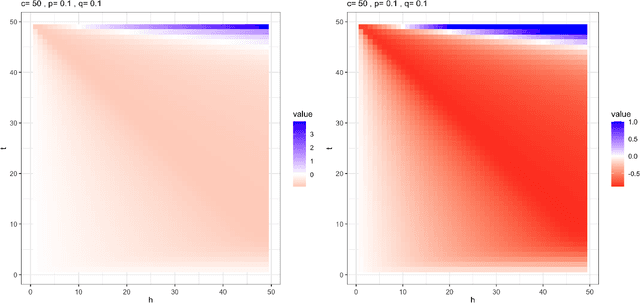
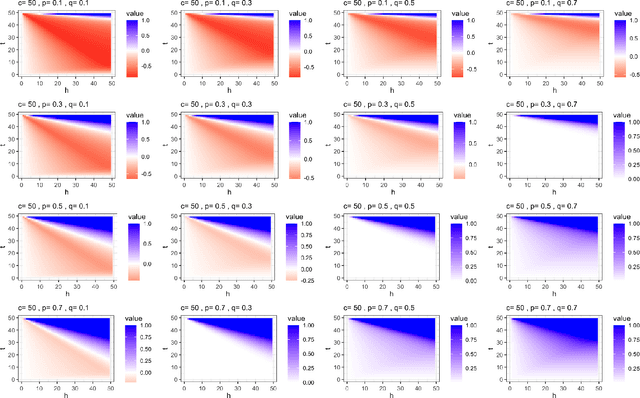
Theoretical and empirical evidence suggests that joint graph embedding algorithms induce correlation across the networks in the embedding space. In the Omnibus joint graph embedding framework, previous results explicitly delineated the dual effects of the algorithm-induced and model-inherent correlations on the correlation across the embedded networks. Accounting for and mitigating the algorithm-induced correlation is key to subsequent inference, as sub-optimal Omnibus matrix constructions have been demonstrated to lead to loss in inference fidelity. This work presents the first efforts to automate the Omnibus construction in order to address two key questions in this joint embedding framework: the correlation-to-OMNI problem and the flat correlation problem. In the flat correlation problem, we seek to understand the minimum algorithm-induced flat correlation (i.e., the same across all graph pairs) produced by a generalized Omnibus embedding. Working in a subspace of the fully general Omnibus matrices, we prove both a lower bound for this flat correlation and that the classical Omnibus construction induces the maximal flat correlation. In the correlation-to-OMNI problem, we present an algorithm -- named corr2Omni -- that, from a given matrix of estimated pairwise graph correlations, estimates the matrix of generalized Omnibus weights that induces optimal correlation in the embedding space. Moreover, in both simulated and real data settings, we demonstrate the increased effectiveness of our corr2Omni algorithm versus the classical Omnibus construction.

Detection of Model-based Planted Pseudo-cliques in Random Dot Product Graphs by the Adjacency Spectral Embedding and the Graph Encoder Embedding

In this paper, we explore the capability of both the Adjacency Spectral Embedding (ASE) and the Graph Encoder Embedding (GEE) for capturing an embedded pseudo-clique structure in the random dot product graph setting. In both theory and experiments, we demonstrate that this pairing of model and methods can yield worse results than the best existing spectral clique detection methods, demonstrating at once the methods' potential inability to capture even modestly sized pseudo-cliques and the methods' robustness to the model contamination giving rise to the pseudo-clique structure. To further enrich our analysis, we also consider the Variational Graph Auto-Encoder (VGAE) model in our simulation and real data experiments.

Gotta match 'em all: Solution diversification in graph matching matched filters

We present a novel approach for finding multiple noisily embedded template graphs in a very large background graph. Our method builds upon the graph-matching-matched-filter technique proposed in Sussman et al., with the discovery of multiple diverse matchings being achieved by iteratively penalizing a suitable node-pair similarity matrix in the matched filter algorithm. In addition, we propose algorithmic speed-ups that greatly enhance the scalability of our matched-filter approach. We present theoretical justification of our methodology in the setting of correlated Erdos-Renyi graphs, showing its ability to sequentially discover multiple templates under mild model conditions. We additionally demonstrate our method's utility via extensive experiments both using simulated models and real-world dataset, include human brain connectomes and a large transactional knowledge base.

Lost in the Shuffle: Testing Power in the Presence of Errorful Network Vertex Labels

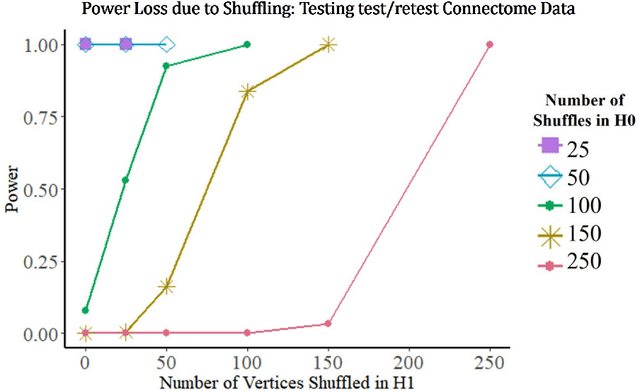
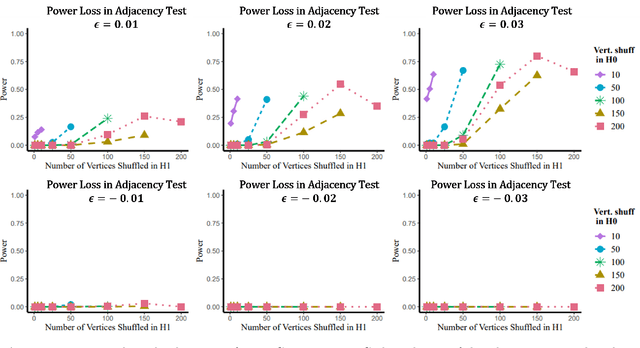
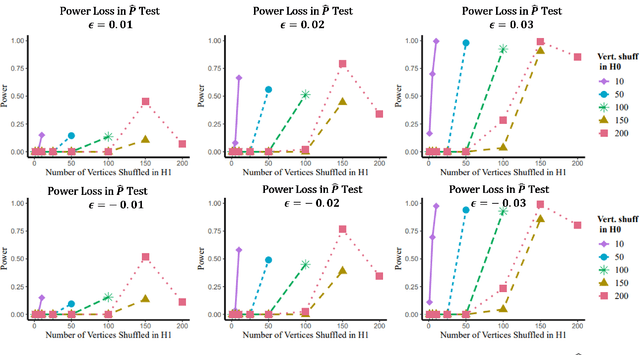
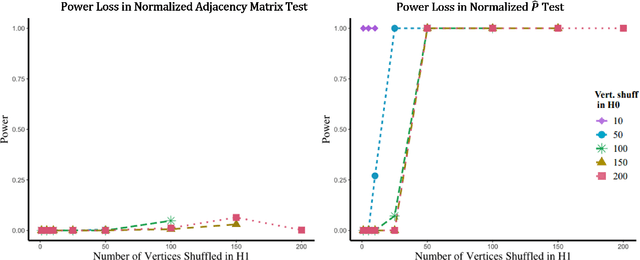
Many two-sample network hypothesis testing methodologies operate under the implicit assumption that the vertex correspondence across networks is a priori known. In this paper, we consider the degradation of power in two-sample graph hypothesis testing when there are misaligned/label-shuffled vertices across networks. In the context of stochastic block model networks, we theoretically explore the power loss due to shuffling for a pair of hypothesis tests based on Frobenius norm differences between estimated edge probability matrices or between adjacency matrices. The loss in testing power is further reinforced by numerous simulations and experiments, both in the stochastic block model and in the random dot product graph model, where we compare the power loss across multiple recently proposed tests in the literature. Lastly, we demonstrate the impact that shuffling can have in real-data testing in a pair of examples from neuroscience and from social network analysis.

Adversarial contamination of networks in the setting of vertex nomination: a new trimming method

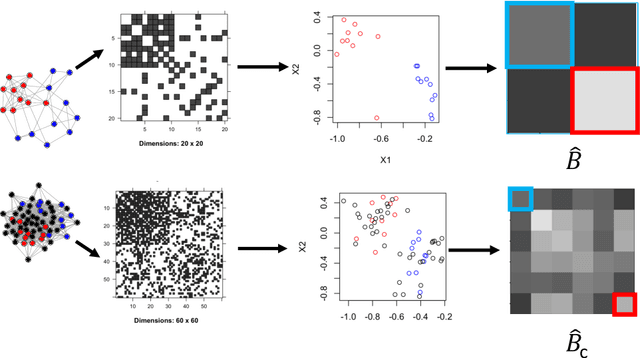
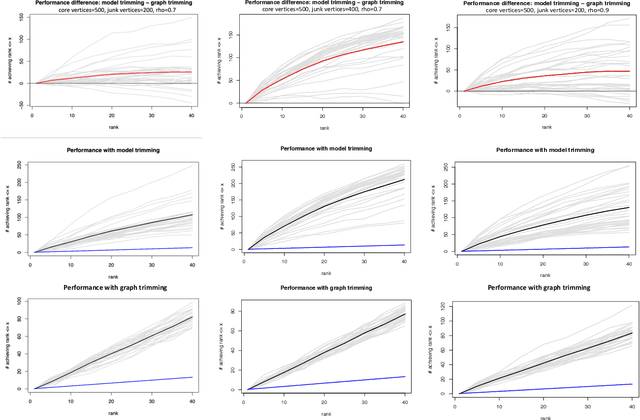
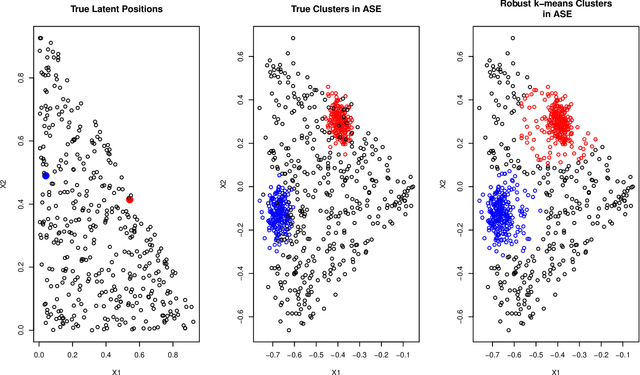
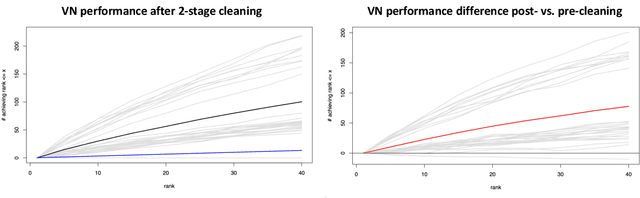
As graph data becomes more ubiquitous, the need for robust inferential graph algorithms to operate in these complex data domains is crucial. In many cases of interest, inference is further complicated by the presence of adversarial data contamination. The effect of the adversary is frequently to change the data distribution in ways that negatively affect statistical and algorithmic performance. We study this phenomenon in the context of vertex nomination, a semi-supervised information retrieval task for network data. Here, a common suite of methods relies on spectral graph embeddings, which have been shown to provide both good algorithmic performance and flexible settings in which regularization techniques can be implemented to help mitigate the effect of an adversary. Many current regularization methods rely on direct network trimming to effectively excise the adversarial contamination, although this direct trimming often gives rise to complicated dependency structures in the resulting graph. We propose a new trimming method that operates in model space which can address both block structure contamination and white noise contamination (contamination whose distribution is unknown). This model trimming is more amenable to theoretical analysis while also demonstrating superior performance in a number of simulations, compared to direct trimming.

Clustered Graph Matching for Label Recovery and Graph Classification

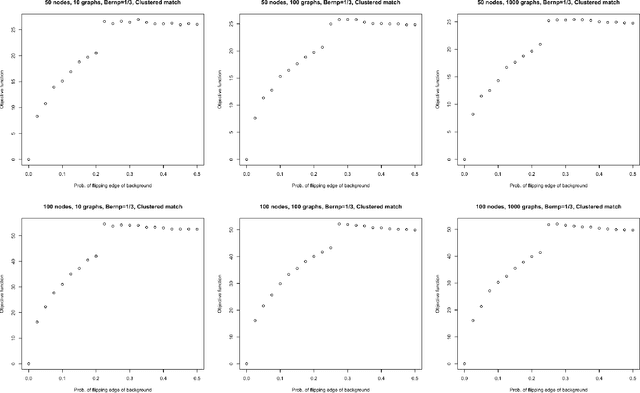
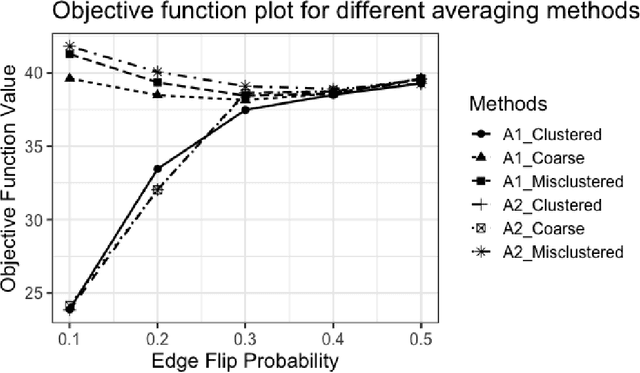
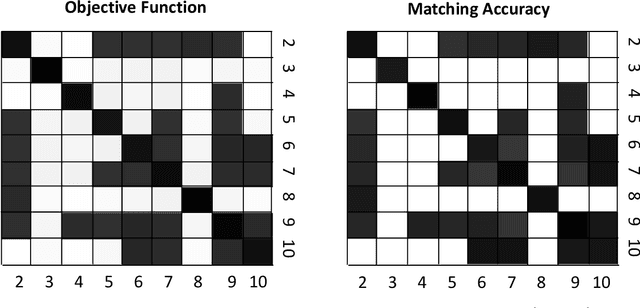
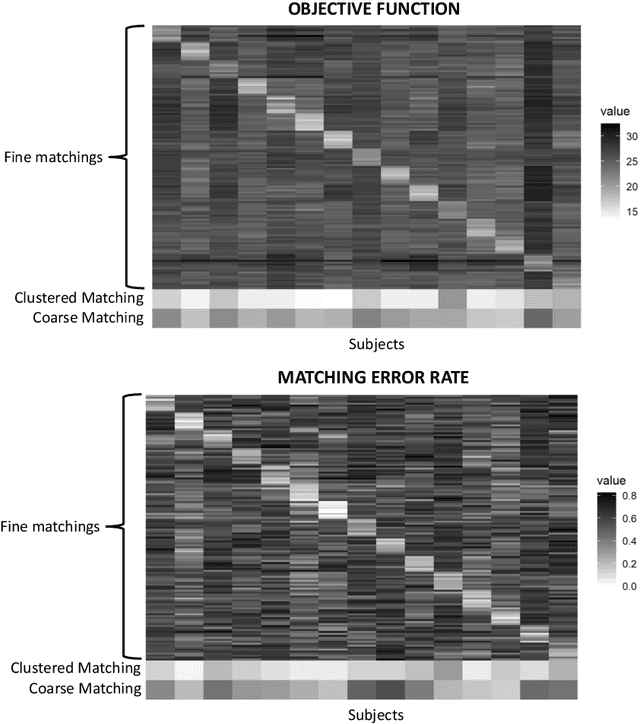
Given a collection of vertex-aligned networks and an additional label-shuffled network, we propose procedures for leveraging the signal in the vertex-aligned collection to recover the labels of the shuffled network. We consider matching the shuffled network to averages of the networks in the vertex-aligned collection at different levels of granularity. We demonstrate both in theory and practice that if the graphs come from different network classes, then clustering the networks into classes followed by matching the new graph to cluster-averages can yield higher fidelity matching performance than matching to the global average graph. Moreover, by minimizing the graph matching objective function with respect to each cluster average, this approach simultaneously classifies and recovers the vertex labels for the shuffled graph.

Leveraging semantically similar queries for ranking via combining representations

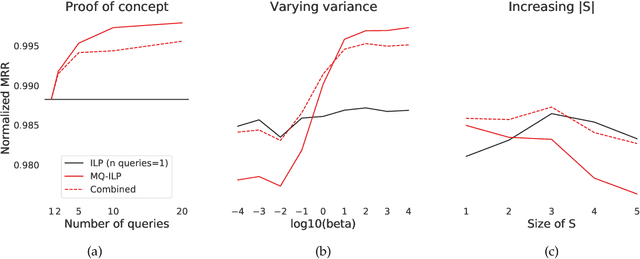
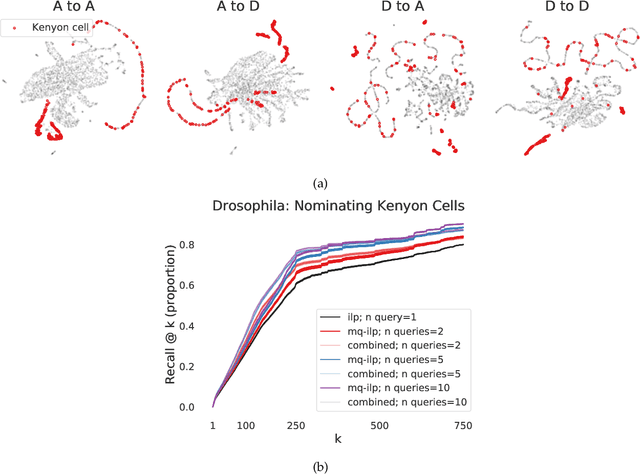
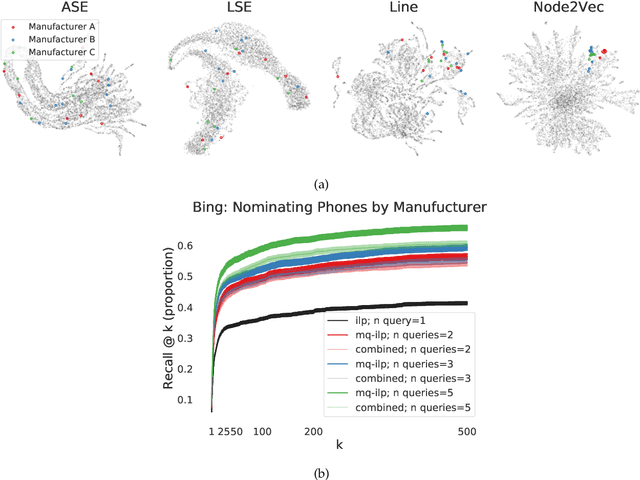
In modern ranking problems, different and disparate representations of the items to be ranked are often available. It is sensible, then, to try to combine these representations to improve ranking. Indeed, learning to rank via combining representations is both principled and practical for learning a ranking function for a particular query. In extremely data-scarce settings, however, the amount of labeled data available for a particular query can lead to a highly variable and ineffective ranking function. One way to mitigate the effect of the small amount of data is to leverage information from semantically similar queries. Indeed, as we demonstrate in simulation settings and real data examples, when semantically similar queries are available it is possible to gainfully use them when ranking with respect to a particular query. We describe and explore this phenomenon in the context of the bias-variance trade off and apply it to the data-scarce settings of a Bing navigational graph and the Drosophila larva connectome.

Subgraph nomination: Query by Example Subgraph Retrieval in Networks

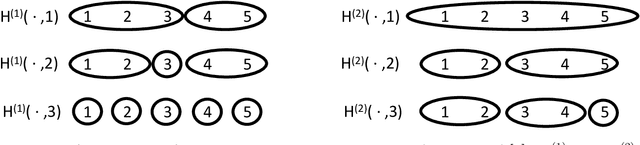
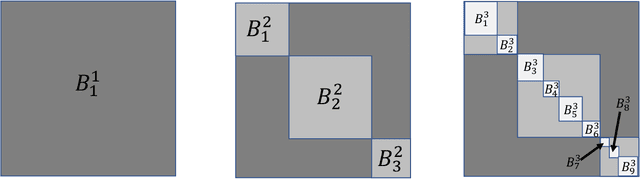
This paper introduces the subgraph nomination inference task, in which example subgraphs of interest are used to query a network for similarly interesting subgraphs. This type of problem appears time and again in real world problems connected to, for example, user recommendation systems and structural retrieval tasks in social and biological/connectomic networks. We formally define the subgraph nomination framework with an emphasis on the notion of a user-in-the-loop in the subgraph nomination pipeline. In this setting, a user can provide additional post-nomination light supervision that can be incorporated into the retrieval task. After introducing and formalizing the retrieval task, we examine the nuanced effect that user-supervision can have on performance, both analytically and across real and simulated data examples.

The Importance of Being Correlated: Implications of Dependence in Joint Spectral Inference across Multiple Networks

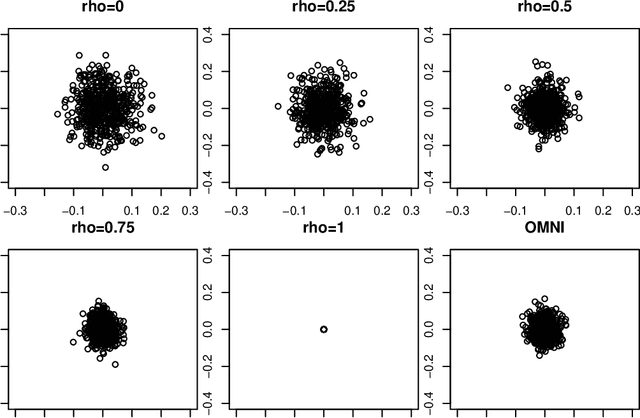
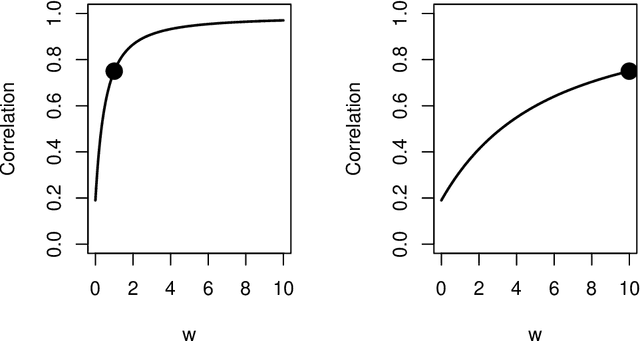
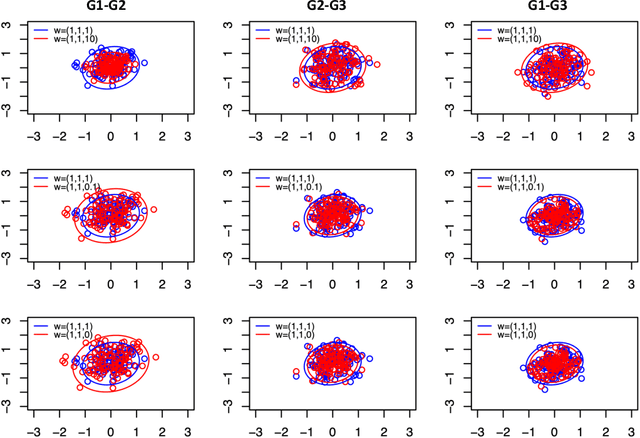
Spectral inference on multiple networks is a rapidly-developing subfield of graph statistics. Recent work has demonstrated that joint, or simultaneous, spectral embedding of multiple independent network realizations can deliver more accurate estimation than individual spectral decompositions of those same networks. Little attention has been paid, however, to the network correlation that such joint embedding procedures necessarily induce. In this paper, we present a detailed analysis of induced correlation in a {\em generalized omnibus} embedding for multiple networks. We show that our embedding procedure is flexible and robust, and, moreover, we prove a central limit theorem for this embedding and explicitly compute the limiting covariance. We examine how this covariance can impact inference in a network time series, and we construct an appropriately calibrated omnibus embedding that can detect changes in real biological networks that previous embedding procedures could not discern. Our analysis confirms that the effect of induced correlation can be both subtle and transformative, with import in theory and practice.

On the role of features in vertex nomination: Content and context together are better

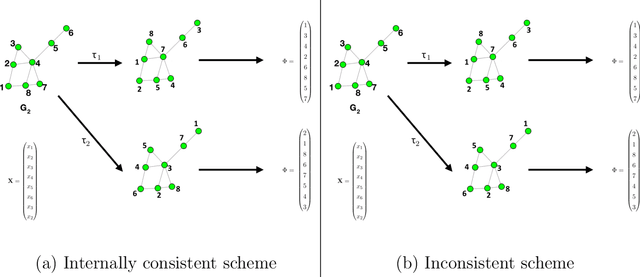
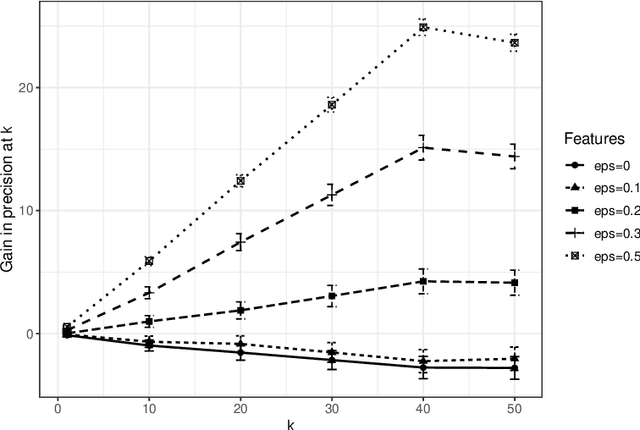
Vertex nomination is a lightly-supervised network information retrieval (IR) task in which vertices of interest in one graph are used to query a second graph to discover vertices of interest in the second graph. Similar to other IR tasks, the output of a vertex nomination scheme is a ranked list of the vertices in the second graph, with the heretofore unknown vertices of interest ideally concentrating at the top of the list. Vertex nomination schemes provide a useful suite of tools for efficiently mining complex networks for pertinent information. In this paper, we explore, both theoretically and practically, the dual roles of content (i.e., edge and vertex attributes) and context (i.e., network topology) in vertex nomination. We provide necessary and sufficient conditions under which vertex nomination schemes that leverage both content and context outperform schemes that leverage only content or context separately. While the joint utility of both content and context has been demonstrated empirically in the literature, the framework presented in this paper provides a novel theoretical basis for understanding the potential complementary roles of network features and topology.