Gotta match 'em all: Solution diversification in graph matching matched filters

We present a novel approach for finding multiple noisily embedded template graphs in a very large background graph. Our method builds upon the graph-matching-matched-filter technique proposed in Sussman et al., with the discovery of multiple diverse matchings being achieved by iteratively penalizing a suitable node-pair similarity matrix in the matched filter algorithm. In addition, we propose algorithmic speed-ups that greatly enhance the scalability of our matched-filter approach. We present theoretical justification of our methodology in the setting of correlated Erdos-Renyi graphs, showing its ability to sequentially discover multiple templates under mild model conditions. We additionally demonstrate our method's utility via extensive experiments both using simulated models and real-world dataset, include human brain connectomes and a large transactional knowledge base.

Maximum Likelihood Estimation and Graph Matching in Errorfully Observed Networks

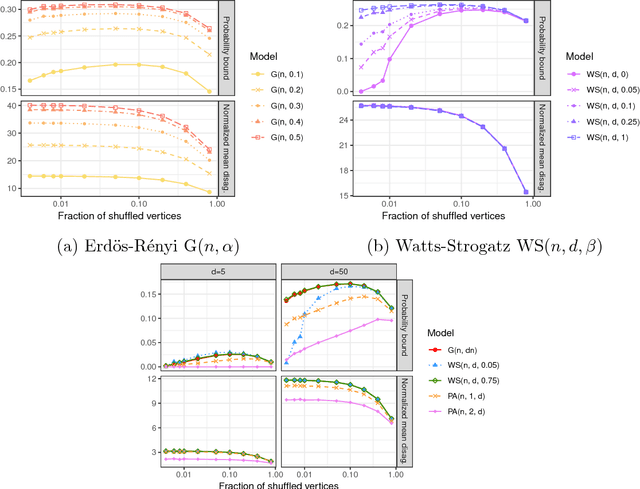
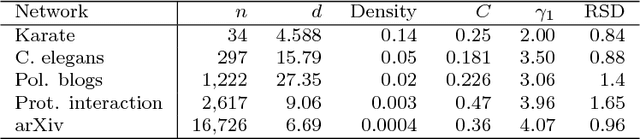
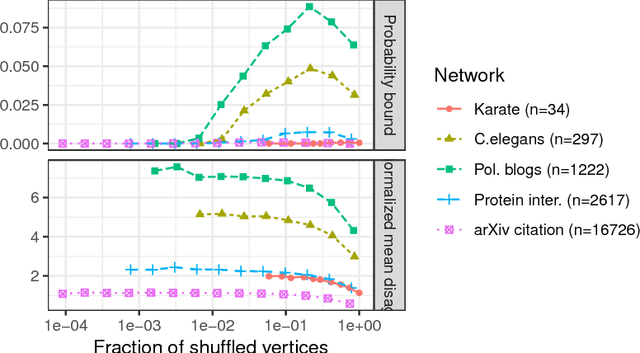
Given a pair of graphs with the same number of vertices, the inexact graph matching problem consists in finding a correspondence between the vertices of these graphs that minimizes the total number of induced edge disagreements. We study this problem from a statistical framework in which one of the graphs is an errorfully observed copy of the other. We introduce a corrupting channel model, and show that in this model framework, the solution to the graph matching problem is a maximum likelihood estimator. Necessary and sufficient conditions for consistency of this MLE are presented, as well as a relaxed notion of consistency in which a negligible fraction of the vertices need not be matched correctly. The results are used to study matchability in several families of random graphs, including edge independent models, random regular graphs and small-world networks. We also use these results to introduce measures of matching feasibility, and experimentally validate the results on simulated and real-world networks.

Matched Filters for Noisy Induced Subgraph Detection

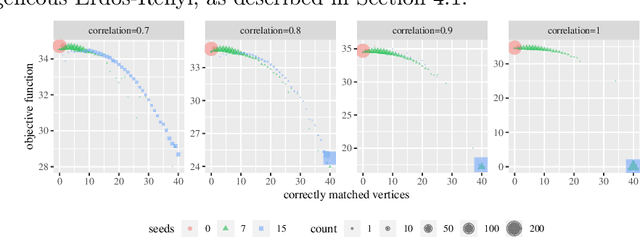
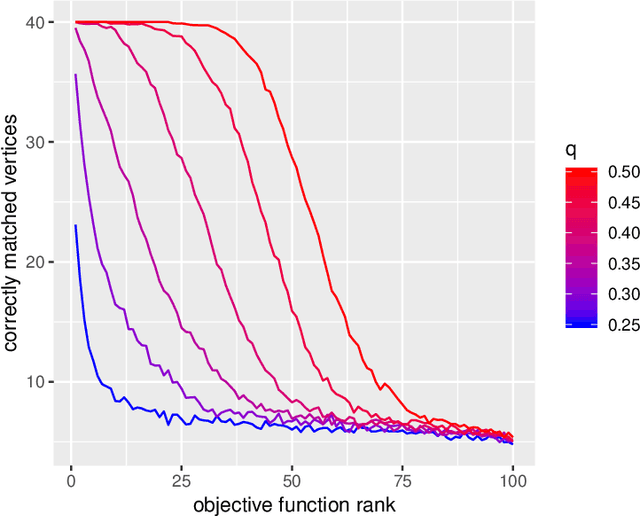
We consider the problem of finding the vertex correspondence between two graphs with different number of vertices where the smaller graph is still potentially large. We propose a solution to this problem via a graph matching matched filter: padding the smaller graph in different ways and then using graph matching methods to align it to the larger network. Under a statistical model for correlated pairs of graphs, which yields a noisy copy of the small graph within the larger graph, the resulting optimization problem can be guaranteed to recover the true vertex correspondence between the networks, though there are currently no efficient algorithms for solving this problem. We consider an approach that exploits a partially known correspondence and show via varied simulations and applications to the Drosophila connectome that in practice this approach can achieve good performance.

Connectome Smoothing via Low-rank Approximations

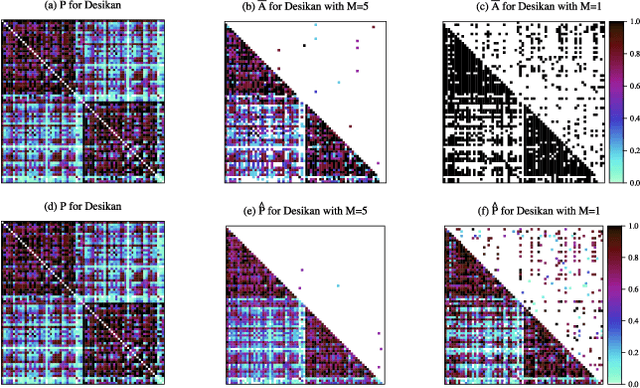
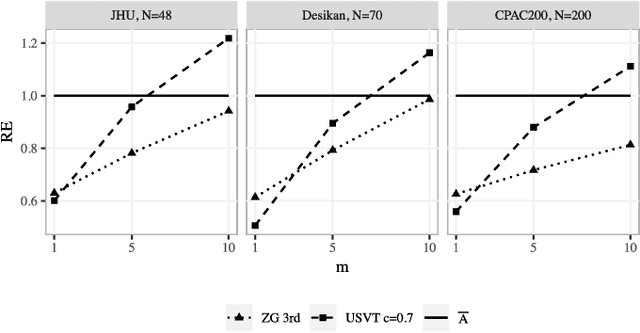
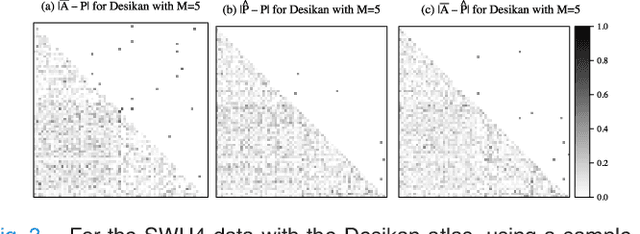
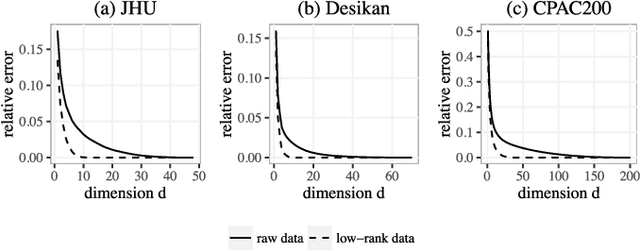
In statistical connectomics, the quantitative study of brain networks, estimating the mean of a population of graphs based on a sample is a core problem. Often, this problem is especially difficult because the sample or cohort size is relatively small, sometimes even a single subject. While using the element-wise sample mean of the adjacency matrices is a common approach, this method does not exploit any underlying structural properties of the graphs. We propose using a low-rank method which incorporates tools for dimension selection and diagonal augmentation to smooth the estimates and improve performance over the naive methodology for small sample sizes. Theoretical results for the stochastic blockmodel show that this method offers major improvements when there are many vertices. Similarly, we demonstrate that the low-rank methods outperform the standard sample mean for a variety of independent edge distributions as well as human connectome data derived from magnetic resonance imaging, especially when sample sizes are small. Moreover, the low-rank methods yield "eigen-connectomes", which correlate with the lobe-structure of the human brain and superstructures of the mouse brain. These results indicate that low-rank methods are an important part of the tool box for researchers studying populations of graphs in general, and statistical connectomics in particular.

Statistical inference on random dot product graphs: a survey

The random dot product graph (RDPG) is an independent-edge random graph that is analytically tractable and, simultaneously, either encompasses or can successfully approximate a wide range of random graphs, from relatively simple stochastic block models to complex latent position graphs. In this survey paper, we describe a comprehensive paradigm for statistical inference on random dot product graphs, a paradigm centered on spectral embeddings of adjacency and Laplacian matrices. We examine the analogues, in graph inference, of several canonical tenets of classical Euclidean inference: in particular, we summarize a body of existing results on the consistency and asymptotic normality of the adjacency and Laplacian spectral embeddings, and the role these spectral embeddings can play in the construction of single- and multi-sample hypothesis tests for graph data. We investigate several real-world applications, including community detection and classification in large social networks and the determination of functional and biologically relevant network properties from an exploratory data analysis of the Drosophila connectome. We outline requisite background and current open problems in spectral graph inference.

Empirical Bayes Estimation for the Stochastic Blockmodel

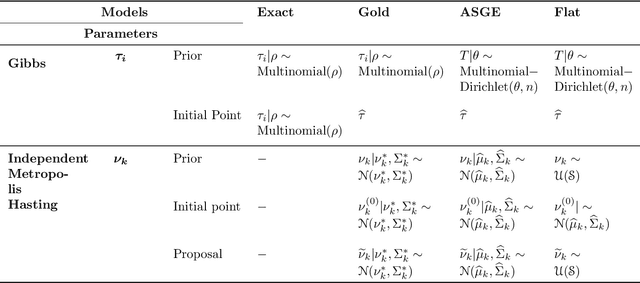
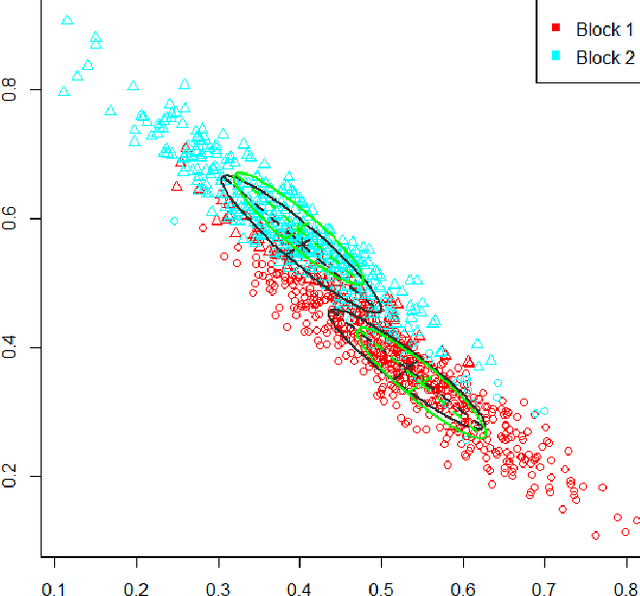
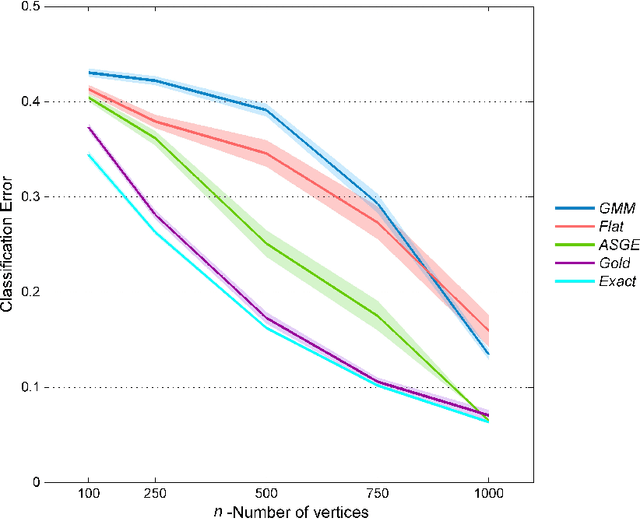
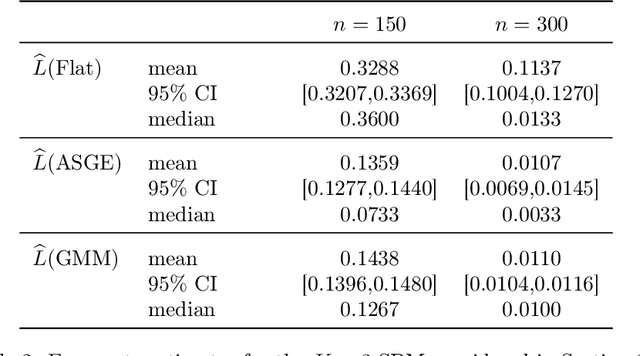
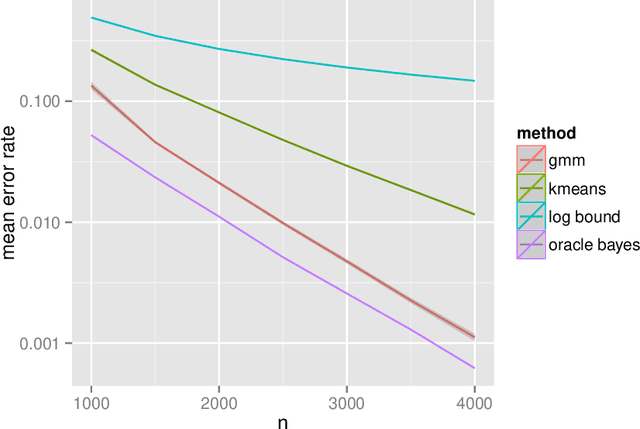
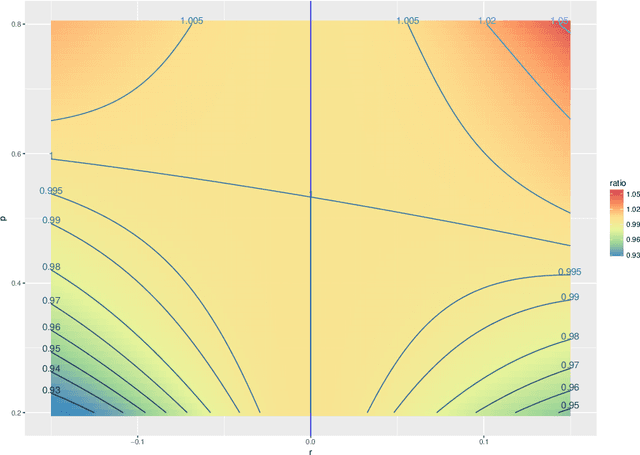
Inference for the stochastic blockmodel is currently of burgeoning interest in the statistical community, as well as in various application domains as diverse as social networks, citation networks, brain connectivity networks (connectomics), etc. Recent theoretical developments have shown that spectral embedding of graphs yields tractable distributional results; in particular, a random dot product latent position graph formulation of the stochastic blockmodel informs a mixture of normal distributions for the adjacency spectral embedding. We employ this new theory to provide an empirical Bayes methodology for estimation of block memberships of vertices in a random graph drawn from the stochastic blockmodel, and demonstrate its practical utility. The posterior inference is conducted using a Metropolis-within-Gibbs algorithm. The theory and methods are illustrated through Monte Carlo simulation studies, both within the stochastic blockmodel and beyond, and experimental results on a Wikipedia data set are presented.

Analyzing statistical and computational tradeoffs of estimation procedures

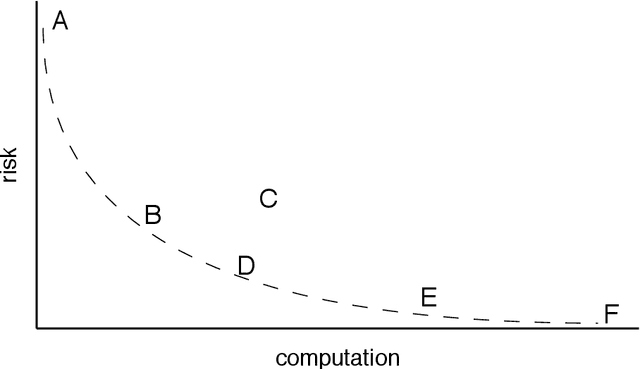
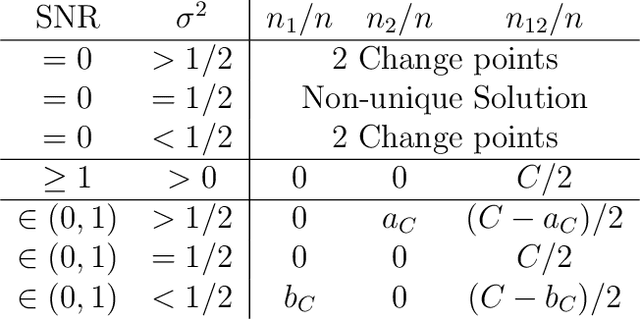
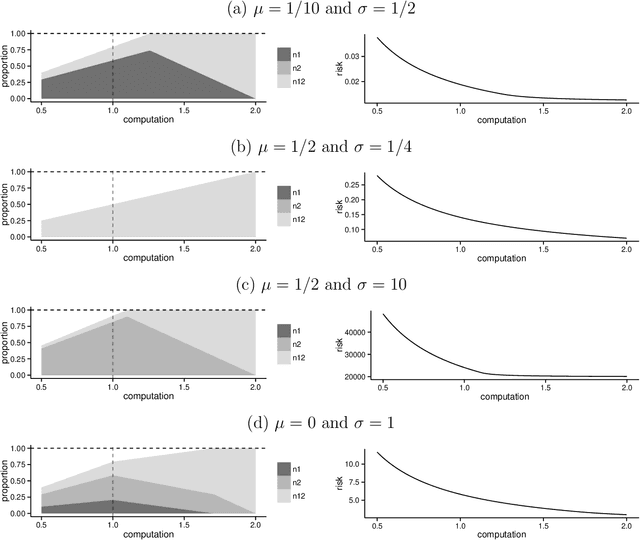
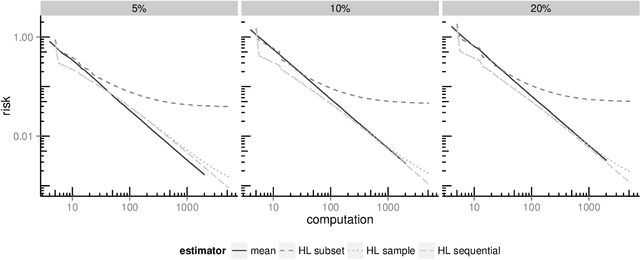
The recent explosion in the amount and dimensionality of data has exacerbated the need of trading off computational and statistical efficiency carefully, so that inference is both tractable and meaningful. We propose a framework that provides an explicit opportunity for practitioners to specify how much statistical risk they are willing to accept for a given computational cost, and leads to a theoretical risk-computation frontier for any given inference problem. We illustrate the tradeoff between risk and computation and illustrate the frontier in three distinct settings. First, we derive analytic forms for the risk of estimating parameters in the classical setting of estimating the mean and variance for normally distributed data and for the more general setting of parameters of an exponential family. The second example concentrates on computationally constrained Hodges-Lehmann estimators. We conclude with an evaluation of risk associated with early termination of iterative matrix inversion algorithms in the context of linear regression.

Spectral Clustering for Divide-and-Conquer Graph Matching

We present a parallelized bijective graph matching algorithm that leverages seeds and is designed to match very large graphs. Our algorithm combines spectral graph embedding with existing state-of-the-art seeded graph matching procedures. We justify our approach by proving that modestly correlated, large stochastic block model random graphs are correctly matched utilizing very few seeds through our divide-and-conquer procedure. We also demonstrate the effectiveness of our approach in matching very large graphs in simulated and real data examples, showing up to a factor of 8 improvement in runtime with minimal sacrifice in accuracy.

Statistical inference on errorfully observed graphs

Statistical inference on graphs is a burgeoning field in the applied and theoretical statistics communities, as well as throughout the wider world of science, engineering, business, etc. In many applications, we are faced with the reality of errorfully observed graphs. That is, the existence of an edge between two vertices is based on some imperfect assessment. In this paper, we consider a graph $G = (V,E)$. We wish to perform an inference task -- the inference task considered here is "vertex classification". However, we do not observe $G$; rather, for each potential edge $uv \in {{V}\choose{2}}$ we observe an "edge-feature" which we use to classify $uv$ as edge/not-edge. Thus we errorfully observe $G$ when we observe the graph $\widetilde{G} = (V,\widetilde{E})$ as the edges in $\widetilde{E}$ arise from the classifications of the "edge-features", and are expected to be errorful. Moreover, we face a quantity/quality trade-off regarding the edge-features we observe -- more informative edge-features are more expensive, and hence the number of potential edges that can be assessed decreases with the quality of the edge-features. We studied this problem by formulating a quantity/quality tradeoff for a simple class of random graphs model, namely the stochastic blockmodel. We then consider a simple but optimal vertex classifier for classifying $v$ and we derive the optimal quantity/quality operating point for subsequent graph inference in the face of this trade-off. The optimal operating points for the quantity/quality trade-off are surprising and illustrate the issue that methods for intermediate tasks should be chosen to maximize performance for the ultimate inference task. Finally, we investigate the quantity/quality tradeoff for errorful obesrvations of the {\it C.\ elegans} connectome graph.

A central limit theorem for scaled eigenvectors of random dot product graphs

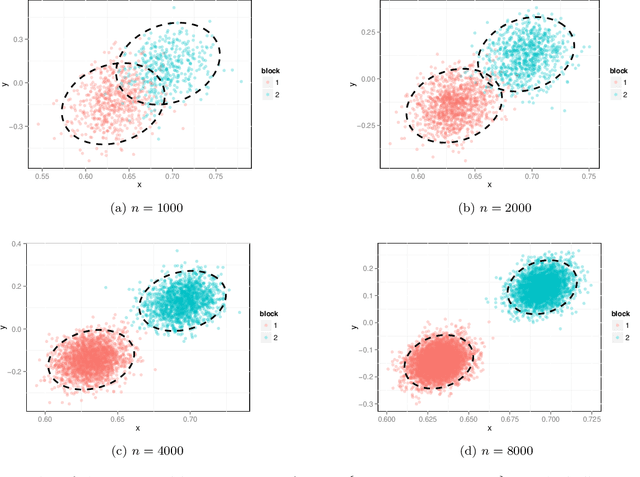
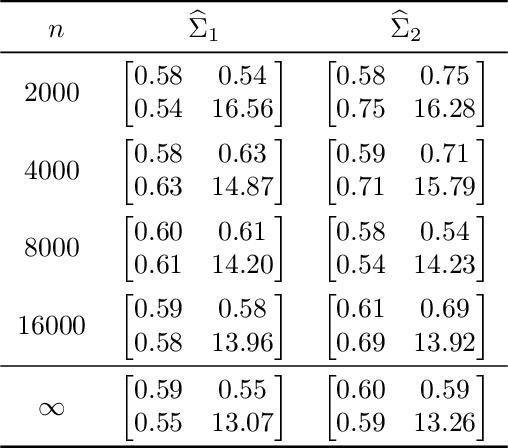
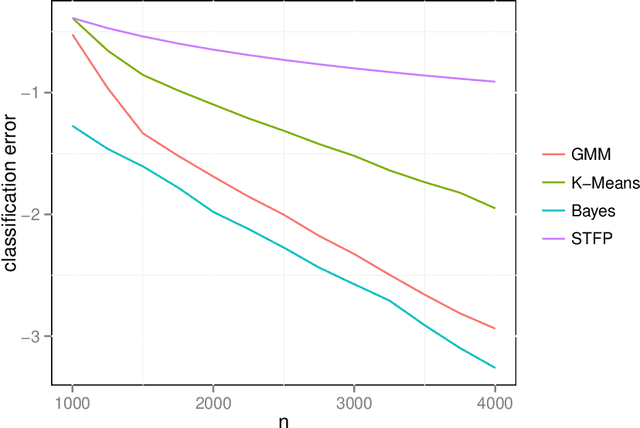
We prove a central limit theorem for the components of the largest eigenvectors of the adjacency matrix of a finite-dimensional random dot product graph whose true latent positions are unknown. In particular, we follow the methodology outlined in \citet{sussman2012universally} to construct consistent estimates for the latent positions, and we show that the appropriately scaled differences between the estimated and true latent positions converge to a mixture of Gaussian random variables. As a corollary, we obtain a central limit theorem for the first eigenvector of the adjacency matrix of an Erd\"os-Renyi random graph.