The Importance of Being Correlated: Implications of Dependence in Joint Spectral Inference across Multiple Networks

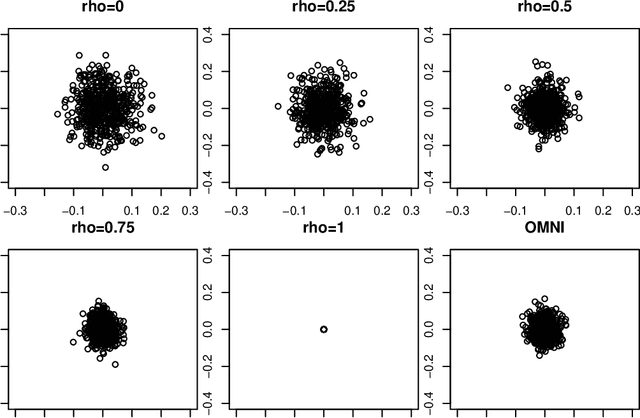
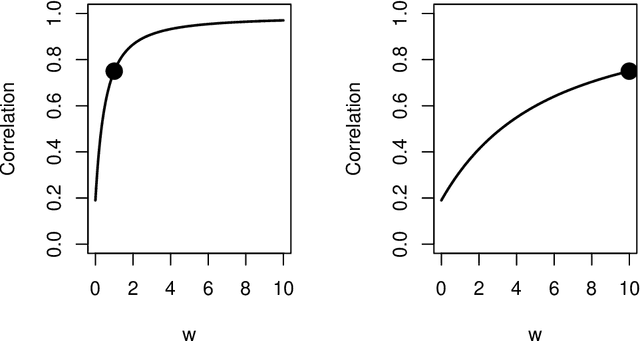
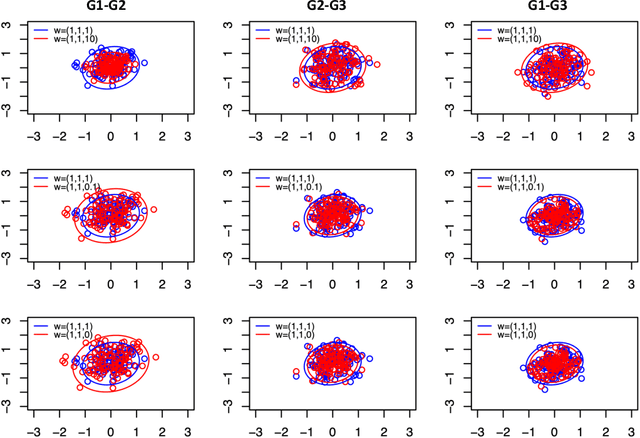
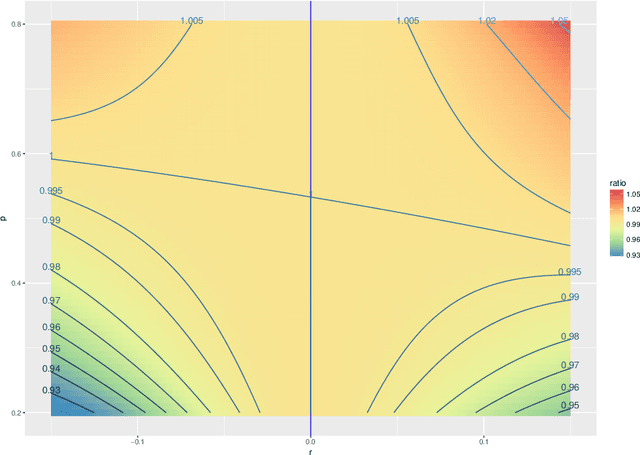
Spectral inference on multiple networks is a rapidly-developing subfield of graph statistics. Recent work has demonstrated that joint, or simultaneous, spectral embedding of multiple independent network realizations can deliver more accurate estimation than individual spectral decompositions of those same networks. Little attention has been paid, however, to the network correlation that such joint embedding procedures necessarily induce. In this paper, we present a detailed analysis of induced correlation in a {\em generalized omnibus} embedding for multiple networks. We show that our embedding procedure is flexible and robust, and, moreover, we prove a central limit theorem for this embedding and explicitly compute the limiting covariance. We examine how this covariance can impact inference in a network time series, and we construct an appropriately calibrated omnibus embedding that can detect changes in real biological networks that previous embedding procedures could not discern. Our analysis confirms that the effect of induced correlation can be both subtle and transformative, with import in theory and practice.

On identifying unobserved heterogeneity in stochastic blockmodel graphs with vertex covariates

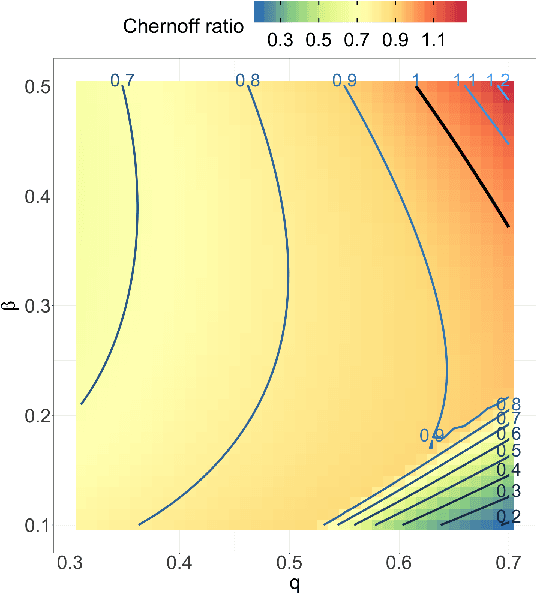
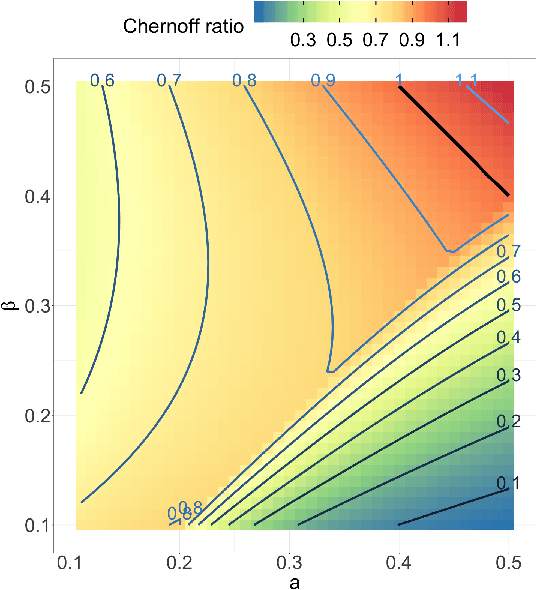
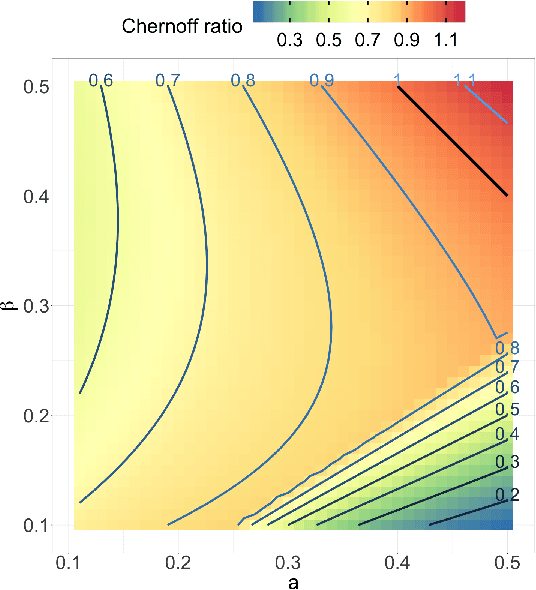
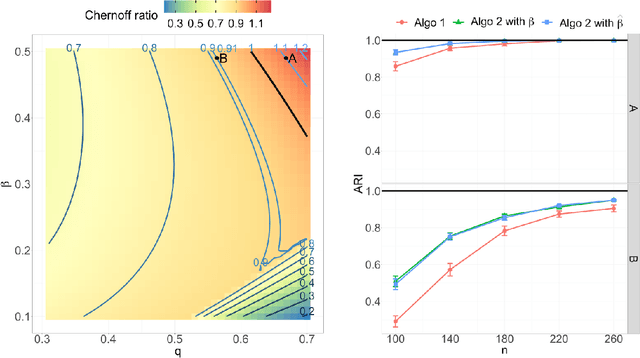
Both observed and unobserved vertex heterogeneity can influence block structure in graphs. To assess these effects on block recovery, we present a comparative analysis of two model-based spectral algorithms for clustering vertices in stochastic blockmodel graphs with vertex covariates. The first algorithm directly estimates the induced block assignments by investigating the estimated block connectivity probability matrix including the vertex covariate effect. The second algorithm estimates the vertex covariate effect and then estimates the induced block assignments after accounting for this effect. We employ Chernoff information to analytically compare the algorithms' performance and derive the Chernoff ratio formula for some special models of interest. Analytic results and simulations suggest that, in general, the second algorithm is preferred: we can better estimate the induced block assignments by first estimating the vertex covariate effect. In addition, real data experiments on a diffusion MRI connectome data set indicate that the second algorithm has the advantages of revealing underlying block structure and taking observed vertex heterogeneity into account in real applications. Our findings emphasize the importance of distinguishing between observed and unobserved factors that can affect block structure in graphs.

Learning to rank via combining representations

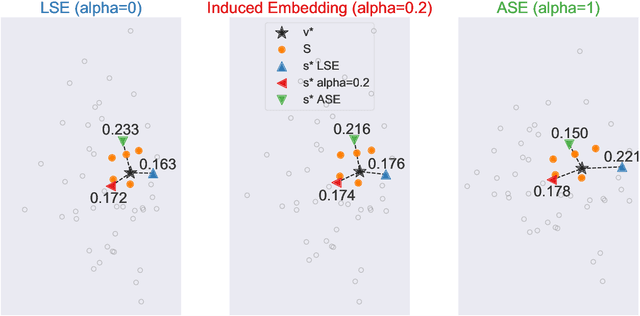
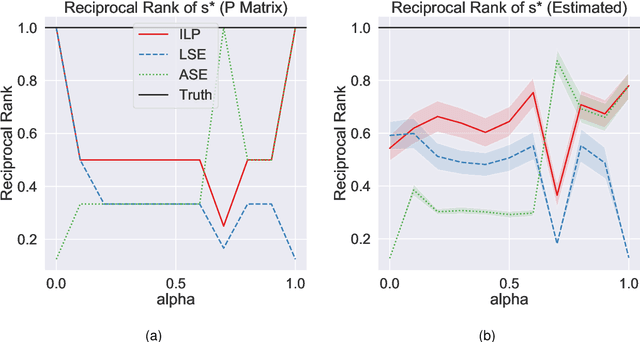
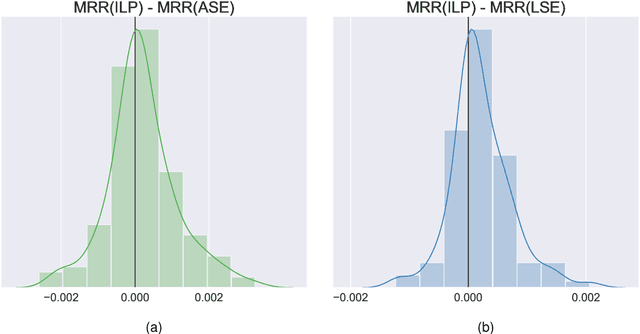
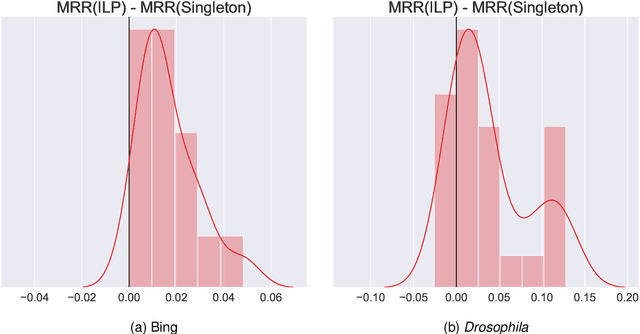
Learning to rank -- producing a ranked list of items specific to a query and with respect to a set of supervisory items -- is a problem of general interest. The setting we consider is one in which no analytic description of what constitutes a good ranking is available. Instead, we have a collection of representations and supervisory information consisting of a (target item, interesting items set) pair. We demonstrate -- analytically, in simulation, and in real data examples -- that learning to rank via combining representations using an integer linear program is effective when the supervision is as light as "these few items are similar to your item of interest." While this nomination task is of general interest, for specificity we present our methodology from the perspective of vertex nomination in graphs. The methodology described herein is model agnostic.

On a 'Two Truths' Phenomenon in Spectral Graph Clustering

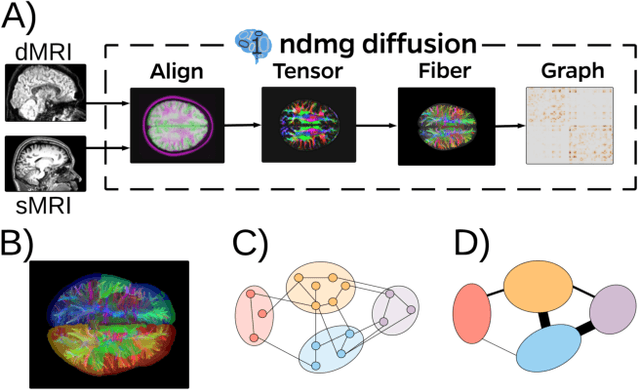
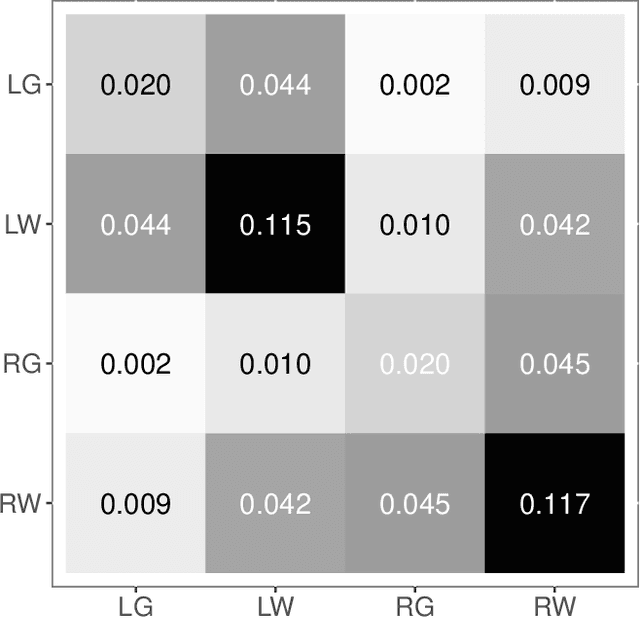
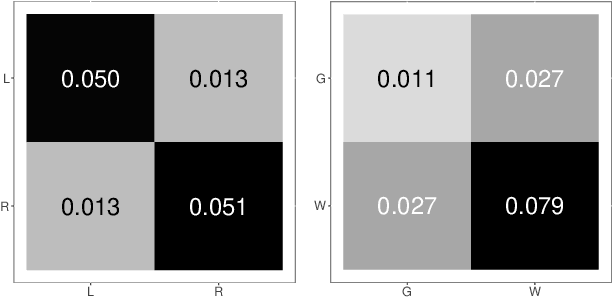
Clustering is concerned with coherently grouping observations without any explicit concept of true groupings. Spectral graph clustering - clustering the vertices of a graph based on their spectral embedding - is commonly approached via K-means (or, more generally, Gaussian mixture model) clustering composed with either Laplacian or Adjacency spectral embedding (LSE or ASE). Recent theoretical results provide new understanding of the problem and solutions, and lead us to a 'Two Truths' LSE vs. ASE spectral graph clustering phenomenon convincingly illustrated here via a diffusion MRI connectome data set: the different embedding methods yield different clustering results, with LSE capturing left hemisphere/right hemisphere affinity structure and ASE capturing gray matter/white matter core-periphery structure.

Statistical inference on random dot product graphs: a survey

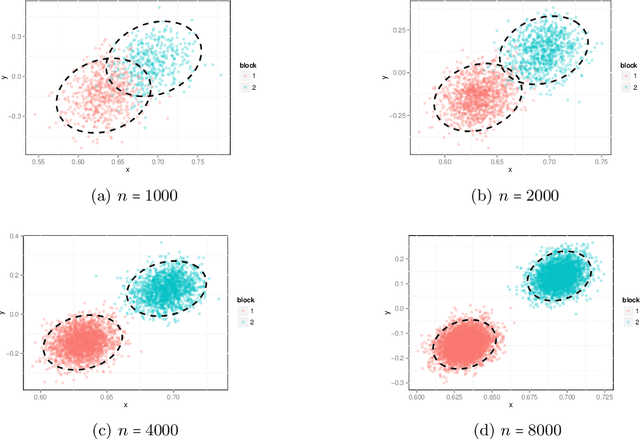
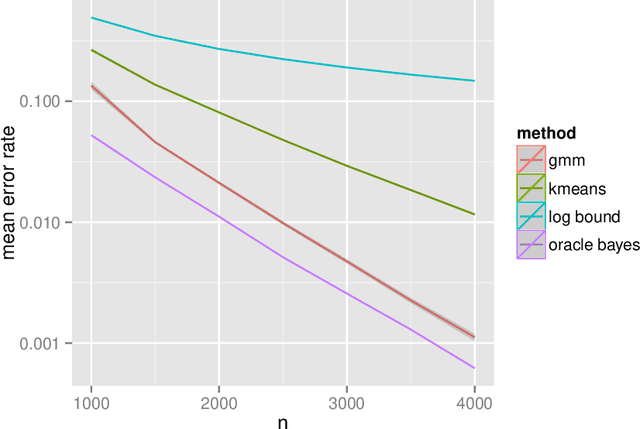
The random dot product graph (RDPG) is an independent-edge random graph that is analytically tractable and, simultaneously, either encompasses or can successfully approximate a wide range of random graphs, from relatively simple stochastic block models to complex latent position graphs. In this survey paper, we describe a comprehensive paradigm for statistical inference on random dot product graphs, a paradigm centered on spectral embeddings of adjacency and Laplacian matrices. We examine the analogues, in graph inference, of several canonical tenets of classical Euclidean inference: in particular, we summarize a body of existing results on the consistency and asymptotic normality of the adjacency and Laplacian spectral embeddings, and the role these spectral embeddings can play in the construction of single- and multi-sample hypothesis tests for graph data. We investigate several real-world applications, including community detection and classification in large social networks and the determination of functional and biologically relevant network properties from an exploratory data analysis of the Drosophila connectome. We outline requisite background and current open problems in spectral graph inference.

Semiparametric spectral modeling of the Drosophila connectome

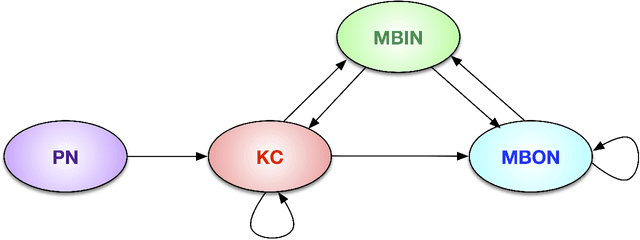
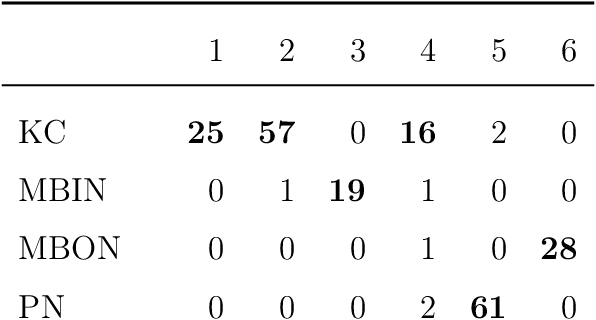
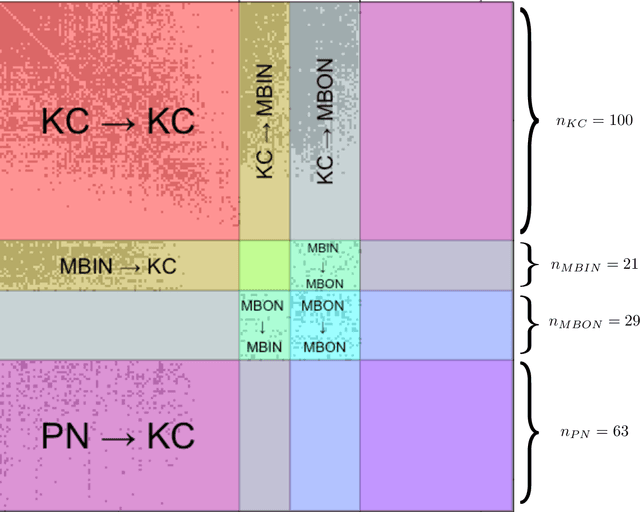
We present semiparametric spectral modeling of the complete larval Drosophila mushroom body connectome. Motivated by a thorough exploratory data analysis of the network via Gaussian mixture modeling (GMM) in the adjacency spectral embedding (ASE) representation space, we introduce the latent structure model (LSM) for network modeling and inference. LSM is a generalization of the stochastic block model (SBM) and a special case of the random dot product graph (RDPG) latent position model, and is amenable to semiparametric GMM in the ASE representation space. The resulting connectome code derived via semiparametric GMM composed with ASE captures latent connectome structure and elucidates biologically relevant neuronal properties.

Community Detection and Classification in Hierarchical Stochastic Blockmodels

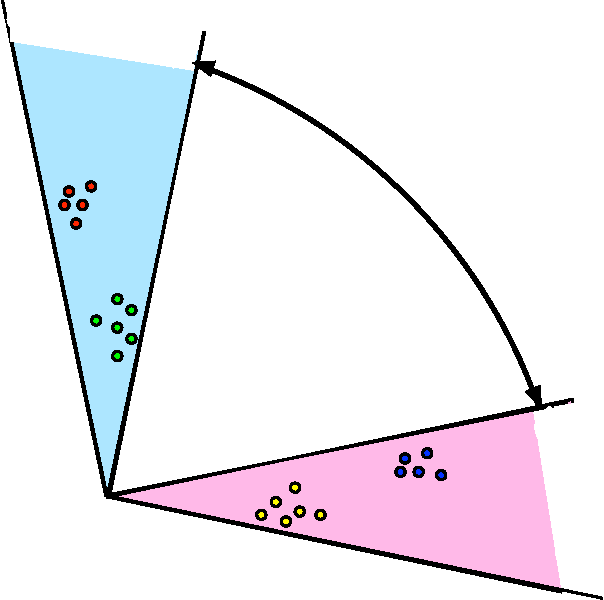
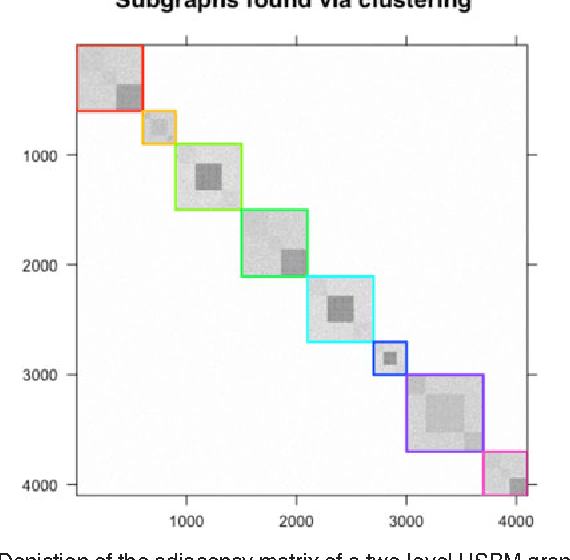
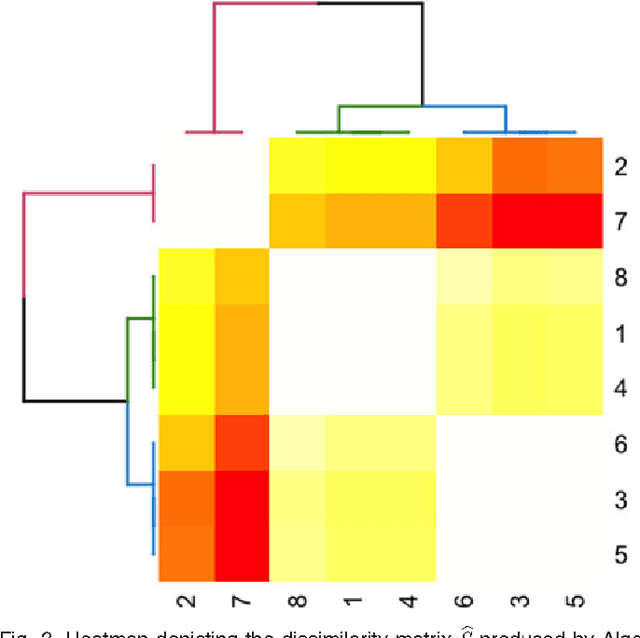
We propose a robust, scalable, integrated methodology for community detection and community comparison in graphs. In our procedure, we first embed a graph into an appropriate Euclidean space to obtain a low-dimensional representation, and then cluster the vertices into communities. We next employ nonparametric graph inference techniques to identify structural similarity among these communities. These two steps are then applied recursively on the communities, allowing us to detect more fine-grained structure. We describe a hierarchical stochastic blockmodel---namely, a stochastic blockmodel with a natural hierarchical structure---and establish conditions under which our algorithm yields consistent estimates of model parameters and motifs, which we define to be stochastically similar groups of subgraphs. Finally, we demonstrate the effectiveness of our algorithm in both simulated and real data. Specifically, we address the problem of locating similar subcommunities in a partially reconstructed Drosophila connectome and in the social network Friendster.

Perfect Clustering for Stochastic Blockmodel Graphs via Adjacency Spectral Embedding

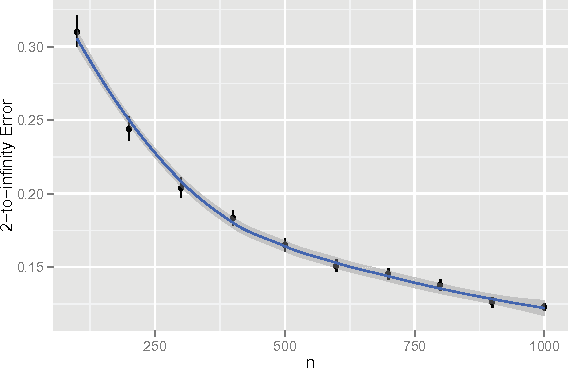
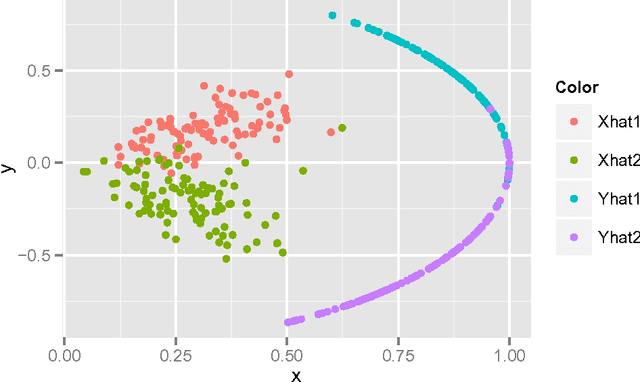
Vertex clustering in a stochastic blockmodel graph has wide applicability and has been the subject of extensive research. In thispaper, we provide a short proof that the adjacency spectral embedding can be used to obtain perfect clustering for the stochastic blockmodel and the degree-corrected stochastic blockmodel. We also show an analogous result for the more general random dot product graph model.

A central limit theorem for scaled eigenvectors of random dot product graphs

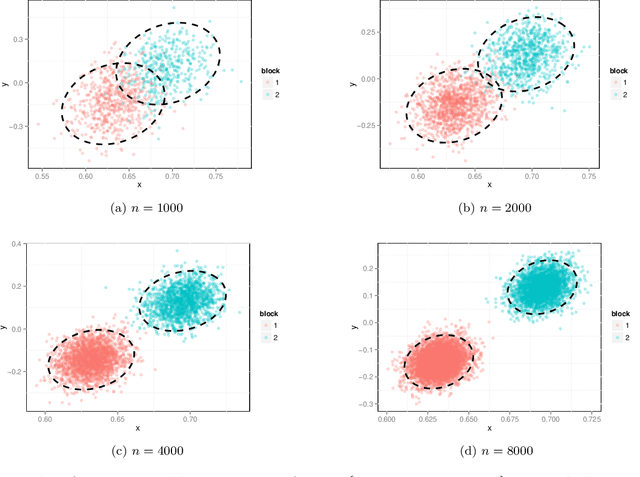
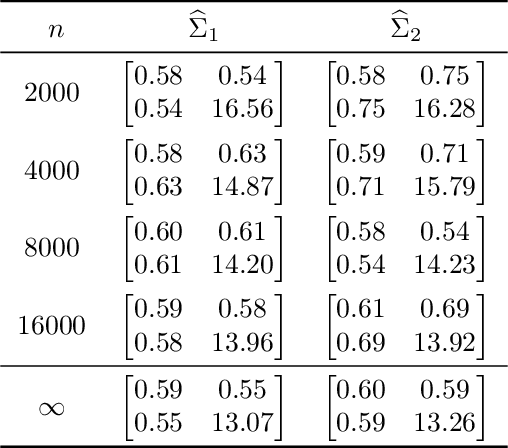
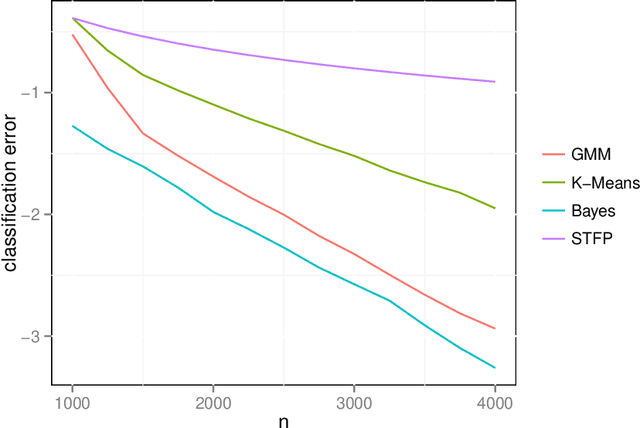
We prove a central limit theorem for the components of the largest eigenvectors of the adjacency matrix of a finite-dimensional random dot product graph whose true latent positions are unknown. In particular, we follow the methodology outlined in \citet{sussman2012universally} to construct consistent estimates for the latent positions, and we show that the appropriately scaled differences between the estimated and true latent positions converge to a mixture of Gaussian random variables. As a corollary, we obtain a central limit theorem for the first eigenvector of the adjacency matrix of an Erd\"os-Renyi random graph.