Prospective Learning in Retrospect

In most real-world applications of artificial intelligence, the distributions of the data and the goals of the learners tend to change over time. The Probably Approximately Correct (PAC) learning framework, which underpins most machine learning algorithms, fails to account for dynamic data distributions and evolving objectives, often resulting in suboptimal performance. Prospective learning is a recently introduced mathematical framework that overcomes some of these limitations. We build on this framework to present preliminary results that improve the algorithm and numerical results, and extend prospective learning to sequential decision-making scenarios, specifically foraging. Code is available at: https://github.com/neurodata/prolearn2.

Learning sources of variability from high-dimensional observational studies

Causal inference studies whether the presence of a variable influences an observed outcome. As measured by quantities such as the "average treatment effect," this paradigm is employed across numerous biological fields, from vaccine and drug development to policy interventions. Unfortunately, the majority of these methods are often limited to univariate outcomes. Our work generalizes causal estimands to outcomes with any number of dimensions or any measurable space, and formulates traditional causal estimands for nominal variables as causal discrepancy tests. We propose a simple technique for adjusting universally consistent conditional independence tests and prove that these tests are universally consistent causal discrepancy tests. Numerical experiments illustrate that our method, Causal CDcorr, leads to improvements in both finite sample validity and power when compared to existing strategies. Our methods are all open source and available at github.com/ebridge2/cdcorr.

Polarity is all you need to learn and transfer faster

Natural intelligences (NIs) thrive in a dynamic world - they learn quickly, sometimes with only a few samples. In contrast, Artificial intelligences (AIs) typically learn with prohibitive amount of training samples and computational power. What design principle difference between NI and AI could contribute to such a discrepancy? Here, we propose an angle from weight polarity: development processes initialize NIs with advantageous polarity configurations; as NIs grow and learn, synapse magnitudes update yet polarities are largely kept unchanged. We demonstrate with simulation and image classification tasks that if weight polarities are adequately set $\textit{a priori}$, then networks learn with less time and data. We also explicitly illustrate situations in which $\textit{a priori}$ setting the weight polarities is disadvantageous for networks. Our work illustrates the value of weight polarities from the perspective of statistical and computational efficiency during learning.

Approximately optimal domain adaptation with Fisher's Linear Discriminant Analysis

We propose a class of models based on Fisher's Linear Discriminant (FLD) in the context of domain adaptation. The class is the convex combination of two hypotheses: i) an average hypothesis representing previously seen source tasks and ii) a hypothesis trained on a new target task. For a particular generative setting we derive the optimal convex combination of the two models under 0-1 loss, propose a computable approximation, and study the effect of various parameter settings on the relative risks between the optimal hypothesis, hypothesis i), and hypothesis ii). We demonstrate the effectiveness of the proposed optimal classifier in the context of EEG- and ECG-based classification settings and argue that the optimal classifier can be computed without access to direct information from any of the individual source tasks. We conclude by discussing further applications, limitations, and possible future directions.

The Value of Out-of-Distribution Data

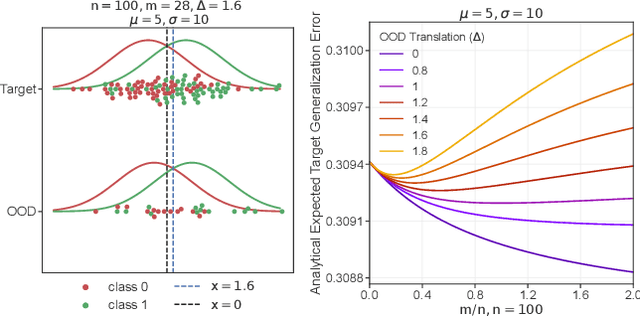
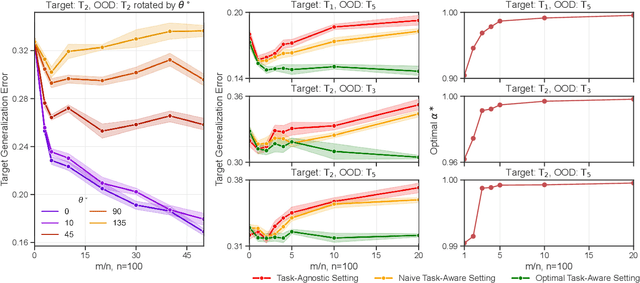
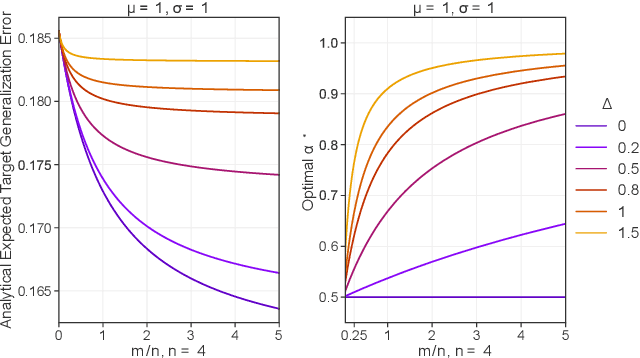
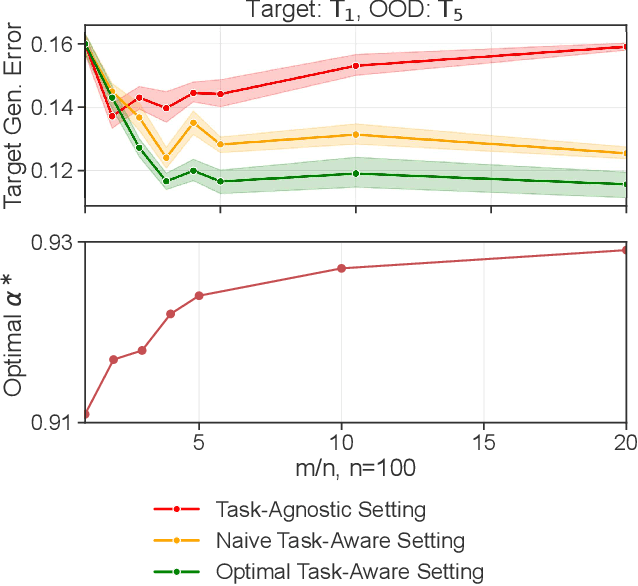
More data helps us generalize to a task. But real datasets can contain out-of-distribution (OOD) data; this can come in the form of heterogeneity such as intra-class variability but also in the form of temporal shifts or concept drifts. We demonstrate a counter-intuitive phenomenon for such problems: generalization error of the task can be a non-monotonic function of the number of OOD samples; a small number of OOD samples can improve generalization but if the number of OOD samples is beyond a threshold, then the generalization error can deteriorate. We also show that if we know which samples are OOD, then using a weighted objective between the target and OOD samples ensures that the generalization error decreases monotonically. We demonstrate and analyze this issue using linear classifiers on synthetic datasets and medium-sized neural networks on CIFAR-10.

Why Do Networks Need Negative Weights?

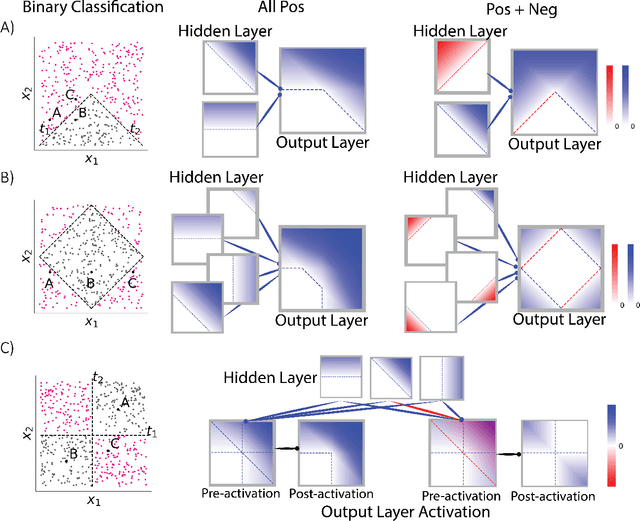
Why do networks have negative weights at all? The answer is: to learn more functions. We mathematically prove that deep neural networks with all non-negative weights are not universal approximators. This fundamental result is assumed by much of the deep learning literature without previously proving the result and demonstrating its necessity.

Out-of-distribution and in-distribution posterior calibration using Kernel Density Polytopes

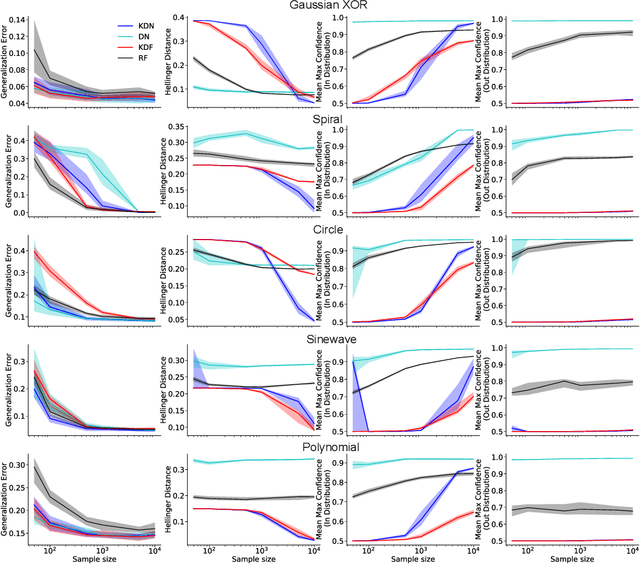
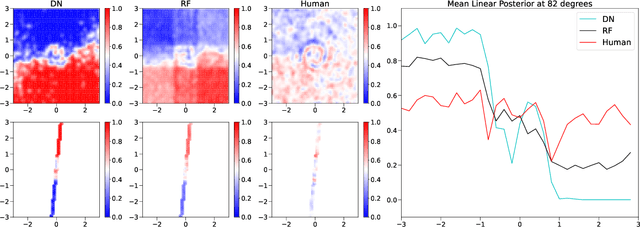
Any reasonable machine learning (ML) model should not only interpolate efficiently in between the training samples provided (in-distribution region), but also approach the extrapolative or out-of-distribution (OOD) region without being overconfident. Our experiment on human subjects justifies the aforementioned properties for human intelligence as well. Many state-of-the-art algorithms have tried to fix the overconfidence problem of ML models in the OOD region. However, in doing so, they have often impaired the in-distribution performance of the model. Our key insight is that ML models partition the feature space into polytopes and learn constant (random forests) or affine (ReLU networks) functions over those polytopes. This leads to the OOD overconfidence problem for the polytopes which lie in the training data boundary and extend to infinity. To resolve this issue, we propose kernel density methods that fit Gaussian kernel over the polytopes, which are learned using ML models. Specifically, we introduce two variants of kernel density polytopes: Kernel Density Forest (KDF) and Kernel Density Network (KDN) based on random forests and deep networks, respectively. Studies on various simulation settings show that both KDF and KDN achieve uniform confidence over the classes in the OOD region while maintaining good in-distribution accuracy compared to that of their respective parent models.

Prospective Learning: Back to the Future

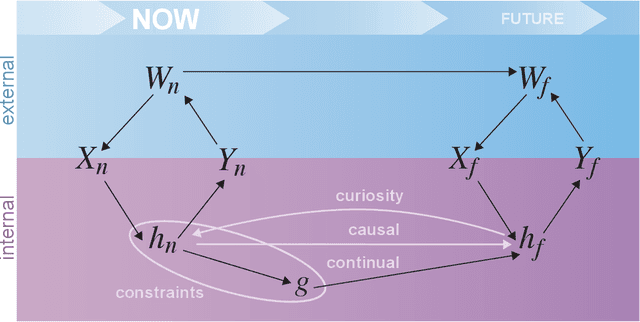
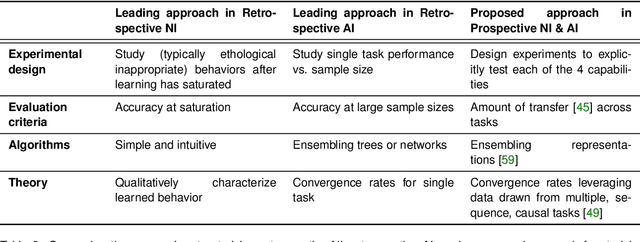
Research on both natural intelligence (NI) and artificial intelligence (AI) generally assumes that the future resembles the past: intelligent agents or systems (what we call 'intelligence') observe and act on the world, then use this experience to act on future experiences of the same kind. We call this 'retrospective learning'. For example, an intelligence may see a set of pictures of objects, along with their names, and learn to name them. A retrospective learning intelligence would merely be able to name more pictures of the same objects. We argue that this is not what true intelligence is about. In many real world problems, both NIs and AIs will have to learn for an uncertain future. Both must update their internal models to be useful for future tasks, such as naming fundamentally new objects and using these objects effectively in a new context or to achieve previously unencountered goals. This ability to learn for the future we call 'prospective learning'. We articulate four relevant factors that jointly define prospective learning. Continual learning enables intelligences to remember those aspects of the past which it believes will be most useful in the future. Prospective constraints (including biases and priors) facilitate the intelligence finding general solutions that will be applicable to future problems. Curiosity motivates taking actions that inform future decision making, including in previously unmet situations. Causal estimation enables learning the structure of relations that guide choosing actions for specific outcomes, even when the specific action-outcome contingencies have never been observed before. We argue that a paradigm shift from retrospective to prospective learning will enable the communities that study intelligence to unite and overcome existing bottlenecks to more effectively explain, augment, and engineer intelligences.

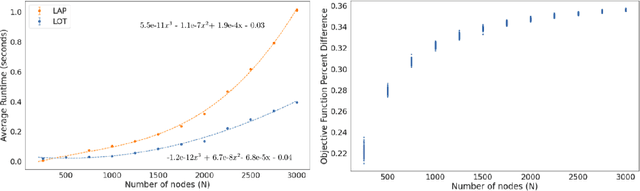
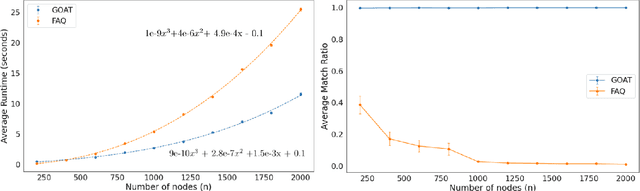
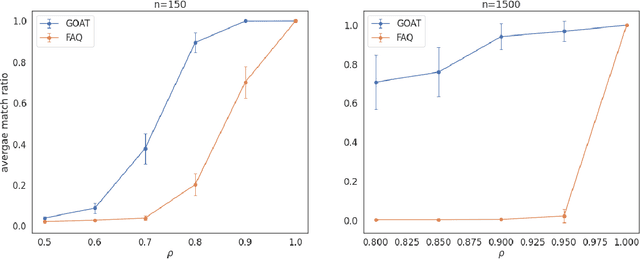
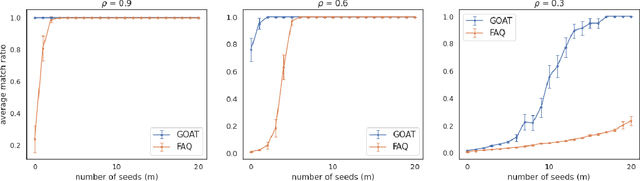
Graph Matching via Optimal Transport

The graph matching problem seeks to find an alignment between the nodes of two graphs that minimizes the number of adjacency disagreements. Solving the graph matching is increasingly important due to it's applications in operations research, computer vision, neuroscience, and more. However, current state-of-the-art algorithms are inefficient in matching very large graphs, though they produce good accuracy. The main computational bottleneck of these algorithms is the linear assignment problem, which must be solved at each iteration. In this paper, we leverage the recent advances in the field of optimal transport to replace the accepted use of linear assignment algorithms. We present GOAT, a modification to the state-of-the-art graph matching approximation algorithm "FAQ" (Vogelstein, 2015), replacing its linear sum assignment step with the "Lightspeed Optimal Transport" method of Cuturi (2013). The modification provides improvements to both speed and empirical matching accuracy. The effectiveness of the approach is demonstrated in matching graphs in simulated and real data examples.

Streaming Decision Trees and Forests

Machine learning has successfully leveraged modern data and provided computational solutions to innumerable real-world problems, including physical and biomedical discoveries. Currently, estimators could handle both scenarios with all samples available and situations requiring continuous updates. However, there is still room for improvement on streaming algorithms based on batch decision trees and random forests, which are the leading methods in batch data tasks. In this paper, we explore the simplest partial fitting algorithm to extend batch trees and test our models: stream decision tree (SDT) and stream decision forest (SDF) on three classification tasks of varying complexities. For reference, both existing streaming trees (Hoeffding trees and Mondrian forests) and batch estimators are included in the experiments. In all three tasks, SDF consistently produces high accuracy, whereas existing estimators encounter space restraints and accuracy fluctuations. Thus, our streaming trees and forests show great potential for further improvements, which are good candidates for solving problems like distribution drift and transfer learning.