Regression for matrix-valued data via Kronecker products factorization

We study the matrix-variate regression problem $Y_i = \sum_{k} \beta_{1k} X_i \beta_{2k}^{\top} + E_i$ for $i=1,2\dots,n$ in the high dimensional regime wherein the response $Y_i$ are matrices whose dimensions $p_{1}\times p_{2}$ outgrow both the sample size $n$ and the dimensions $q_{1}\times q_{2}$ of the predictor variables $X_i$ i.e., $q_{1},q_{2} \ll n \ll p_{1},p_{2}$. We propose an estimation algorithm, termed KRO-PRO-FAC, for estimating the parameters $\{\beta_{1k}\} \subset \Re^{p_1 \times q_1}$ and $\{\beta_{2k}\} \subset \Re^{p_2 \times q_2}$ that utilizes the Kronecker product factorization and rearrangement operations from Van Loan and Pitsianis (1993). The KRO-PRO-FAC algorithm is computationally efficient as it does not require estimating the covariance between the entries of the $\{Y_i\}$. We establish perturbation bounds between $\hat{\beta}_{1k} -\beta_{1k}$ and $\hat{\beta}_{2k} - \beta_{2k}$ in spectral norm for the setting where either the rows of $E_i$ or the columns of $E_i$ are independent sub-Gaussian random vectors. Numerical studies on simulated and real data indicate that our procedure is competitive, in terms of both estimation error and predictive accuracy, compared to other existing methods.

Adversarial contamination of networks in the setting of vertex nomination: a new trimming method

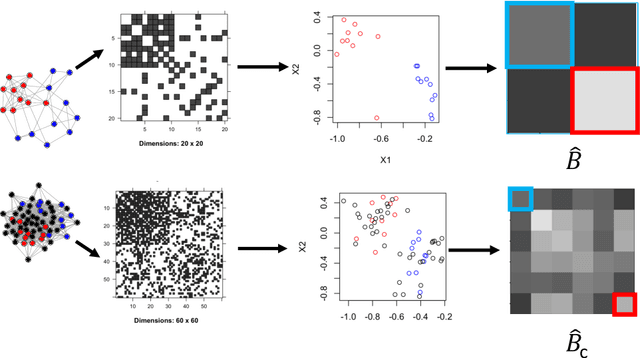
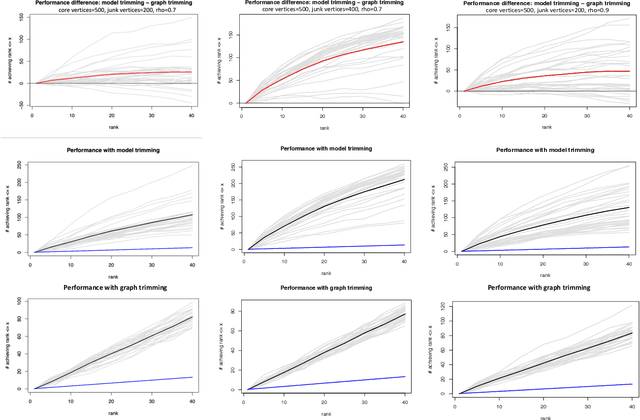
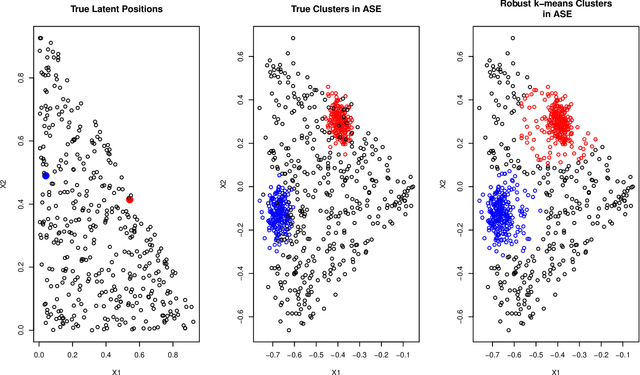
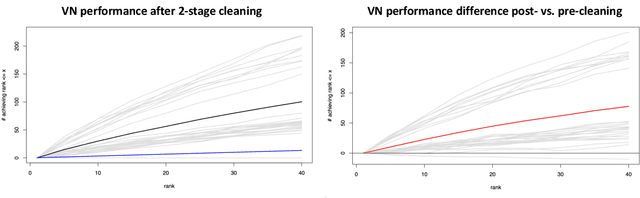
As graph data becomes more ubiquitous, the need for robust inferential graph algorithms to operate in these complex data domains is crucial. In many cases of interest, inference is further complicated by the presence of adversarial data contamination. The effect of the adversary is frequently to change the data distribution in ways that negatively affect statistical and algorithmic performance. We study this phenomenon in the context of vertex nomination, a semi-supervised information retrieval task for network data. Here, a common suite of methods relies on spectral graph embeddings, which have been shown to provide both good algorithmic performance and flexible settings in which regularization techniques can be implemented to help mitigate the effect of an adversary. Many current regularization methods rely on direct network trimming to effectively excise the adversarial contamination, although this direct trimming often gives rise to complicated dependency structures in the resulting graph. We propose a new trimming method that operates in model space which can address both block structure contamination and white noise contamination (contamination whose distribution is unknown). This model trimming is more amenable to theoretical analysis while also demonstrating superior performance in a number of simulations, compared to direct trimming.

Perturbation Analysis of Randomized SVD and its Applications to High-dimensional Statistics

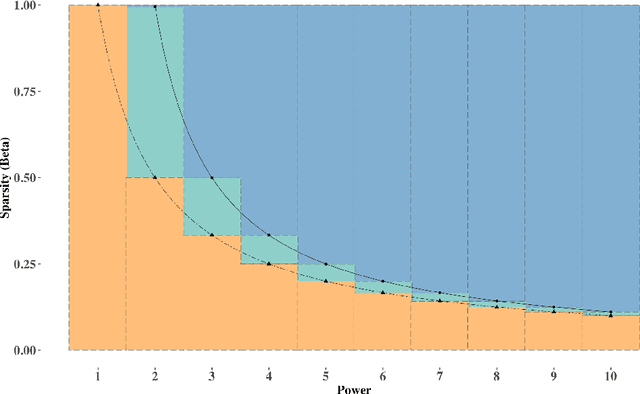
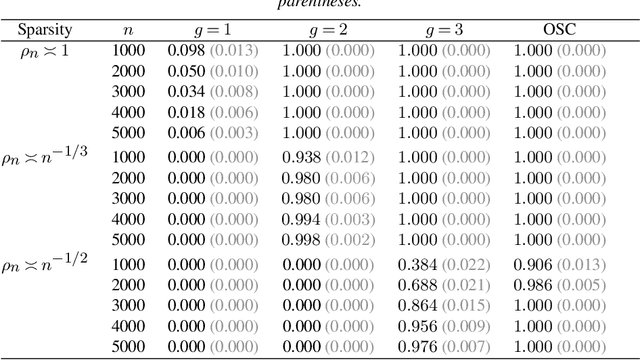
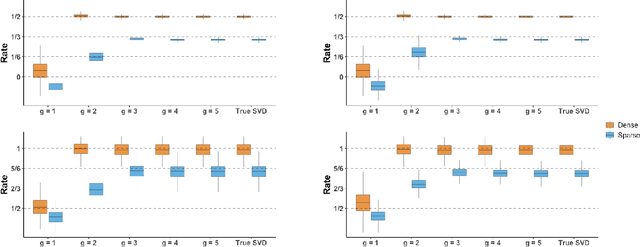
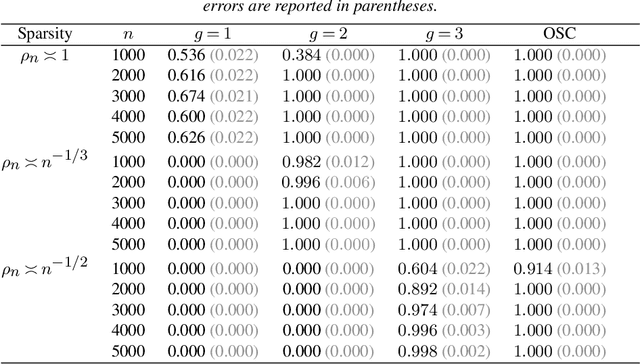
Randomized singular value decomposition (RSVD) is a class of computationally efficient algorithms for computing the truncated SVD of large data matrices. Given a $n \times n$ symmetric matrix $\mathbf{M}$, the prototypical RSVD algorithm outputs an approximation of the $k$ leading singular vectors of $\mathbf{M}$ by computing the SVD of $\mathbf{M}^{g} \mathbf{G}$; here $g \geq 1$ is an integer and $\mathbf{G} \in \mathbb{R}^{n \times k}$ is a random Gaussian sketching matrix. In this paper we study the statistical properties of RSVD under a general "signal-plus-noise" framework, i.e., the observed matrix $\hat{\mathbf{M}}$ is assumed to be an additive perturbation of some true but unknown signal matrix $\mathbf{M}$. We first derive upper bounds for the $\ell_2$ (spectral norm) and $\ell_{2\to\infty}$ (maximum row-wise $\ell_2$ norm) distances between the approximate singular vectors of $\hat{\mathbf{M}}$ and the true singular vectors of the signal matrix $\mathbf{M}$. These upper bounds depend on the signal-to-noise ratio (SNR) and the number of power iterations $g$. A phase transition phenomenon is observed in which a smaller SNR requires larger values of $g$ to guarantee convergence of the $\ell_2$ and $\ell_{2\to\infty}$ distances. We also show that the thresholds for $g$ where these phase transitions occur are sharp whenever the noise matrices satisfy a certain trace growth condition. Finally, we derive normal approximations for the row-wise fluctuations of the approximate singular vectors and the entrywise fluctuations of the approximate matrix. We illustrate our theoretical results by deriving nearly-optimal performance guarantees for RSVD when applied to three statistical inference problems, namely, community detection, matrix completion, and principal component analysis with missing data.

Classification of high-dimensional data with spiked covariance matrix structure

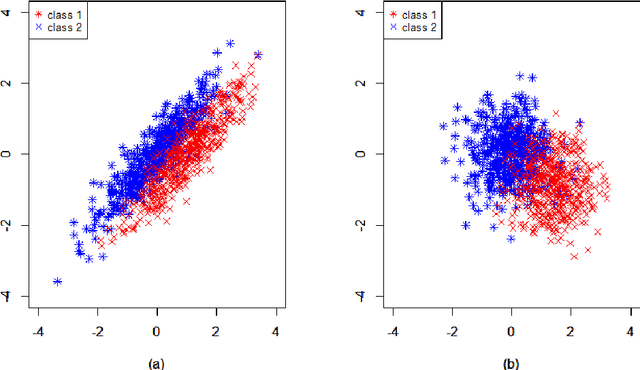
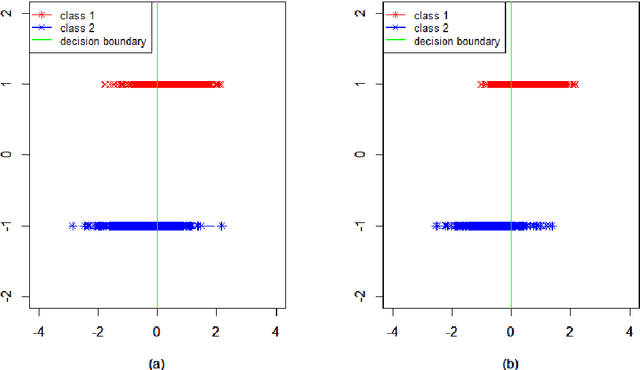
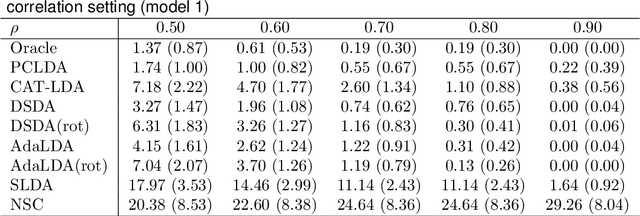
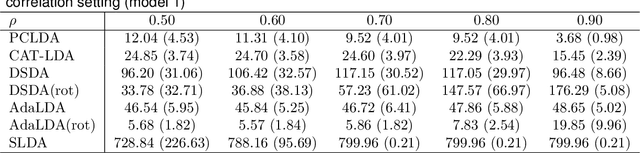
We study the classification problem for high-dimensional data with $n$ observations on $p$ features where the $p \times p$ covariance matrix $\Sigma$ exhibits a spiked eigenvalues structure and the vector $\zeta$, given by the difference between the whitened mean vectors, is sparse with sparsity at most $s$. We propose an adaptive classifier (adaptive with respect to the sparsity $s$) that first performs dimension reduction on the feature vectors prior to classification in the dimensionally reduced space, i.e., the classifier whitened the data, then screen the features by keeping only those corresponding to the $s$ largest coordinates of $\zeta$ and finally apply Fisher linear discriminant on the selected features. Leveraging recent results on entrywise matrix perturbation bounds for covariance matrices, we show that the resulting classifier is Bayes optimal whenever $n \rightarrow \infty$ and $s \sqrt{n^{-1} \ln p} \rightarrow 0$. Experimental results on real and synthetic data sets indicate that the proposed classifier is competitive with existing state-of-the-art methods while also selecting a smaller number of features.

Popularity Adjusted Block Models are Generalized Random Dot Product Graphs

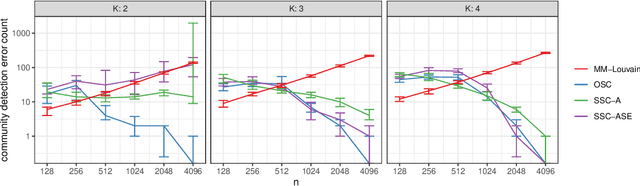
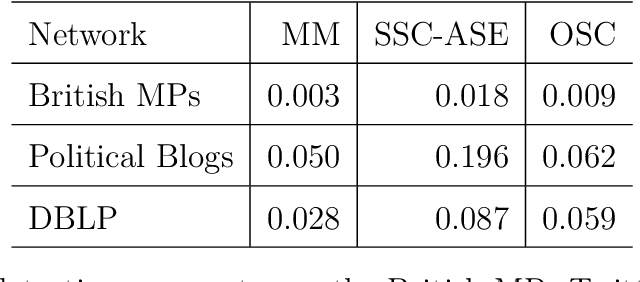
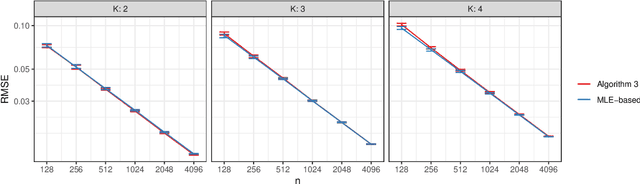
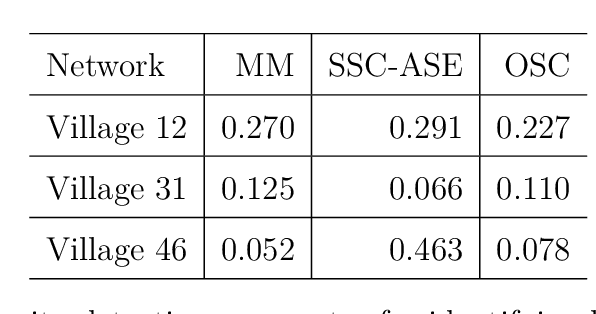
We connect two random graph models, the Popularity Adjusted Block Model (PABM) and the Generalized Random Dot Product Graph (GRDPG), by demonstrating that the PABM is a special case of the GRDPG in which communities correspond to mutually orthogonal subspaces of latent vectors. This insight allows us to construct new algorithms for community detection and parameter estimation for the PABM, as well as improve an existing algorithm that relies on Sparse Subspace Clustering. Using established asymptotic properties of Adjacency Spectral Embedding for the GRDPG, we derive asymptotic properties of these algorithms. In particular, we demonstrate that the absolute number of community detection errors tends to zero as the number of graph vertices tends to infinity. Simulation experiments illustrate these properties.

Hypothesis Testing for Equality of Latent Positions in Random Graphs

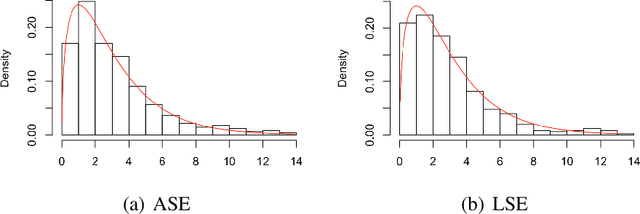
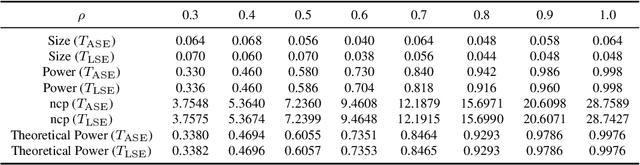
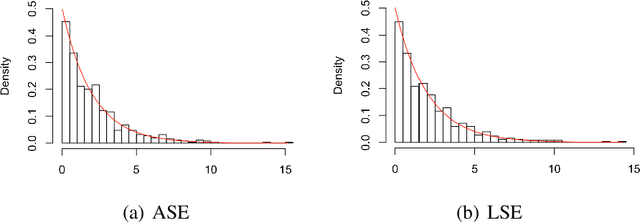
We consider the hypothesis testing problem that two vertices $i$ and $j$ of a generalized random dot product graph have the same latent positions, possibly up to scaling. Special cases of this hypotheses test include testing whether two vertices in a stochastic block model or degree-corrected stochastic block model graph have the same block membership vectors. We propose several test statistics based on the empirical Mahalanobis distances between the $i$th and $j$th rows of either the adjacency or the normalized Laplacian spectral embedding of the graph. We show that, under mild conditions, these test statistics have limiting chi-square distributions under both the null and local alternative hypothesis, and we derived explicit expressions for the non-centrality parameters under the local alternative. Using these limit results, we address the model selection problem of choosing between the standard stochastic block model and its degree-corrected variant. The effectiveness of our proposed tests are illustrated via both simulation studies and real data applications.

Consistency of random-walk based network embedding algorithms

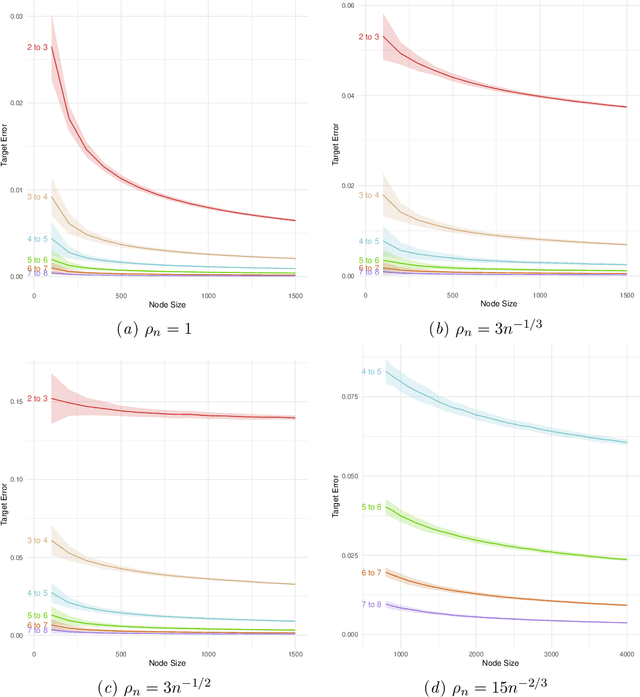
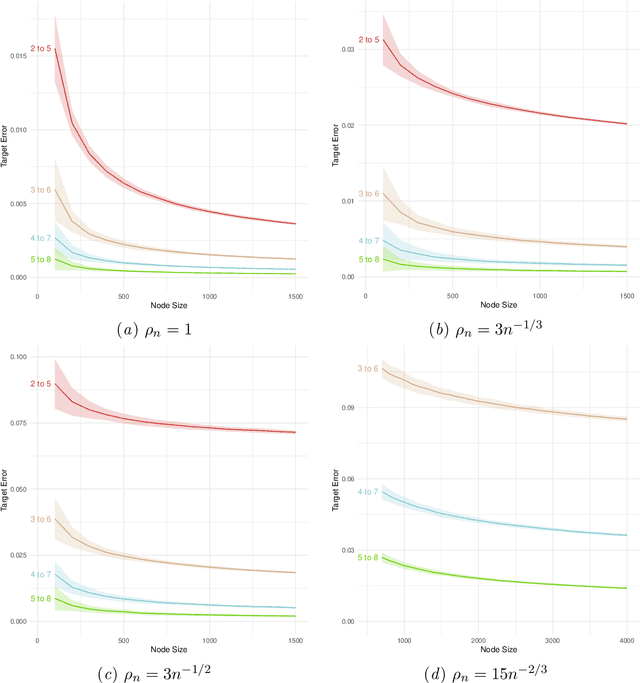
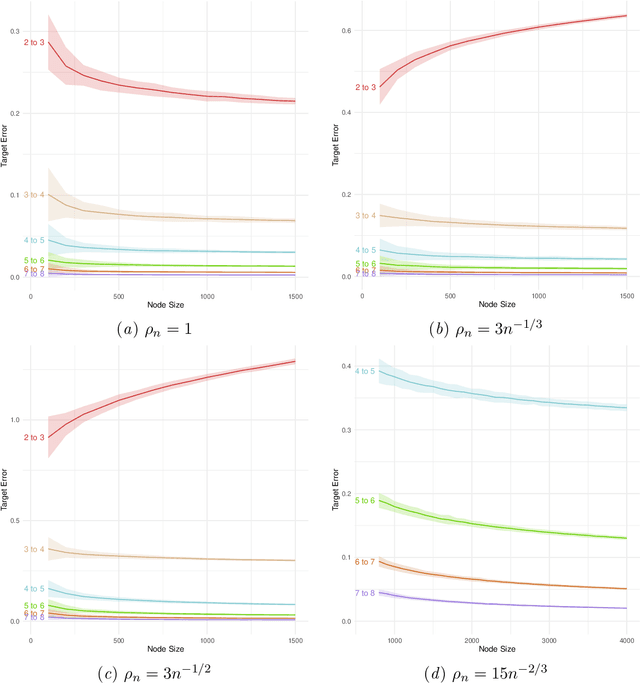
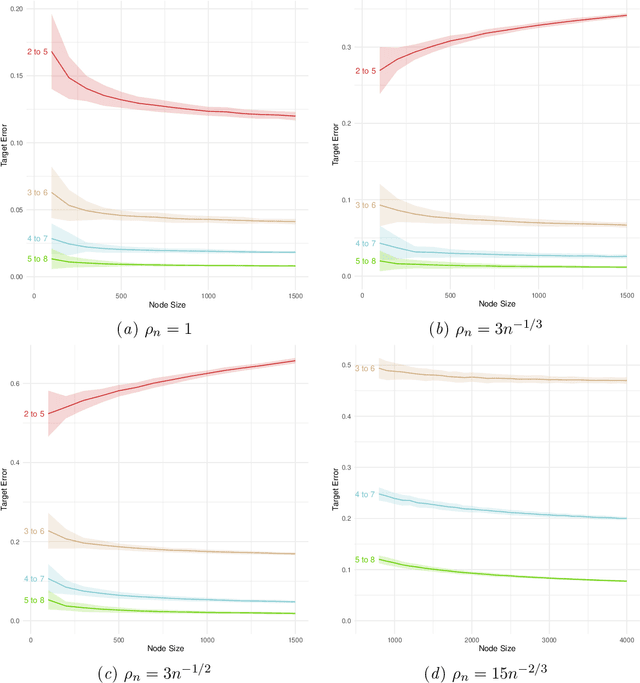
Random-walk based network embedding algorithms like node2vec and DeepWalk are widely used to obtain Euclidean representation of the nodes in a network prior to performing down-stream network inference tasks. Nevertheless, despite their impressive empirical performance, there is a lack of theoretical results explaining their behavior. In this paper we studied the node2vec and DeepWalk algorithms through the perspective of matrix factorization. We analyze these algorithms in the setting of community detection for stochastic blockmodel graphs; in particular we established large-sample error bounds and prove consistent community recovery of node2vec/DeepWalk embedding followed by k-means clustering. Our theoretical results indicate a subtle interplay between the sparsity of the observed networks, the window sizes of the random walks, and the convergence rates of the node2vec/DeepWalk embedding toward the embedding of the true but unknown edge probabilities matrix. More specifically, as the network becomes sparser, our results suggest using larger window sizes, or equivalently, taking longer random walks, in order to attain better convergence rate for the resulting embeddings. The paper includes numerical experiments corroborating these observations.

Learning 1-Dimensional Submanifolds for Subsequent Inference on Random Dot Product Graphs

A random dot product graph (RDPG) is a generative model for networks in which vertices correspond to positions in a latent Euclidean space and edge probabilities are determined by the dot products of the latent positions. We consider RDPGs for which the latent positions are randomly sampled from an unknown $1$-dimensional submanifold of the latent space. In principle, restricted inference, i.e., procedures that exploit the structure of the submanifold, should be more effective than unrestricted inference; however, it is not clear how to conduct restricted inference when the submanifold is unknown. We submit that techniques for manifold learning can be used to learn the unknown submanifold well enough to realize benefit from restricted inference. To illustrate, we test a hypothesis about the Fr\'{e}chet mean of a small community of vertices, using the complete set of vertices to infer latent structure. We propose test statistics that deploy the Isomap procedure for manifold learning, using shortest path distances on neighborhood graphs constructed from estimated latent positions to estimate arc lengths on the unknown $1$-dimensional submanifold. Unlike conventional applications of Isomap, the estimated latent positions do not lie on the submanifold of interest. We extend existing convergence results for Isomap to this setting and use them to demonstrate that, as the number of auxiliary vertices increases, the power of our test converges to the power of the corresponding test when the submanifold is known.

On Two Distinct Sources of Nonidentifiability in Latent Position Random Graph Models

Two separate and distinct sources of nonidentifiability arise naturally in the context of latent position random graph models, though neither are unique to this setting. In this paper we define and examine these two nonidentifiabilities, dubbed subspace nonidentifiability and model-based nonidentifiability, in the context of random graph inference. We give examples where each type of nonidentifiability comes into play, and we show how in certain settings one need worry about one or the other type of nonidentifiability. Then, we characterize the limit for model-based nonidentifiability both with and without subspace nonidentifiability. We further obtain additional limiting results for covariances and $U$-statistics of stochastic block models and generalized random dot product graphs.

Limit theorems for out-of-sample extensions of the adjacency and Laplacian spectral embeddings

Graph embeddings, a class of dimensionality reduction techniques designed for relational data, have proven useful in exploring and modeling network structure. Most dimensionality reduction methods allow out-of-sample extensions, by which an embedding can be applied to observations not present in the training set. Applied to graphs, the out-of-sample extension problem concerns how to compute the embedding of a vertex that is added to the graph after an embedding has already been computed. In this paper, we consider the out-of-sample extension problem for two graph embedding procedures: the adjacency spectral embedding and the Laplacian spectral embedding. In both cases, we prove that when the underlying graph is generated according to a latent space model called the random dot product graph, which includes the popular stochastic block model as a special case, an out-of-sample extension based on a least-squares objective obeys a central limit theorem about the true latent position of the out-of-sample vertex. In addition, we prove a concentration inequality for the out-of-sample extension of the adjacency spectral embedding based on a maximum-likelihood objective. Our results also yield a convenient framework in which to analyze trade-offs between estimation accuracy and computational expense, which we explore briefly.