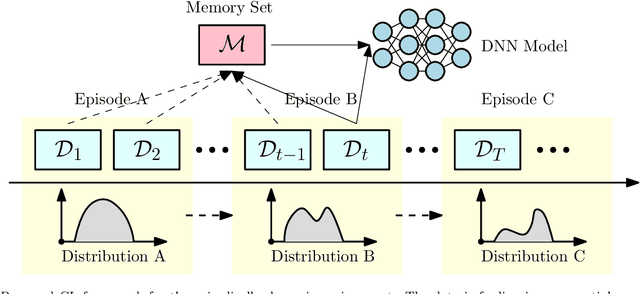
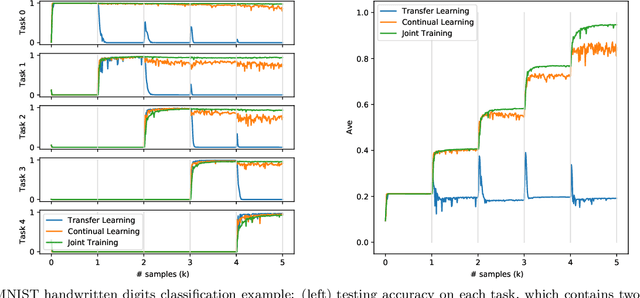
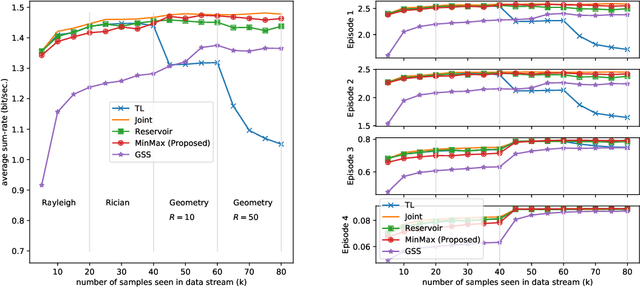
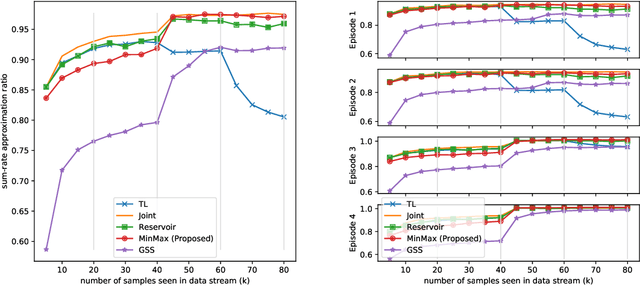
Learning to Continuously Optimize Wireless Resource In Episodically Dynamic Environment

There has been a growing interest in developing data-driven and in particular deep neural network (DNN) based methods for modern communication tasks. For a few popular tasks such as power control, beamforming, and MIMO detection, these methods achieve state-of-the-art performance while requiring less computational efforts, less channel state information (CSI), etc. However, it is often challenging for these approaches to learn in a dynamic environment where parameters such as CSIs keep changing. This work develops a methodology that enables data-driven methods to continuously learn and optimize in a dynamic environment. Specifically, we consider an ``episodically dynamic" setting where the environment changes in ``episodes", and in each episode the environment is stationary. We propose to build the notion of continual learning (CL) into the modeling process of learning wireless systems, so that the learning model can incrementally adapt to the new episodes, {\it without forgetting} knowledge learned from the previous episodes. Our design is based on a novel min-max formulation which ensures certain ``fairness" across different data samples. We demonstrate the effectiveness of the CL approach by customizing it to two popular DNN based models (one for power control and one for beamforming), and testing using both synthetic and real data sets. These numerical results show that the proposed CL approach is not only able to adapt to the new scenarios quickly and seamlessly, but importantly, it maintains high performance over the previously encountered scenarios as well.

Learning to Beamform in Heterogeneous Massive MIMO Networks

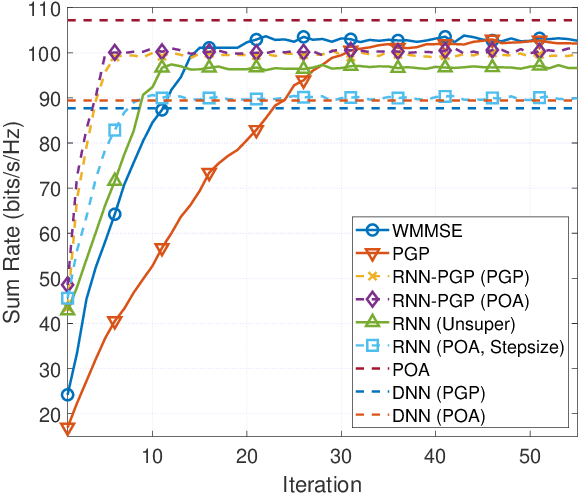
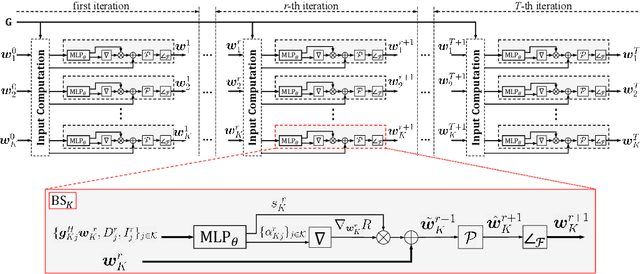
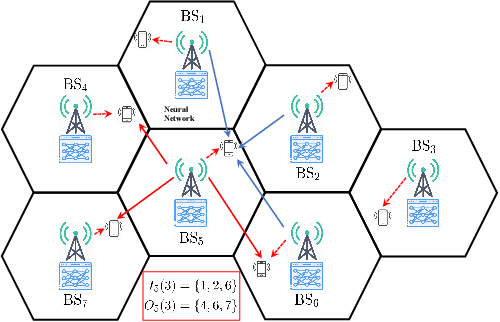
It is well-known that the problem of finding the optimal beamformers in massive multiple-input multiple-output (MIMO) networks is challenging because of its non-convexity, and conventional optimization based algorithms suffer from high computational costs. While computationally efficient deep learning based methods have been proposed, their complexity heavily relies upon system parameters such as the number of transmit antennas, and therefore these methods typically do not generalize well when deployed in heterogeneous scenarios where the base stations (BSs) are equipped with different numbers of transmit antennas and have different inter-BS distances. This paper proposes a novel deep learning based beamforming algorithm to address the above challenges. Specifically, we consider the weighted sum rate (WSR) maximization problem in multi-input and single-output (MISO) interference channels, and propose a deep neural network architecture by unfolding a parallel gradient projection algorithm. Somewhat surprisingly, by leveraging the low-dimensional structures of the optimal beamforming solution, our constructed neural network can be made independent of the numbers of transmit antennas and BSs. Moreover, such a design can be further extended to a cooperative multicell network. Numerical results based on both synthetic and ray-tracing channel models show that the proposed neural network can achieve high WSRs with significantly reduced runtime, while exhibiting favorable generalization capability with respect to the antenna number, BS number and the inter-BS distance.

A Two-Timescale Framework for Bilevel Optimization: Complexity Analysis and Application to Actor-Critic

This paper analyzes a two-timescale stochastic algorithm for a class of bilevel optimization problems with applications such as policy optimization in reinforcement learning, hyperparameter optimization, among others. We consider a case when the inner problem is unconstrained and strongly convex, and the outer problem is either strongly convex, convex or weakly convex. We propose a nonlinear two-timescale stochastic approximation (TTSA) algorithm for tackling the bilevel optimization. In the algorithm, a stochastic (semi)gradient update with a larger step size (faster timescale) is used for the inner problem, while a stochastic mirror descent update with a smaller step size (slower timescale) is used for the outer problem. When the outer problem is strongly convex (resp. weakly convex), the TTSA algorithm finds an $\mathcal{O}(K^{-1/2})$-optimal (resp. $\mathcal{O}(K^{-2/5})$-stationary) solution, where $K$ is the iteration number. To our best knowledge, these are the first convergence rate results for using nonlinear TTSA algorithms on the concerned class of bilevel optimization problems. Lastly, specific to the application of policy optimization, we show that a two-timescale actor-critic proximal policy optimization algorithm can be viewed as a special case of our framework. The actor-critic algorithm converges at $\mathcal{O}(K^{-1/4})$ in terms of the gap in objective value to a globally optimal policy.

Understanding Gradient Clipping in Private SGD: A Geometric Perspective

Deep learning models are increasingly popular in many machine learning applications where the training data may contain sensitive information. To provide formal and rigorous privacy guarantee, many learning systems now incorporate differential privacy by training their models with (differentially) private SGD. A key step in each private SGD update is gradient clipping that shrinks the gradient of an individual example whenever its L2 norm exceeds some threshold. We first demonstrate how gradient clipping can prevent SGD from converging to stationary point. We then provide a theoretical analysis that fully quantifies the clipping bias on convergence with a disparity measure between the gradient distribution and a geometrically symmetric distribution. Our empirical evaluation further suggests that the gradient distributions along the trajectory of private SGD indeed exhibit symmetric structure that favors convergence. Together, our results provide an explanation why private SGD with gradient clipping remains effective in practice despite its potential clipping bias. Finally, we develop a new perturbation-based technique that can provably correct the clipping bias even for instances with highly asymmetric gradient distributions.

Private Stochastic Non-Convex Optimization: Adaptive Algorithms and Tighter Generalization Bounds

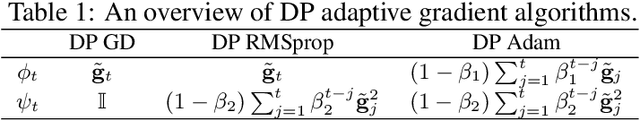
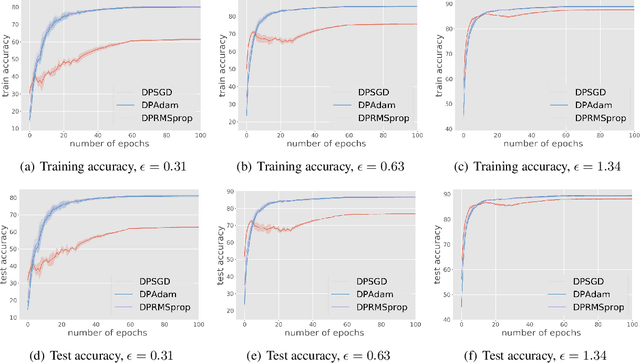
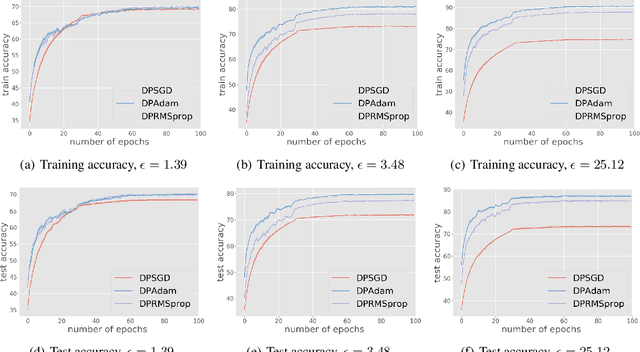
We study differentially private (DP) algorithms for stochastic non-convex optimization. In this problem, the goal is to minimize the population loss over a $p$-dimensional space given $n$ i.i.d. samples drawn from a distribution. We improve upon the population gradient bound of ${\sqrt{p}}/{\sqrt{n}}$ from prior work and obtain a sharper rate of $\sqrt[4]{p}/\sqrt{n}$. We obtain this rate by providing the first analyses on a collection of private gradient-based methods, including adaptive algorithms DP RMSProp and DP Adam. Our proof technique leverages the connection between differential privacy and adaptive data analysis to bound gradient estimation error at every iterate, which circumvents the worse generalization bound from the standard uniform convergence argument. Finally, we evaluate the proposed algorithms on two popular deep learning tasks and demonstrate the empirical advantages of DP adaptive gradient methods over standard DP SGD.

On the Divergence of Decentralized Non-Convex Optimization

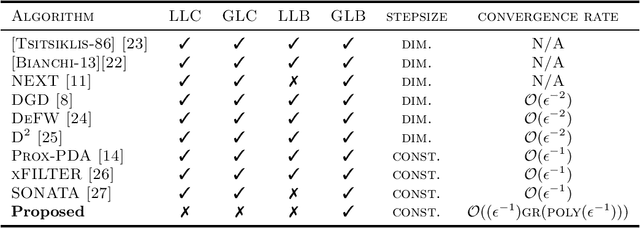
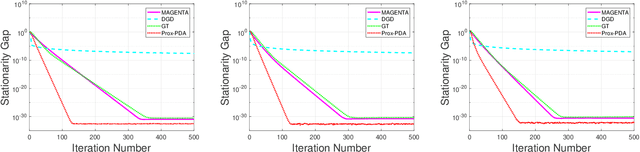
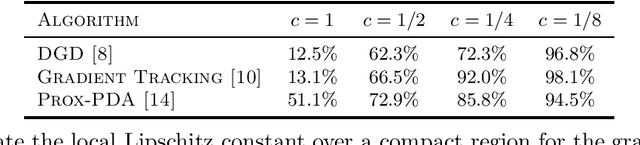
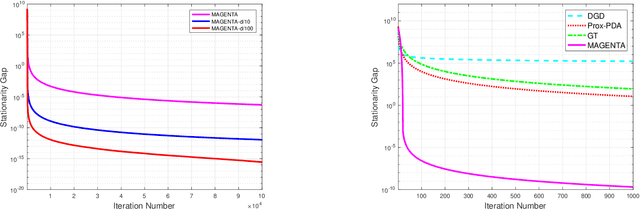
We study a generic class of decentralized algorithms in which $N$ agents jointly optimize the non-convex objective $f(u):=1/N\sum_{i=1}^{N}f_i(u)$, while only communicating with their neighbors. This class of problems has become popular in modeling many signal processing and machine learning applications, and many efficient algorithms have been proposed. However, by constructing some counter-examples, we show that when certain local Lipschitz conditions (LLC) on the local function gradient $\nabla f_i$'s are not satisfied, most of the existing decentralized algorithms diverge, even if the global Lipschitz condition (GLC) is satisfied, where the sum function $f$ has Lipschitz gradient. This observation raises an important open question: How to design decentralized algorithms when the LLC, or even the GLC, is not satisfied? To address the above question, we design a first-order algorithm called Multi-stage gradient tracking algorithm (MAGENTA), which is capable of computing stationary solutions with neither the LLC nor the GLC. In particular, we show that the proposed algorithm converges sublinearly to certain $\epsilon$-stationary solution, where the precise rate depends on various algorithmic and problem parameters. In particular, if the local function $f_i$'s are $Q$th order polynomials, then the rate becomes $\mathcal{O}(1/\epsilon^{Q-1})$. Such a rate is tight for the special case of $Q=2$ where each $f_i$ satisfies LLC. To our knowledge, this is the first attempt that studies decentralized non-convex optimization problems with neither the LLC nor the GLC.

FedPD: A Federated Learning Framework with Optimal Rates and Adaptivity to Non-IID Data

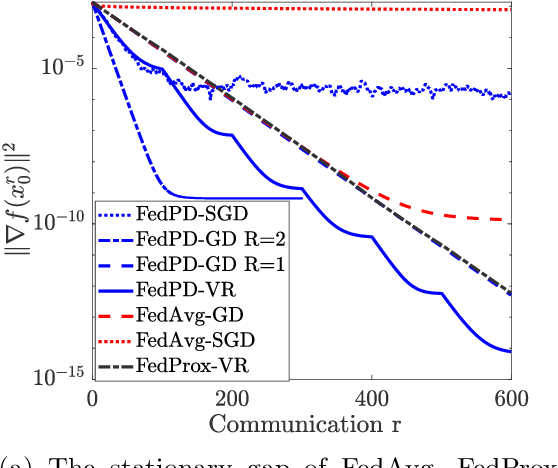
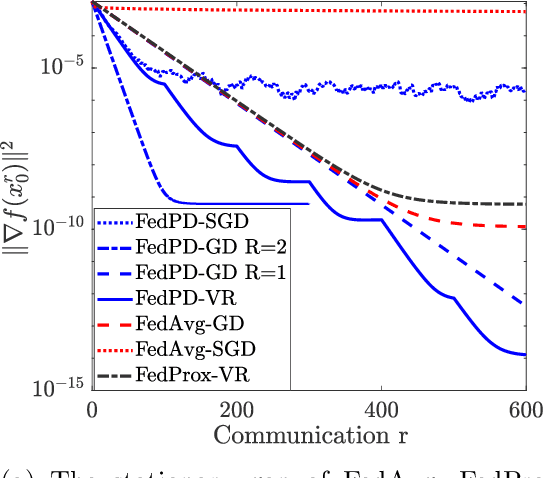
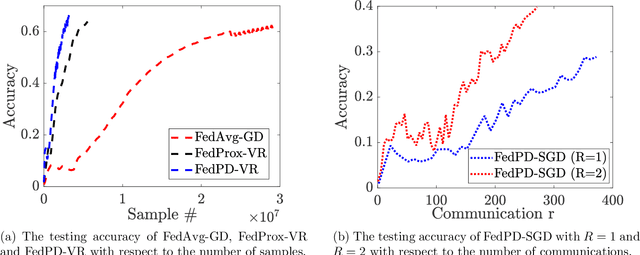
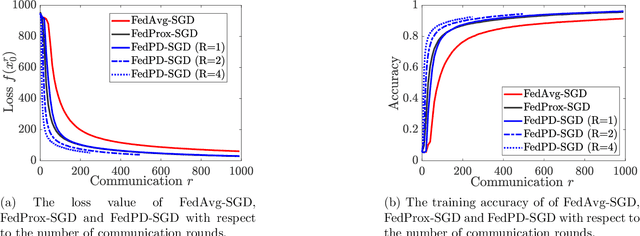
Federated Learning (FL) has become a popular paradigm for learning from distributed data. To effectively utilize data at different devices without moving them to the cloud, algorithms such as the Federated Averaging (FedAvg) have adopted a "computation then aggregation" (CTA) model, in which multiple local updates are performed using local data, before sending the local models to the cloud for aggregation. However, these schemes typically require strong assumptions, such as the local data are identically independent distributed (i.i.d), or the size of the local gradients are bounded. In this paper, we first explicitly characterize the behavior of the FedAvg algorithm, and show that without strong and unrealistic assumptions on the problem structure, the algorithm can behave erratically for non-convex problems (e.g., diverge to infinity). Aiming at designing FL algorithms that are provably fast and require as few assumptions as possible, we propose a new algorithm design strategy from the primal-dual optimization perspective. Our strategy yields a family of algorithms that take the same CTA model as existing algorithms, but they can deal with the non-convex objective, achieve the best possible optimization and communication complexity while being able to deal with both the full batch and mini-batch local computation models. Most importantly, the proposed algorithms are {\it communication efficient}, in the sense that the communication pattern can be adaptive to the level of heterogeneity among the local data. To the best of our knowledge, this is the first algorithmic framework for FL that achieves all the above properties.

Distributed Learning in the Non-Convex World: From Batch to Streaming Data, and Beyond

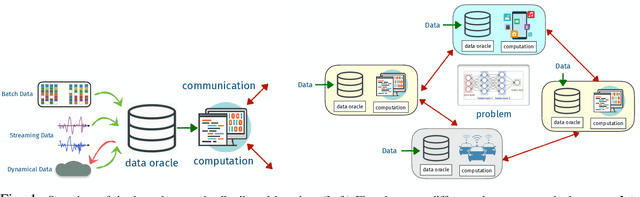
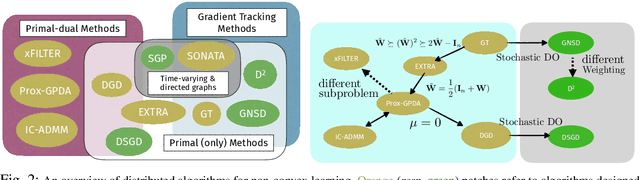
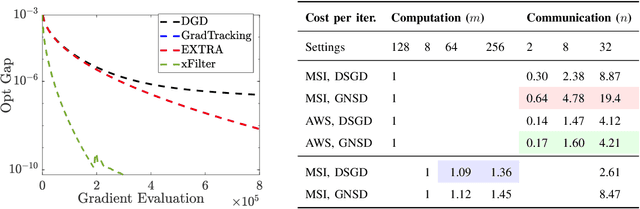
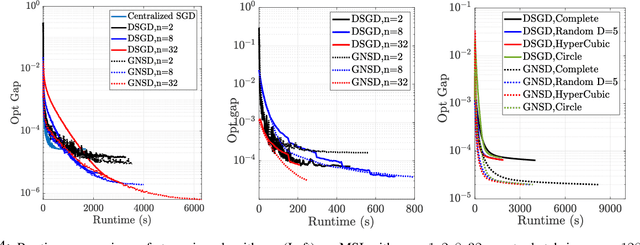
Distributed learning has become a critical enabler of the massively connected world envisioned by many. This article discusses four key elements of scalable distributed processing and real-time intelligence --- problems, data, communication and computation. Our aim is to provide a fresh and unique perspective about how these elements should work together in an effective and coherent manner. In particular, we {provide a selective review} about the recent techniques developed for optimizing non-convex models (i.e., problem classes), processing batch and streaming data (i.e., data types), over the networks in a distributed manner (i.e., communication and computation paradigm). We describe the intuitions and connections behind a core set of popular distributed algorithms, emphasizing how to trade off between computation and communication costs. Practical issues and future research directions will also be discussed.

A Communication Efficient Vertical Federated Learning Framework

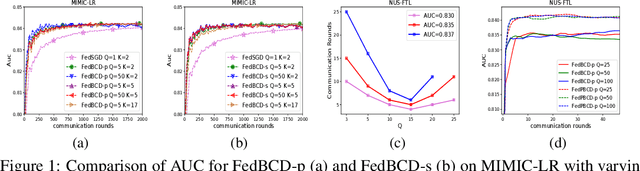
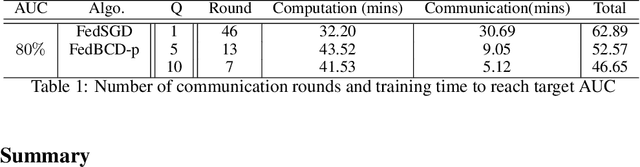
One critical challenge for applying today's Artificial Intelligence (AI) technologies to real-world applications is the common existence of data silos across different organizations. Due to legal, privacy and other practical constraints, data from different organizations cannot be easily integrated. Federated learning (FL), especially the vertical FL (VFL), allows multiple parties having different sets of attributes about the same user collaboratively build models while preserving user privacy. However, communication overhead is a principal bottleneck since the existing VFL protocols require per-iteration communications among all parties. In this paper, we propose the Federated Stochastic Block Coordinate Descent (FedBCD) to effectively reduce the communication rounds for VFL. We show that when the batch size, sample size, and the local iterations are selected appropriately, the algorithm requires $\mathcal{O}(\sqrt{T})$ communication rounds to achieve $\mathcal{O}(1/\sqrt{T})$ accuracy. Finally, we demonstrate the performance of FedBCD on several models and datasets, and on a large-scale industrial platform for VFL.

Dense Recurrent Neural Networks for Inverse Problems: History-Cognizant Unrolling of Optimization Algorithms

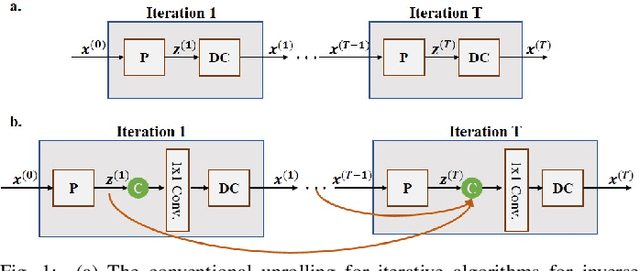
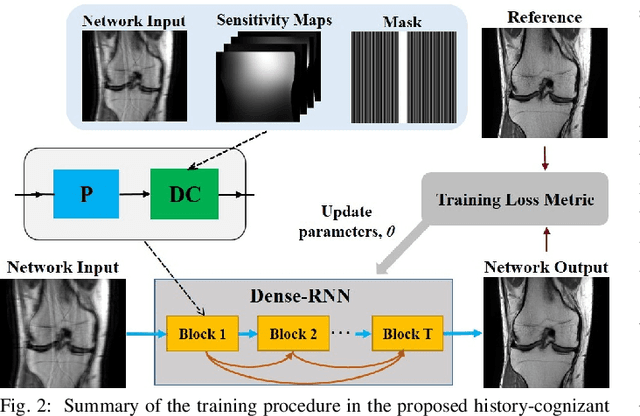
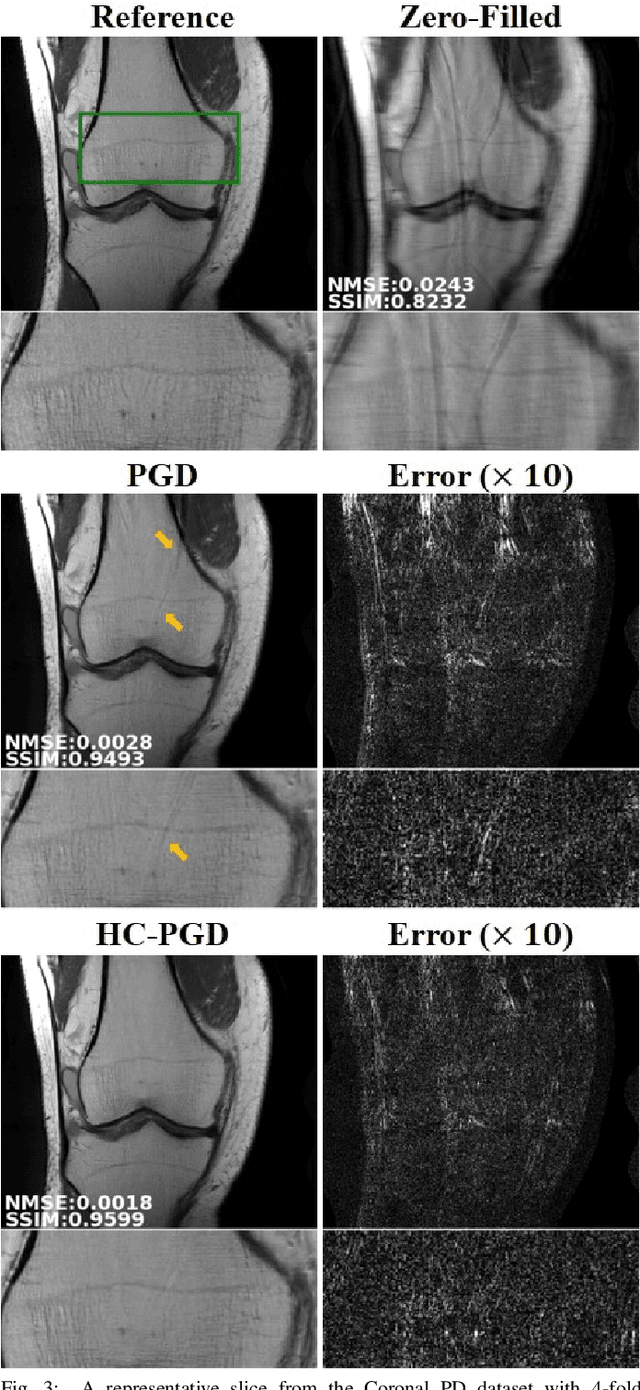
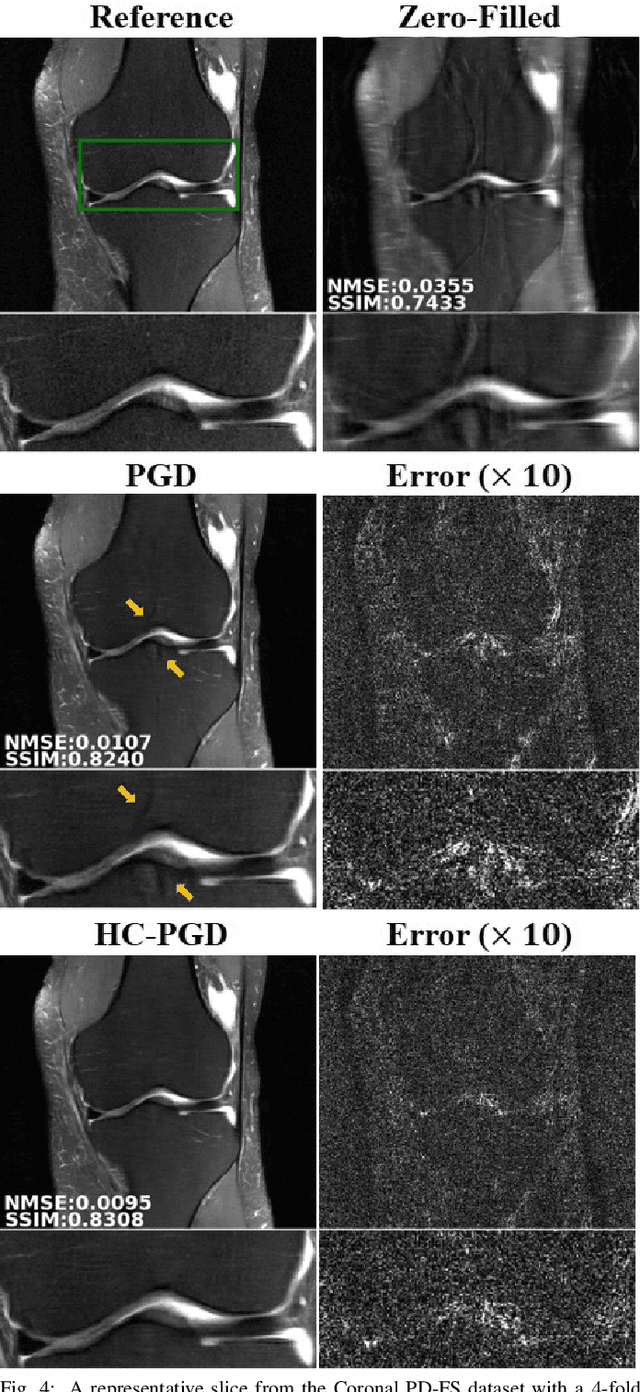
Inverse problems in medical imaging applications incorporate domain-specific knowledge about the forward encoding operator in a regularized reconstruction framework. Recently physics-driven deep learning (DL) methods have been proposed to use neural networks for data-driven regularization. These methods unroll iterative optimization algorithms to solve the inverse problem objective function, by alternating between domain-specific data consistency and data-driven regularization via neural networks. The whole unrolled network is then trained end-to-end to learn the parameters of the network. Due to simplicity of data consistency updates with gradient descent steps, proximal gradient descent (PGD) is a common approach to unroll physics-driven DL reconstruction methods. However, PGD methods have slow convergence rates, necessitating a higher number of unrolled iterations, leading to memory issues in training and slower reconstruction times in testing. Inspired by efficient variants of PGD methods that use a history of the previous iterates, we propose a history-cognizant unrolling of the optimization algorithm with dense connections across iterations for improved performance. In our approach, the gradient descent steps are calculated at a trainable combination of the outputs of all the previous regularization units. We also apply this idea to unrolling variable splitting methods with quadratic relaxation. Our results in reconstruction of the fastMRI knee dataset show that the proposed history-cognizant approach reduces residual aliasing artifacts compared to its conventional unrolled counterpart without requiring extra computational power or increasing reconstruction time.