Towards Better Graph Representation Learning with Parameterized Decomposition & Filtering

Proposing an effective and flexible matrix to represent a graph is a fundamental challenge that has been explored from multiple perspectives, e.g., filtering in Graph Fourier Transforms. In this work, we develop a novel and general framework which unifies many existing GNN models from the view of parameterized decomposition and filtering, and show how it helps to enhance the flexibility of GNNs while alleviating the smoothness and amplification issues of existing models. Essentially, we show that the extensively studied spectral graph convolutions with learnable polynomial filters are constrained variants of this formulation, and releasing these constraints enables our model to express the desired decomposition and filtering simultaneously. Based on this generalized framework, we develop models that are simple in implementation but achieve significant improvements and computational efficiency on a variety of graph learning tasks. Code is available at https://github.com/qslim/PDF.

Soft-mask: Adaptive Substructure Extractions for Graph Neural Networks

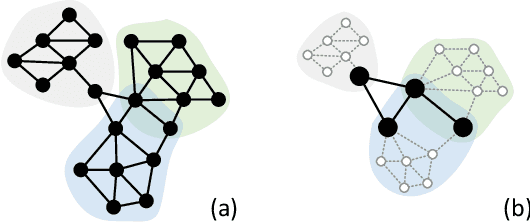
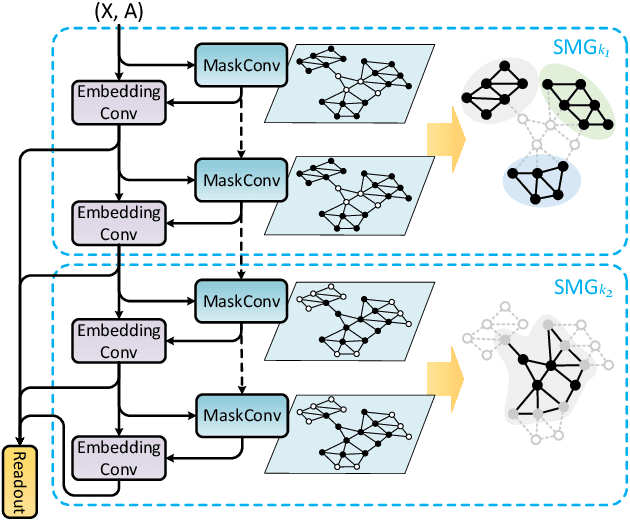
For learning graph representations, not all detailed structures within a graph are relevant to the given graph tasks. Task-relevant structures can be $localized$ or $sparse$ which are only involved in subgraphs or characterized by the interactions of subgraphs (a hierarchical perspective). A graph neural network should be able to efficiently extract task-relevant structures and be invariant to irrelevant parts, which is challenging for general message passing GNNs. In this work, we propose to learn graph representations from a sequence of subgraphs of the original graph to better capture task-relevant substructures or hierarchical structures and skip $noisy$ parts. To this end, we design soft-mask GNN layer to extract desired subgraphs through the mask mechanism. The soft-mask is defined in a continuous space to maintain the differentiability and characterize the weights of different parts. Compared with existing subgraph or hierarchical representation learning methods and graph pooling operations, the soft-mask GNN layer is not limited by the fixed sample or drop ratio, and therefore is more flexible to extract subgraphs with arbitrary sizes. Extensive experiments on public graph benchmarks show that soft-mask mechanism brings performance improvements. And it also provides interpretability where visualizing the values of masks in each layer allows us to have an insight into the structures learned by the model.

Improving Spectral Graph Convolution for Learning Graph-level Representation

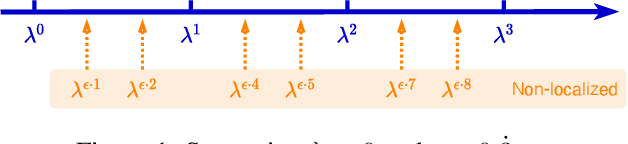
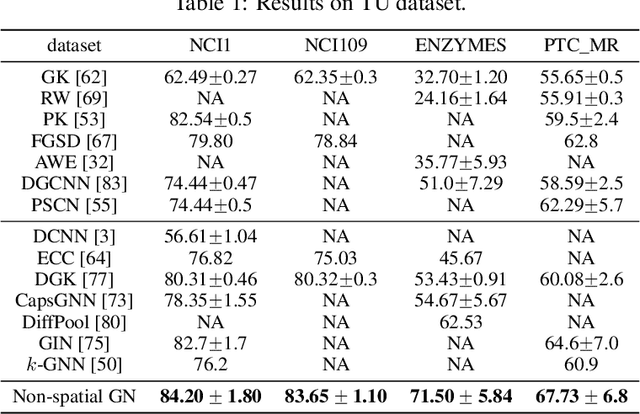
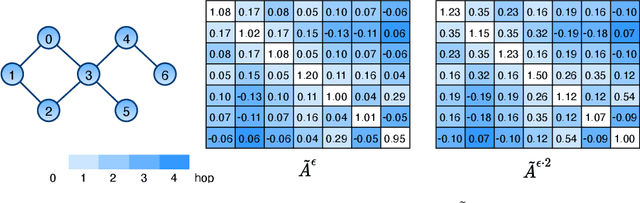
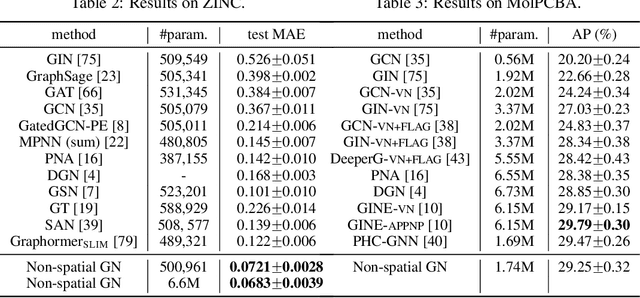
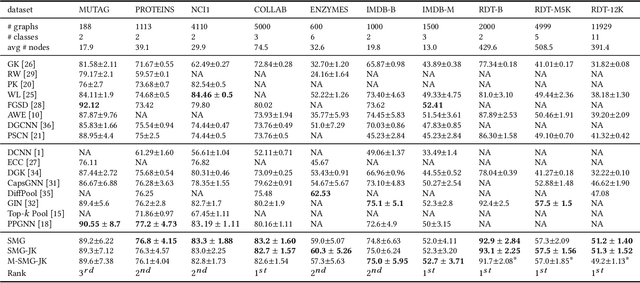
From the original theoretically well-defined spectral graph convolution to the subsequent spatial bassed message-passing model, spatial locality (in vertex domain) acts as a fundamental principle of most graph neural networks (GNNs). In the spectral graph convolution, the filter is approximated by polynomials, where a $k$-order polynomial covers $k$-hop neighbors. In the message-passing, various definitions of neighbors used in aggregations are actually an extensive exploration of the spatial locality information. For learning node representations, the topological distance seems necessary since it characterizes the basic relations between nodes. However, for learning representations of the entire graphs, is it still necessary to hold? In this work, we show that such a principle is not necessary, it hinders most existing GNNs from efficiently encoding graph structures. By removing it, as well as the limitation of polynomial filters, the resulting new architecture significantly boosts performance on learning graph representations. We also study the effects of graph spectrum on signals and interpret various existing improvements as different spectrum smoothing techniques. It serves as a spatial understanding that quantitatively measures the effects of the spectrum to input signals in comparison to the well-known spectral understanding as high/low-pass filters. More importantly, it sheds the light on developing powerful graph representation models.

First Place Solution of KDD Cup 2021 & OGB Large-Scale Challenge Graph Prediction Track

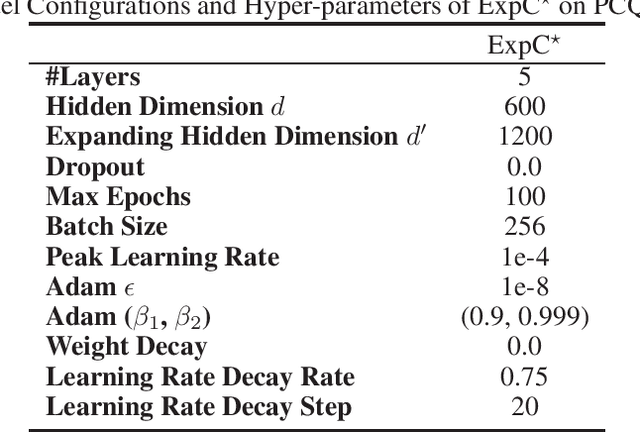
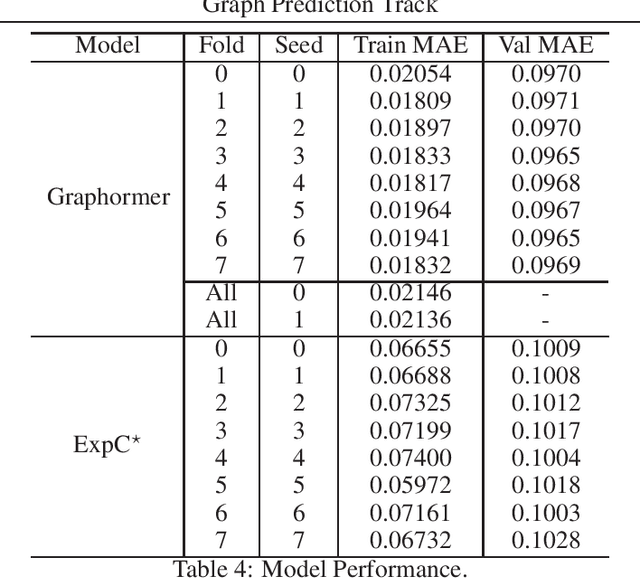
In this technical report, we present our solution of KDD Cup 2021 OGB Large-Scale Challenge - PCQM4M-LSC Track. We adopt Graphormer and ExpC as our basic models. We train each model by 8-fold cross-validation, and additionally train two Graphormer models on the union of training and validation sets with different random seeds. For final submission, we use a naive ensemble for these 18 models by taking average of their outputs. Using our method, our team MachineLearning achieved 0.1200 MAE on test set, which won the first place in KDD Cup graph prediction track.

Breaking the Expressive Bottlenecks of Graph Neural Networks

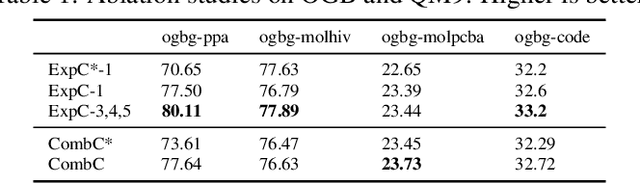
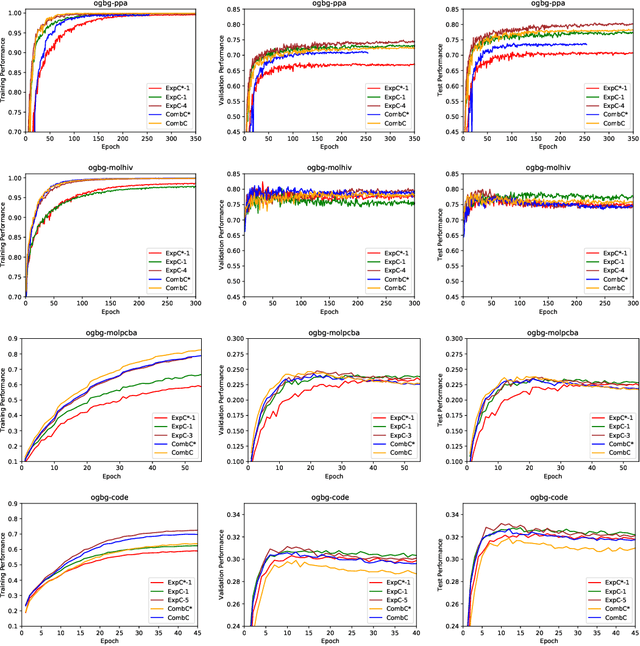
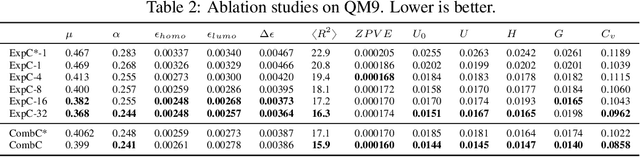
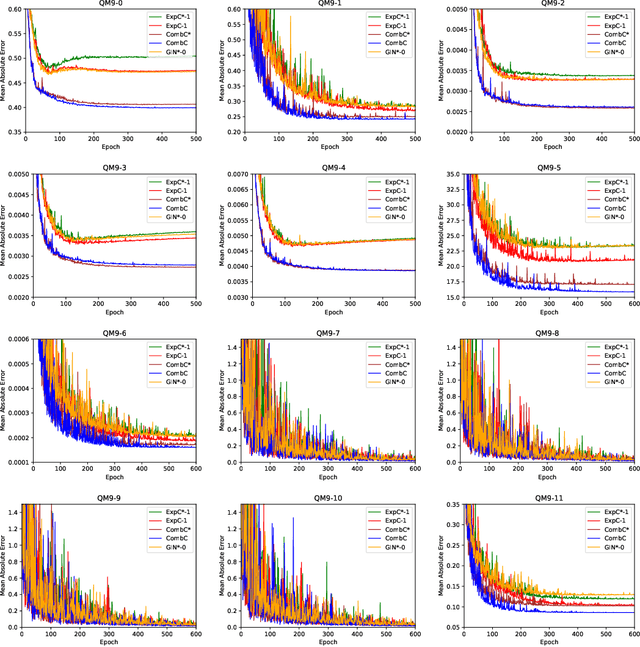
Recently, the Weisfeiler-Lehman (WL) graph isomorphism test was used to measure the expressiveness of graph neural networks (GNNs), showing that the neighborhood aggregation GNNs were at most as powerful as 1-WL test in distinguishing graph structures. There were also improvements proposed in analogy to $k$-WL test ($k>1$). However, the aggregators in these GNNs are far from injective as required by the WL test, and suffer from weak distinguishing strength, making it become expressive bottlenecks. In this paper, we improve the expressiveness by exploring powerful aggregators. We reformulate aggregation with the corresponding aggregation coefficient matrix, and then systematically analyze the requirements of the aggregation coefficient matrix for building more powerful aggregators and even injective aggregators. It can also be viewed as the strategy for preserving the rank of hidden features, and implies that basic aggregators correspond to a special case of low-rank transformations. We also show the necessity of applying nonlinear units ahead of aggregation, which is different from most aggregation-based GNNs. Based on our theoretical analysis, we develop two GNN layers, ExpandingConv and CombConv. Experimental results show that our models significantly boost performance, especially for large and densely connected graphs.