Mixture Weight Estimation and Model Prediction in Multi-source Multi-target Domain Adaptation

We consider the problem of learning a model from multiple heterogeneous sources with the goal of performing well on a new target distribution. The goal of learner is to mix these data sources in a target-distribution aware way and simultaneously minimize the empirical risk on the mixed source. The literature has made some tangible advancements in establishing theory of learning on mixture domain. However, there are still two unsolved problems. Firstly, how to estimate the optimal mixture of sources, given a target domain; Secondly, when there are numerous target domains, how to solve empirical risk minimization (ERM) for each target using possibly unique mixture of data sources in a computationally efficient manner. In this paper we address both problems efficiently and with guarantees. We cast the first problem, mixture weight estimation, as a convex-nonconcave compositional minimax problem, and propose an efficient stochastic algorithm with provable stationarity guarantees. Next, for the second problem, we identify that for certain regimes, solving ERM for each target domain individually can be avoided, and instead parameters for a target optimal model can be viewed as a non-linear function on a space of the mixture coefficients. Building upon this, we show that in the offline setting, a GD-trained overparameterized neural network can provably learn such function to predict the model of target domain instead of solving a designated ERM problem. Finally, we also consider an online setting and propose a label efficient online algorithm, which predicts parameters for new targets given an arbitrary sequence of mixing coefficients, while enjoying regret guarantees.

On the Hardness of Robustness Transfer: A Perspective from Rademacher Complexity over Symmetric Difference Hypothesis Space

Recent studies demonstrated that the adversarially robust learning under $\ell_\infty$ attack is harder to generalize to different domains than standard domain adaptation. How to transfer robustness across different domains has been a key question in domain adaptation field. To investigate the fundamental difficulty behind adversarially robust domain adaptation (or robustness transfer), we propose to analyze a key complexity measure that controls the cross-domain generalization: the adversarial Rademacher complexity over {\em symmetric difference hypothesis space} $\mathcal{H} \Delta \mathcal{H}$. For linear models, we show that adversarial version of this complexity is always greater than the non-adversarial one, which reveals the intrinsic hardness of adversarially robust domain adaptation. We also establish upper bounds on this complexity measure. Then we extend them to the ReLU neural network class by upper bounding the adversarial Rademacher complexity in the binary classification setting. Finally, even though the robust domain adaptation is provably harder, we do find positive relation between robust learning and standard domain adaptation. We explain \emph{how adversarial training helps domain adaptation in terms of standard risk}. We believe our results initiate the study of the generalization theory of adversarially robust domain adaptation, and could shed lights on distributed adversarially robust learning from heterogeneous sources, e.g., federated learning scenario.

Do We Really Need Complicated Model Architectures For Temporal Networks?

Recurrent neural network (RNN) and self-attention mechanism (SAM) are the de facto methods to extract spatial-temporal information for temporal graph learning. Interestingly, we found that although both RNN and SAM could lead to a good performance, in practice neither of them is always necessary. In this paper, we propose GraphMixer, a conceptually and technically simple architecture that consists of three components: (1) a link-encoder that is only based on multi-layer perceptrons (MLP) to summarize the information from temporal links, (2) a node-encoder that is only based on neighbor mean-pooling to summarize node information, and (3) an MLP-based link classifier that performs link prediction based on the outputs of the encoders. Despite its simplicity, GraphMixer attains an outstanding performance on temporal link prediction benchmarks with faster convergence and better generalization performance. These results motivate us to rethink the importance of simpler model architecture.

Efficiently Forgetting What You Have Learned in Graph Representation Learning via Projection

As privacy protection receives much attention, unlearning the effect of a specific node from a pre-trained graph learning model has become equally important. However, due to the node dependency in the graph-structured data, representation unlearning in Graph Neural Networks (GNNs) is challenging and less well explored. In this paper, we fill in this gap by first studying the unlearning problem in linear-GNNs, and then introducing its extension to non-linear structures. Given a set of nodes to unlearn, we propose PROJECTOR that unlearns by projecting the weight parameters of the pre-trained model onto a subspace that is irrelevant to features of the nodes to be forgotten. PROJECTOR could overcome the challenges caused by node dependency and enjoys a perfect data removal, i.e., the unlearned model parameters do not contain any information about the unlearned node features which is guaranteed by algorithmic construction. Empirical results on real-world datasets illustrate the effectiveness and efficiency of PROJECTOR.

Tight Analysis of Extra-gradient and Optimistic Gradient Methods For Nonconvex Minimax Problems

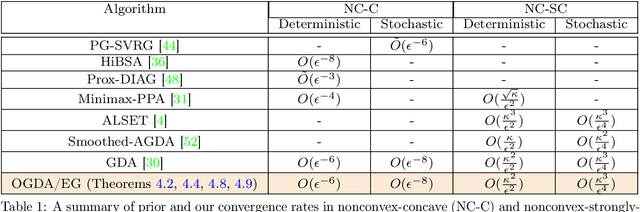
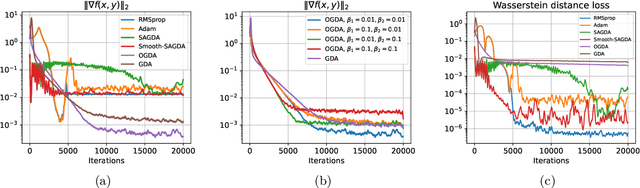
Despite the established convergence theory of Optimistic Gradient Descent Ascent (OGDA) and Extragradient (EG) methods for the convex-concave minimax problems, little is known about the theoretical guarantees of these methods in nonconvex settings. To bridge this gap, for the first time, this paper establishes the convergence of OGDA and EG methods under the nonconvex-strongly-concave (NC-SC) and nonconvex-concave (NC-C) settings by providing a unified analysis through the lens of single-call extra-gradient methods. We further establish lower bounds on the convergence of GDA/OGDA/EG, shedding light on the tightness of our analysis. We also conduct experiments supporting our theoretical results. We believe our results will advance the theoretical understanding of OGDA and EG methods for solving complicated nonconvex minimax real-world problems, e.g., Generative Adversarial Networks (GANs) or robust neural networks training.

Learning Distributionally Robust Models at Scale via Composite Optimization

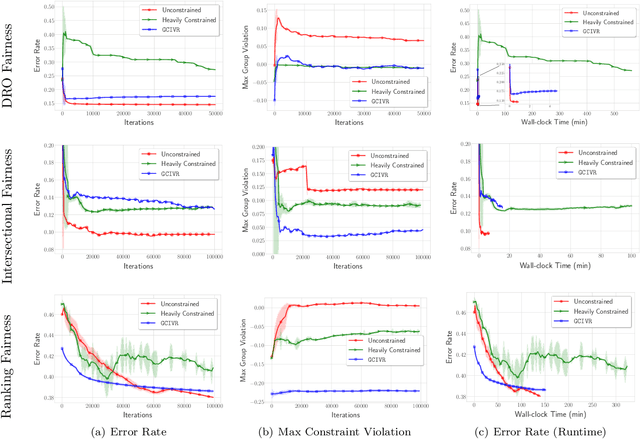
To train machine learning models that are robust to distribution shifts in the data, distributionally robust optimization (DRO) has been proven very effective. However, the existing approaches to learning a distributionally robust model either require solving complex optimization problems such as semidefinite programming or a first-order method whose convergence scales linearly with the number of data samples -- which hinders their scalability to large datasets. In this paper, we show how different variants of DRO are simply instances of a finite-sum composite optimization for which we provide scalable methods. We also provide empirical results that demonstrate the effectiveness of our proposed algorithm with respect to the prior art in order to learn robust models from very large datasets.

Learn Locally, Correct Globally: A Distributed Algorithm for Training Graph Neural Networks

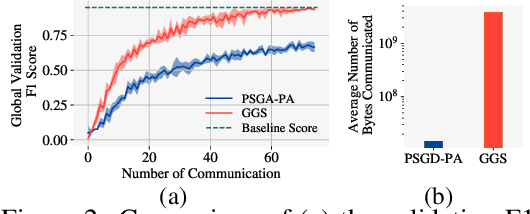
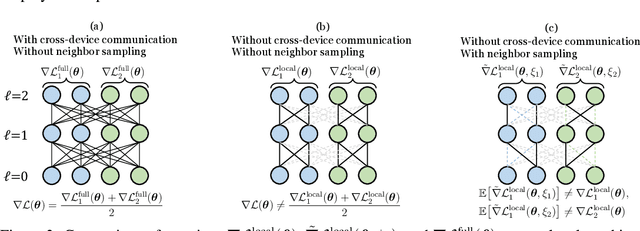
Despite the recent success of Graph Neural Networks (GNNs), training GNNs on large graphs remains challenging. The limited resource capacities of the existing servers, the dependency between nodes in a graph, and the privacy concern due to the centralized storage and model learning have spurred the need to design an effective distributed algorithm for GNN training. However, existing distributed GNN training methods impose either excessive communication costs or large memory overheads that hinders their scalability. To overcome these issues, we propose a communication-efficient distributed GNN training technique named $\text{{Learn Locally, Correct Globally}}$ (LLCG). To reduce the communication and memory overhead, each local machine in LLCG first trains a GNN on its local data by ignoring the dependency between nodes among different machines, then sends the locally trained model to the server for periodic model averaging. However, ignoring node dependency could result in significant performance degradation. To solve the performance degradation, we propose to apply $\text{{Global Server Corrections}}$ on the server to refine the locally learned models. We rigorously analyze the convergence of distributed methods with periodic model averaging for training GNNs and show that naively applying periodic model averaging but ignoring the dependency between nodes will suffer from an irreducible residual error. However, this residual error can be eliminated by utilizing the proposed global corrections to entail fast convergence rate. Extensive experiments on real-world datasets show that LLCG can significantly improve the efficiency without hurting the performance.

Dynamic Graph Representation Learning via Graph Transformer Networks

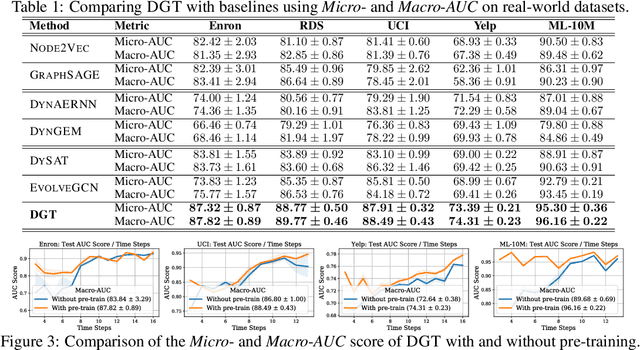
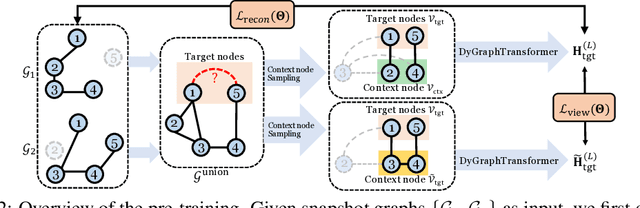
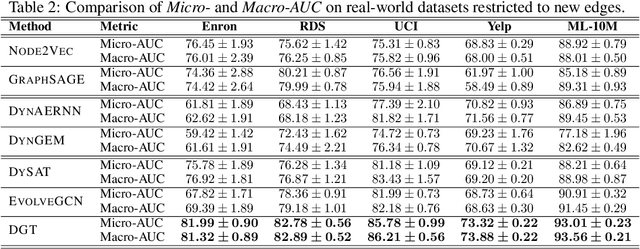
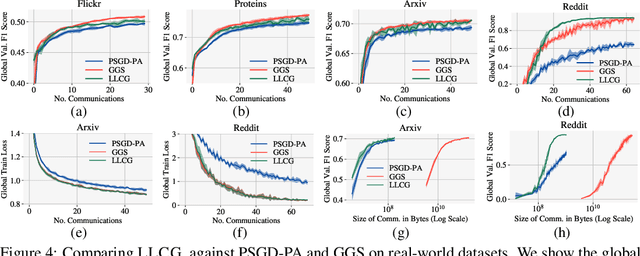
Dynamic graph representation learning is an important task with widespread applications. Previous methods on dynamic graph learning are usually sensitive to noisy graph information such as missing or spurious connections, which can yield degenerated performance and generalization. To overcome this challenge, we propose a Transformer-based dynamic graph learning method named Dynamic Graph Transformer (DGT) with spatial-temporal encoding to effectively learn graph topology and capture implicit links. To improve the generalization ability, we introduce two complementary self-supervised pre-training tasks and show that jointly optimizing the two pre-training tasks results in a smaller Bayesian error rate via an information-theoretic analysis. We also propose a temporal-union graph structure and a target-context node sampling strategy for efficient and scalable training. Extensive experiments on real-world datasets illustrate that DGT presents superior performance compared with several state-of-the-art baselines.

On Provable Benefits of Depth in Training Graph Convolutional Networks

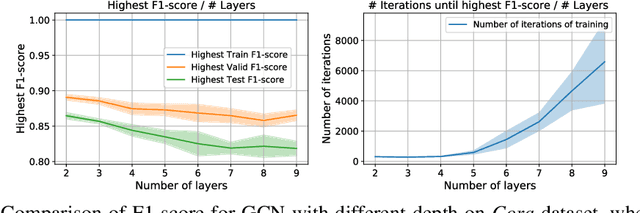
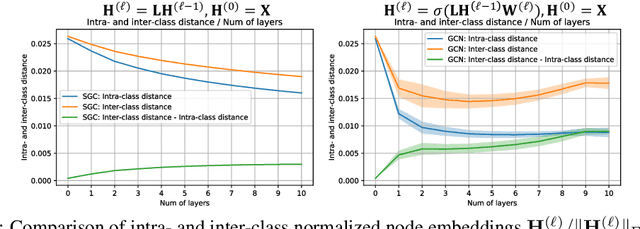
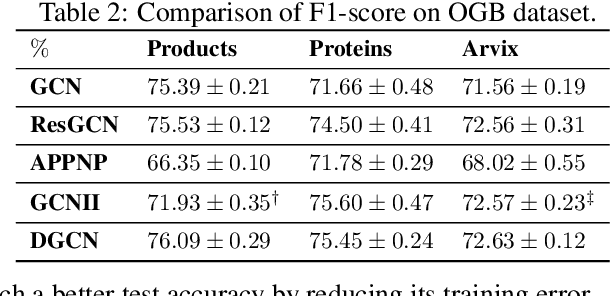
Graph Convolutional Networks (GCNs) are known to suffer from performance degradation as the number of layers increases, which is usually attributed to over-smoothing. Despite the apparent consensus, we observe that there exists a discrepancy between the theoretical understanding of over-smoothing and the practical capabilities of GCNs. Specifically, we argue that over-smoothing does not necessarily happen in practice, a deeper model is provably expressive, can converge to global optimum with linear convergence rate, and achieve very high training accuracy as long as properly trained. Despite being capable of achieving high training accuracy, empirical results show that the deeper models generalize poorly on the testing stage and existing theoretical understanding of such behavior remains elusive. To achieve better understanding, we carefully analyze the generalization capability of GCNs, and show that the training strategies to achieve high training accuracy significantly deteriorate the generalization capability of GCNs. Motivated by these findings, we propose a decoupled structure for GCNs that detaches weight matrices from feature propagation to preserve the expressive power and ensure good generalization performance. We conduct empirical evaluations on various synthetic and real-world datasets to validate the correctness of our theory.

Meta-learning with an Adaptive Task Scheduler

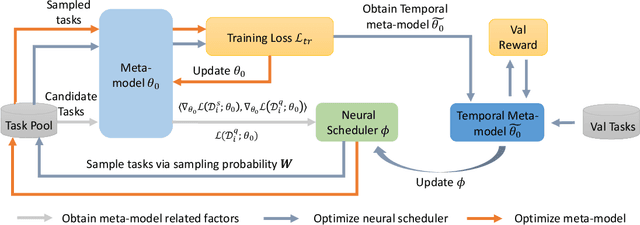
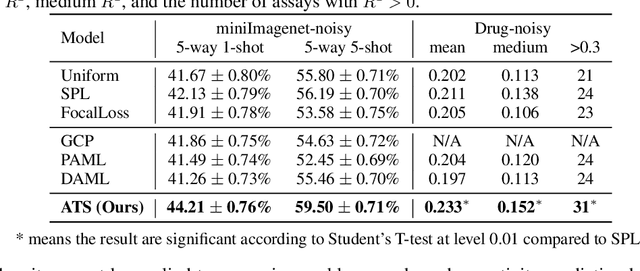
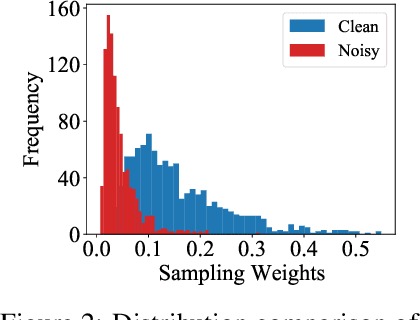
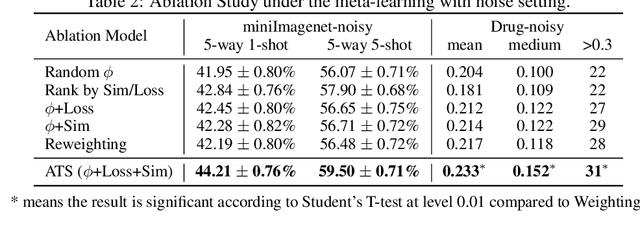
To benefit the learning of a new task, meta-learning has been proposed to transfer a well-generalized meta-model learned from various meta-training tasks. Existing meta-learning algorithms randomly sample meta-training tasks with a uniform probability, under the assumption that tasks are of equal importance. However, it is likely that tasks are detrimental with noise or imbalanced given a limited number of meta-training tasks. To prevent the meta-model from being corrupted by such detrimental tasks or dominated by tasks in the majority, in this paper, we propose an adaptive task scheduler (ATS) for the meta-training process. In ATS, for the first time, we design a neural scheduler to decide which meta-training tasks to use next by predicting the probability being sampled for each candidate task, and train the scheduler to optimize the generalization capacity of the meta-model to unseen tasks. We identify two meta-model-related factors as the input of the neural scheduler, which characterize the difficulty of a candidate task to the meta-model. Theoretically, we show that a scheduler taking the two factors into account improves the meta-training loss and also the optimization landscape. Under the setting of meta-learning with noise and limited budgets, ATS improves the performance on both miniImageNet and a real-world drug discovery benchmark by up to 13% and 18%, respectively, compared to state-of-the-art task schedulers.