CombiGraph-Vis: A Curated Multimodal Olympiad Benchmark for Discrete Mathematical Reasoning

State-of-the-art (SOTA) LLMs have progressed from struggling on proof-based Olympiad problems to solving most of the IMO 2025 problems, with leading systems reportedly handling 5 of 6 problems. Given this progress, we assess how well these models can grade proofs: detecting errors, judging their severity, and assigning fair scores beyond binary correctness. We study proof-analysis capabilities using a corpus of 90 Gemini 2.5 Pro-generated solutions that we grade on a 1-4 scale with detailed error annotations, and on MathArena solution sets for IMO/USAMO 2025 scored on a 0-7 scale. Our analysis shows that models can reliably flag incorrect (including subtly incorrect) solutions but exhibit calibration gaps in how partial credit is assigned. To address this, we introduce agentic workflows that extract and analyze reference solutions and automatically derive problem-specific rubrics for a multi-step grading process. We instantiate and compare different design choices for the grading workflows, and evaluate their trade-offs. Across our annotated corpus and MathArena, our proposed workflows achieve higher agreement with human grades and more consistent handling of partial credit across metrics. We release all code, data, and prompts/logs to facilitate future research.

Distributed Personalized Empirical Risk Minimization

This paper advocates a new paradigm Personalized Empirical Risk Minimization (PERM) to facilitate learning from heterogeneous data sources without imposing stringent constraints on computational resources shared by participating devices. In PERM, we aim to learn a distinct model for each client by learning who to learn with and personalizing the aggregation of local empirical losses by effectively estimating the statistical discrepancy among data distributions, which entails optimal statistical accuracy for all local distributions and overcomes the data heterogeneity issue. To learn personalized models at scale, we propose a distributed algorithm that replaces the standard model averaging with model shuffling to simultaneously optimize PERM objectives for all devices. This also allows us to learn distinct model architectures (e.g., neural networks with different numbers of parameters) for different clients, thus confining underlying memory and compute resources of individual clients. We rigorously analyze the convergence of the proposed algorithm and conduct experiments that corroborate the effectiveness of the proposed paradigm.

Tight Analysis of Extra-gradient and Optimistic Gradient Methods For Nonconvex Minimax Problems

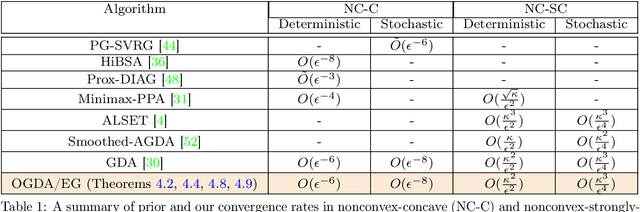
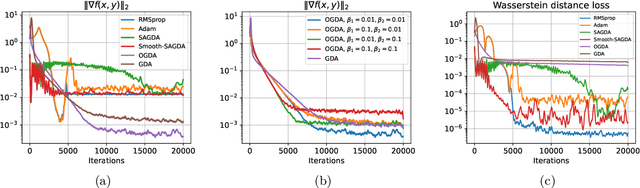
Despite the established convergence theory of Optimistic Gradient Descent Ascent (OGDA) and Extragradient (EG) methods for the convex-concave minimax problems, little is known about the theoretical guarantees of these methods in nonconvex settings. To bridge this gap, for the first time, this paper establishes the convergence of OGDA and EG methods under the nonconvex-strongly-concave (NC-SC) and nonconvex-concave (NC-C) settings by providing a unified analysis through the lens of single-call extra-gradient methods. We further establish lower bounds on the convergence of GDA/OGDA/EG, shedding light on the tightness of our analysis. We also conduct experiments supporting our theoretical results. We believe our results will advance the theoretical understanding of OGDA and EG methods for solving complicated nonconvex minimax real-world problems, e.g., Generative Adversarial Networks (GANs) or robust neural networks training.