SILMM: Self-Improving Large Multimodal Models for Compositional Text-to-Image Generation

Large Multimodal Models (LMMs) have demonstrated impressive capabilities in multimodal understanding and generation, pushing forward advancements in text-to-image generation. However, achieving accurate text-image alignment for LMMs, particularly in compositional scenarios, remains challenging. Existing approaches, such as layout planning for multi-step generation and learning from human feedback or AI feedback, depend heavily on prompt engineering, costly human annotations, and continual upgrading, limiting flexibility and scalability. In this work, we introduce a model-agnostic iterative self-improvement framework (SILMM) that can enable LMMs to provide helpful and scalable self-feedback and optimize text-image alignment via Direct Preference Optimization (DPO). DPO can readily applied to LMMs that use discrete visual tokens as intermediate image representations; while it is less suitable for LMMs with continuous visual features, as obtaining generation probabilities is challenging. To adapt SILMM to LMMs with continuous features, we propose a diversity mechanism to obtain diverse representations and a kernel-based continuous DPO for alignment. Extensive experiments on three compositional text-to-image generation benchmarks validate the effectiveness and superiority of SILMM, showing improvements exceeding 30% on T2I-CompBench++ and around 20% on DPG-Bench.

Unified Text-to-Image Generation and Retrieval

How humans can efficiently and effectively acquire images has always been a perennial question. A typical solution is text-to-image retrieval from an existing database given the text query; however, the limited database typically lacks creativity. By contrast, recent breakthroughs in text-to-image generation have made it possible to produce fancy and diverse visual content, but it faces challenges in synthesizing knowledge-intensive images. In this work, we rethink the relationship between text-to-image generation and retrieval and propose a unified framework in the context of Multimodal Large Language Models (MLLMs). Specifically, we first explore the intrinsic discriminative abilities of MLLMs and introduce a generative retrieval method to perform retrieval in a training-free manner. Subsequently, we unify generation and retrieval in an autoregressive generation way and propose an autonomous decision module to choose the best-matched one between generated and retrieved images as the response to the text query. Additionally, we construct a benchmark called TIGeR-Bench, including creative and knowledge-intensive domains, to standardize the evaluation of unified text-to-image generation and retrieval. Extensive experimental results on TIGeR-Bench and two retrieval benchmarks, i.e., Flickr30K and MS-COCO, demonstrate the superiority and effectiveness of our proposed method.

Convex and Non-Convex Optimization under Generalized Smoothness

Classical analysis of convex and non-convex optimization methods often requires the Lipshitzness of the gradient, which limits the analysis to functions bounded by quadratics. Recent work relaxed this requirement to a non-uniform smoothness condition with the Hessian norm bounded by an affine function of the gradient norm, and proved convergence in the non-convex setting via gradient clipping, assuming bounded noise. In this paper, we further generalize this non-uniform smoothness condition and develop a simple, yet powerful analysis technique that bounds the gradients along the trajectory, thereby leading to stronger results for both convex and non-convex optimization problems. In particular, we obtain the classical convergence rates for (stochastic) gradient descent and Nesterov's accelerated gradient method in the convex and/or non-convex setting under this general smoothness condition. The new analysis approach does not require gradient clipping and allows heavy-tailed noise with bounded variance in the stochastic setting.

Convergence of Adam Under Relaxed Assumptions

In this paper, we provide a rigorous proof of convergence of the Adaptive Moment Estimate (Adam) algorithm for a wide class of optimization objectives. Despite the popularity and efficiency of the Adam algorithm in training deep neural networks, its theoretical properties are not yet fully understood, and existing convergence proofs require unrealistically strong assumptions, such as globally bounded gradients, to show the convergence to stationary points. In this paper, we show that Adam provably converges to $\epsilon$-stationary points with $\mathcal{O}(\epsilon^{-4})$ gradient complexity under far more realistic conditions. The key to our analysis is a new proof of boundedness of gradients along the optimization trajectory, under a generalized smoothness assumption according to which the local smoothness (i.e., Hessian norm when it exists) is bounded by a sub-quadratic function of the gradient norm. Moreover, we propose a variance-reduced version of Adam with an accelerated gradient complexity of $\mathcal{O}(\epsilon^{-3})$.

Variance-reduced Clipping for Non-convex Optimization

Gradient clipping is a standard training technique used in deep learning applications such as large-scale language modeling to mitigate exploding gradients. Recent experimental studies have demonstrated a fairly special behavior in the smoothness of the training objective along its trajectory when trained with gradient clipping. That is, the smoothness grows with the gradient norm. This is in clear contrast to the well-established assumption in folklore non-convex optimization, a.k.a. $L$-smoothness, where the smoothness is assumed to be bounded by a constant $L$ globally. The recently introduced $(L_0,L_1)$-smoothness is a more relaxed notion that captures such behavior in non-convex optimization. In particular, it has been shown that under this relaxed smoothness assumption, SGD with clipping requires $O(\epsilon^{-4})$ stochastic gradient computations to find an $\epsilon$-stationary solution. In this paper, we employ a variance reduction technique, namely SPIDER, and demonstrate that for a carefully designed learning rate, this complexity is improved to $O(\epsilon^{-3})$ which is order-optimal. The corresponding learning rate comprises the clipping technique to mitigate the growing smoothness. Moreover, when the objective function is the average of $n$ components, we improve the existing $O(n\epsilon^{-2})$ bound on the stochastic gradient complexity to order-optimal $O(\sqrt{n} \epsilon^{-2} + n)$.

Tight Analysis of Extra-gradient and Optimistic Gradient Methods For Nonconvex Minimax Problems

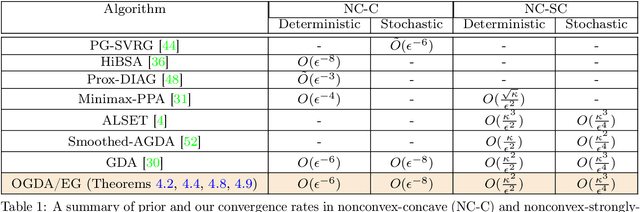
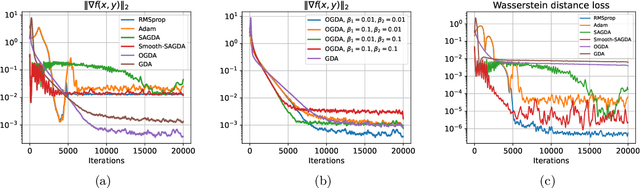
Despite the established convergence theory of Optimistic Gradient Descent Ascent (OGDA) and Extragradient (EG) methods for the convex-concave minimax problems, little is known about the theoretical guarantees of these methods in nonconvex settings. To bridge this gap, for the first time, this paper establishes the convergence of OGDA and EG methods under the nonconvex-strongly-concave (NC-SC) and nonconvex-concave (NC-C) settings by providing a unified analysis through the lens of single-call extra-gradient methods. We further establish lower bounds on the convergence of GDA/OGDA/EG, shedding light on the tightness of our analysis. We also conduct experiments supporting our theoretical results. We believe our results will advance the theoretical understanding of OGDA and EG methods for solving complicated nonconvex minimax real-world problems, e.g., Generative Adversarial Networks (GANs) or robust neural networks training.

On Convergence of Gradient Descent Ascent: A Tight Local Analysis

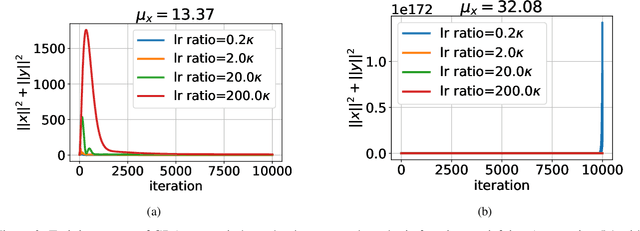
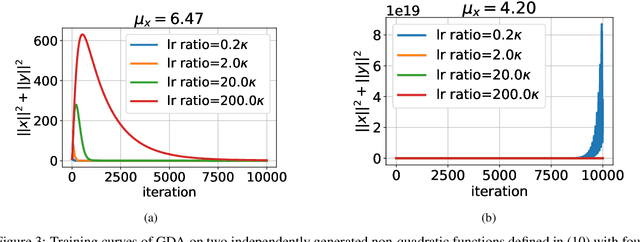
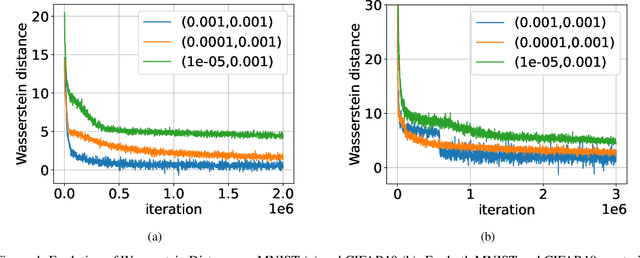
Gradient Descent Ascent (GDA) methods are the mainstream algorithms for minimax optimization in generative adversarial networks (GANs). Convergence properties of GDA have drawn significant interest in the recent literature. Specifically, for $\min_{\mathbf{x}} \max_{\mathbf{y}} f(\mathbf{x};\mathbf{y})$ where $f$ is strongly-concave in $\mathbf{y}$ and possibly nonconvex in $\mathbf{x}$, (Lin et al., 2020) proved the convergence of GDA with a stepsize ratio $\eta_{\mathbf{y}}/\eta_{\mathbf{x}}=\Theta(\kappa^2)$ where $\eta_{\mathbf{x}}$ and $\eta_{\mathbf{y}}$ are the stepsizes for $\mathbf{x}$ and $\mathbf{y}$ and $\kappa$ is the condition number for $\mathbf{y}$. While this stepsize ratio suggests a slow training of the min player, practical GAN algorithms typically adopt similar stepsizes for both variables, indicating a wide gap between theoretical and empirical results. In this paper, we aim to bridge this gap by analyzing the \emph{local convergence} of general \emph{nonconvex-nonconcave} minimax problems. We demonstrate that a stepsize ratio of $\Theta(\kappa)$ is necessary and sufficient for local convergence of GDA to a Stackelberg Equilibrium, where $\kappa$ is the local condition number for $\mathbf{y}$. We prove a nearly tight convergence rate with a matching lower bound. We further extend the convergence guarantees to stochastic GDA and extra-gradient methods (EG). Finally, we conduct several numerical experiments to support our theoretical findings.

Byzantine-Robust Federated Linear Bandits

In this paper, we study a linear bandit optimization problem in a federated setting where a large collection of distributed agents collaboratively learn a common linear bandit model. Standard federated learning algorithms applied to this setting are vulnerable to Byzantine attacks on even a small fraction of agents. We propose a novel algorithm with a robust aggregation oracle that utilizes the geometric median. We prove that our proposed algorithm is robust to Byzantine attacks on fewer than half of agents and achieves a sublinear $\tilde{\mathcal{O}}({T^{3/4}})$ regret with $\mathcal{O}(\sqrt{T})$ steps of communication in $T$ steps. Moreover, we make our algorithm differentially private via a tree-based mechanism. Finally, if the level of corruption is known to be small, we show that using the geometric median of mean oracle for robust aggregation further improves the regret bound.

On Convergence of Training Loss Without Reaching Stationary Points

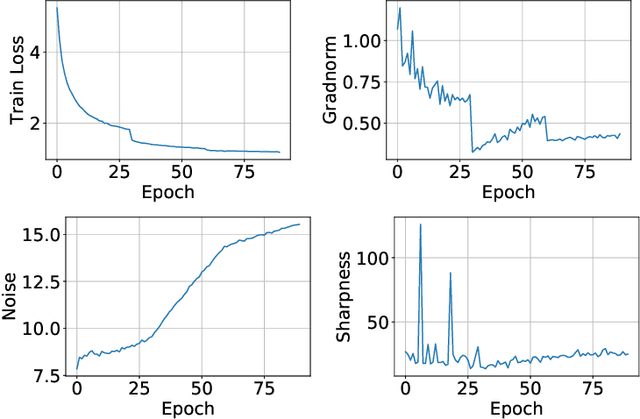
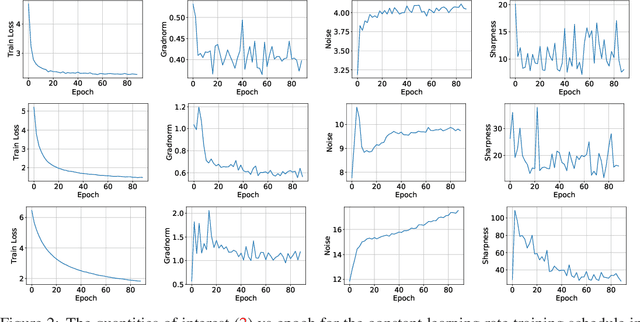
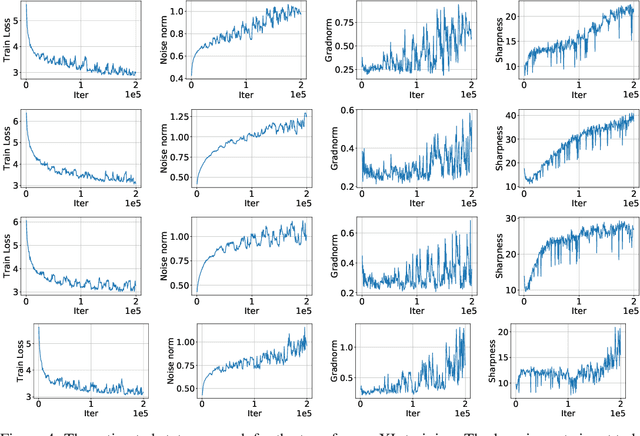
It is a well-known fact that nonconvex optimization is computationally intractable in the worst case. As a result, theoretical analysis of optimization algorithms such as gradient descent often focuses on local convergence to stationary points where the gradient norm is zero or negligible. In this work, we examine the disconnect between the existing theoretical analysis of gradient-based algorithms and actual practice. Specifically, we provide numerical evidence that in large-scale neural network training, such as in ImageNet, ResNet, and WT103 + TransformerXL models, the Neural Network weight variables do not converge to stationary points where the gradient of the loss function vanishes. Remarkably, however, we observe that while weights do not converge to stationary points, the value of the loss function converges. Inspired by this observation, we propose a new perspective based on ergodic theory of dynamical systems. We prove convergence of the distribution of weight values to an approximate invariant measure (without smoothness assumptions) that explains this phenomenon. We further discuss how this perspective can better align the theory with empirical observations.

Complexity Lower Bounds for Nonconvex-Strongly-Concave Min-Max Optimization

We provide a first-order oracle complexity lower bound for finding stationary points of min-max optimization problems where the objective function is smooth, nonconvex in the minimization variable, and strongly concave in the maximization variable. We establish a lower bound of $\Omega\left(\sqrt{\kappa}\epsilon^{-2}\right)$ for deterministic oracles, where $\epsilon$ defines the level of approximate stationarity and $\kappa$ is the condition number. Our analysis shows that the upper bound achieved in (Lin et al., 2020b) is optimal in the $\epsilon$ and $\kappa$ dependence up to logarithmic factors. For stochastic oracles, we provide a lower bound of $\Omega\left(\sqrt{\kappa}\epsilon^{-2} + \kappa^{1/3}\epsilon^{-4}\right)$. It suggests that there is a significant gap between the upper bound $\mathcal{O}(\kappa^3 \epsilon^{-4})$ in (Lin et al., 2020a) and our lower bound in the condition number dependence.