Towards Infinitely Long Neural Simulations: Self-Refining Neural Surrogate Models for Dynamical Systems

Recent advances in autoregressive neural surrogate models have enabled orders-of-magnitude speedups in simulating dynamical systems. However, autoregressive models are generally prone to distribution drift: compounding errors in autoregressive rollouts that severely degrade generation quality over long time horizons. Existing work attempts to address this issue by implicitly leveraging the inherent trade-off between short-time accuracy and long-time consistency through hyperparameter tuning. In this work, we introduce a unifying mathematical framework that makes this tradeoff explicit, formalizing and generalizing hyperparameter-based strategies in existing approaches. Within this framework, we propose a robust, hyperparameter-free model implemented as a conditional diffusion model that balances short-time fidelity with long-time consistency by construction. Our model, Self-refining Neural Surrogate model (SNS), can be implemented as a standalone model that refines its own autoregressive outputs or as a complementary model to existing neural surrogates to ensure long-time consistency. We also demonstrate the numerical feasibility of SNS through high-fidelity simulations of complex dynamical systems over arbitrarily long time horizons.

Generative Modeling from Black-box Corruptions via Self-Consistent Stochastic Interpolants

Transport-based methods have emerged as a leading paradigm for building generative models from large, clean datasets. However, in many scientific and engineering domains, clean data are often unavailable: instead, we only observe measurements corrupted through a noisy, ill-conditioned channel. A generative model for the original data thus requires solving an inverse problem at the level of distributions. In this work, we introduce a novel approach to this task based on Stochastic Interpolants: we iteratively update a transport map between corrupted and clean data samples using only access to the corrupted dataset as well as black box access to the corruption channel. Under appropriate conditions, this iterative procedure converges towards a self-consistent transport map that effectively inverts the corruption channel, thus enabling a generative model for the clean data. We refer to the resulting method as the self-consistent stochastic interpolant (SCSI). It (i) is computationally efficient compared to variational alternatives, (ii) highly flexible, handling arbitrary nonlinear forward models with only black-box access, and (iii) enjoys theoretical guarantees. We demonstrate superior performance on inverse problems in natural image processing and scientific reconstruction, and establish convergence guarantees of the scheme under appropriate assumptions.

The Generative Leap: Sharp Sample Complexity for Efficiently Learning Gaussian Multi-Index Models

In this work we consider generic Gaussian Multi-index models, in which the labels only depend on the (Gaussian) $d$-dimensional inputs through their projection onto a low-dimensional $r = O_d(1)$ subspace, and we study efficient agnostic estimation procedures for this hidden subspace. We introduce the \emph{generative leap} exponent $k^\star$, a natural extension of the generative exponent from [Damian et al.'24] to the multi-index setting. We first show that a sample complexity of $n=\Theta(d^{1 \vee \k/2})$ is necessary in the class of algorithms captured by the Low-Degree-Polynomial framework. We then establish that this sample complexity is also sufficient, by giving an agnostic sequential estimation procedure (that is, requiring no prior knowledge of the multi-index model) based on a spectral U-statistic over appropriate Hermite tensors. We further compute the generative leap exponent for several examples including piecewise linear functions (deep ReLU networks with bias), and general deep neural networks (with $r$-dimensional first hidden layer).

Propagation of Chaos in One-hidden-layer Neural Networks beyond Logarithmic Time

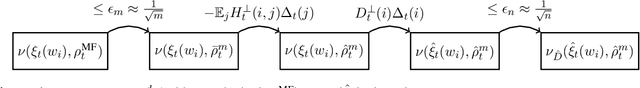
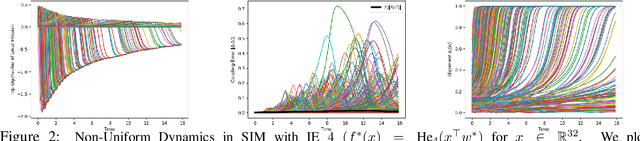
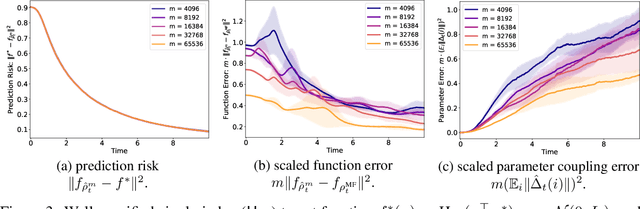
We study the approximation gap between the dynamics of a polynomial-width neural network and its infinite-width counterpart, both trained using projected gradient descent in the mean-field scaling regime. We demonstrate how to tightly bound this approximation gap through a differential equation governed by the mean-field dynamics. A key factor influencing the growth of this ODE is the local Hessian of each particle, defined as the derivative of the particle's velocity in the mean-field dynamics with respect to its position. We apply our results to the canonical feature learning problem of estimating a well-specified single-index model; we permit the information exponent to be arbitrarily large, leading to convergence times that grow polynomially in the ambient dimension $d$. We show that, due to a certain ``self-concordance'' property in these problems -- where the local Hessian of a particle is bounded by a constant times the particle's velocity -- polynomially many neurons are sufficient to closely approximate the mean-field dynamics throughout training.

Survey on Algorithms for multi-index models

We review the literature on algorithms for estimating the index space in a multi-index model. The primary focus is on computationally efficient (polynomial-time) algorithms in Gaussian space, the assumptions under which consistency is guaranteed by these methods, and their sample complexity. In many cases, a gap is observed between the sample complexity of the best known computationally efficient methods and the information-theoretical minimum. We also review algorithms based on estimating the span of gradients using nonparametric methods, and algorithms based on fitting neural networks using gradient descent

Thermalizer: Stable autoregressive neural emulation of spatiotemporal chaos

Autoregressive surrogate models (or \textit{emulators}) of spatiotemporal systems provide an avenue for fast, approximate predictions, with broad applications across science and engineering. At inference time, however, these models are generally unable to provide predictions over long time rollouts due to accumulation of errors leading to diverging trajectories. In essence, emulators operate out of distribution, and controlling the online distribution quickly becomes intractable in large-scale settings. To address this fundamental issue, and focusing on time-stationary systems admitting an invariant measure, we leverage diffusion models to obtain an implicit estimator of the score of this invariant measure. We show that this model of the score function can be used to stabilize autoregressive emulator rollouts by applying on-the-fly denoising during inference, a process we call \textit{thermalization}. Thermalizing an emulator rollout is shown to extend the time horizon of stable predictions by an order of magnitude in complex systems exhibiting turbulent and chaotic behavior, opening up a novel application of diffusion models in the context of neural emulation.

Compositional Reasoning with Transformers, RNNs, and Chain of Thought

We study and compare the expressive power of transformers, RNNs, and transformers with chain of thought tokens on a simple and natural class of problems we term Compositional Reasoning Questions (CRQ). This family captures problems like evaluating Boolean formulas and multi-step word problems. Assuming standard hardness assumptions from circuit complexity and communication complexity, we prove that none of these three architectures is capable of solving CRQs unless some hyperparameter (depth, embedding dimension, and number of chain of thought tokens, respectively) grows with the size of the input. We also provide a construction for each architecture that solves CRQs. For transformers, our construction uses depth that is logarithmic in the problem size. For RNNs, logarithmic embedding dimension is necessary and sufficient, so long as the inputs are provided in a certain order. (Otherwise, a linear dimension is necessary). For transformers with chain of thought, our construction uses $n$ CoT tokens. These results show that, while CRQs are inherently hard, there are several different ways for language models to overcome this hardness. Even for a single class of problems, each architecture has strengths and weaknesses, and none is strictly better than the others.

Geometry and Optimization of Shallow Polynomial Networks

We study shallow neural networks with polynomial activations. The function space for these models can be identified with a set of symmetric tensors with bounded rank. We describe general features of these networks, focusing on the relationship between width and optimization. We then consider teacher-student problems, that can be viewed as a problem of low-rank tensor approximation with respect to a non-standard inner product that is induced by the data distribution. In this setting, we introduce a teacher-metric discriminant which encodes the qualitative behavior of the optimization as a function of the training data distribution. Finally, we focus on networks with quadratic activations, presenting an in-depth analysis of the optimization landscape. In particular, we present a variation of the Eckart-Young Theorem characterizing all critical points and their Hessian signatures for teacher-student problems with quadratic networks and Gaussian training data.

On the Benefits of Rank in Attention Layers

Attention-based mechanisms are widely used in machine learning, most prominently in transformers. However, hyperparameters such as the rank of the attention matrices and the number of heads are scaled nearly the same way in all realizations of this architecture, without theoretical justification. In this work we show that there are dramatic trade-offs between the rank and number of heads of the attention mechanism. Specifically, we present a simple and natural target function that can be represented using a single full-rank attention head for any context length, but that cannot be approximated by low-rank attention unless the number of heads is exponential in the embedding dimension, even for short context lengths. Moreover, we prove that, for short context lengths, adding depth allows the target to be approximated by low-rank attention. For long contexts, we conjecture that full-rank attention is necessary. Finally, we present experiments with off-the-shelf transformers that validate our theoretical findings.

Posterior Sampling with Denoising Oracles via Tilted Transport

Score-based diffusion models have significantly advanced high-dimensional data generation across various domains, by learning a denoising oracle (or score) from datasets. From a Bayesian perspective, they offer a realistic modeling of data priors and facilitate solving inverse problems through posterior sampling. Although many heuristic methods have been developed recently for this purpose, they lack the quantitative guarantees needed in many scientific applications. In this work, we introduce the \textit{tilted transport} technique, which leverages the quadratic structure of the log-likelihood in linear inverse problems in combination with the prior denoising oracle to transform the original posterior sampling problem into a new `boosted' posterior that is provably easier to sample from. We quantify the conditions under which this boosted posterior is strongly log-concave, highlighting the dependencies on the condition number of the measurement matrix and the signal-to-noise ratio. The resulting posterior sampling scheme is shown to reach the computational threshold predicted for sampling Ising models [Kunisky'23] with a direct analysis, and is further validated on high-dimensional Gaussian mixture models and scalar field $\varphi^4$ models.