Critical Points of Degenerate Metrics on Algebraic Varieties: A Tale of Overparametrization

We study the critical points over an algebraic variety of an optimization problem defined by a quadratic objective that is degenerate. This scenario arises in machine learning when the dataset size is small with respect to the model, and is typically referred to as overparametrization. Our main result relates the degenerate optimization problem to a nondegenerate one via a projection. In the highly-degenerate regime, we find that a central role is played by the ramification locus of the projection. Additionally, we provide tools for counting the number of critical points over projective varieties, and discuss specific cases arising from deep learning. Our work bridges tools from algebraic geometry with ideas from machine learning, and it extends the line of literature around the Euclidean distance degree to the degenerate setting.

Sprecher Networks: A Parameter-Efficient Kolmogorov-Arnold Architecture

We present Sprecher Networks (SNs), a family of trainable neural architectures inspired by the classical Kolmogorov-Arnold-Sprecher (KAS) construction for approximating multivariate continuous functions. Distinct from Multi-Layer Perceptrons (MLPs) with fixed node activations and Kolmogorov-Arnold Networks (KANs) featuring learnable edge activations, SNs utilize shared, learnable splines (monotonic and general) within structured blocks incorporating explicit shift parameters and mixing weights. Our approach directly realizes Sprecher's specific 1965 sum of shifted splines formula in its single-layer variant and extends it to deeper, multi-layer compositions. We further enhance the architecture with optional lateral mixing connections that enable intra-block communication between output dimensions, providing a parameter-efficient alternative to full attention mechanisms. Beyond parameter efficiency with $O(LN + LG)$ scaling (where $G$ is the knot count of the shared splines) versus MLPs' $O(LN^2)$, SNs admit a sequential evaluation strategy that reduces peak forward-intermediate memory from $O(N^2)$ to $O(N)$ (treating batch size as constant), making much wider architectures feasible under memory constraints. We demonstrate empirically that composing these blocks into deep networks leads to highly parameter and memory-efficient models, discuss theoretical motivations, and compare SNs with related architectures (MLPs, KANs, and networks with learnable node activations).

The Riemannian Geometry associated to Gradient Flows of Linear Convolutional Networks

We study geometric properties of the gradient flow for learning deep linear convolutional networks. For linear fully connected networks, it has been shown recently that the corresponding gradient flow on parameter space can be written as a Riemannian gradient flow on function space (i.e., on the product of weight matrices) if the initialization satisfies a so-called balancedness condition. We establish that the gradient flow on parameter space for learning linear convolutional networks can be written as a Riemannian gradient flow on function space regardless of the initialization. This result holds for $D$-dimensional convolutions with $D \geq 2$, and for $D =1$ it holds if all so-called strides of the convolutions are greater than one. The corresponding Riemannian metric depends on the initialization.

Learning on a Razor's Edge: the Singularity Bias of Polynomial Neural Networks

Deep neural networks often infer sparse representations, converging to a subnetwork during the learning process. In this work, we theoretically analyze subnetworks and their bias through the lens of algebraic geometry. We consider fully-connected networks with polynomial activation functions, and focus on the geometry of the function space they parametrize, often referred to as neuromanifold. First, we compute the dimension of the subspace of the neuromanifold parametrized by subnetworks. Second, we show that this subspace is singular. Third, we argue that such singularities often correspond to critical points of the training dynamics. Lastly, we discuss convolutional networks, for which subnetworks and singularities are similarly related, but the bias does not arise.

An Algebraic Geometry Approach to Viewing Graph Solvability

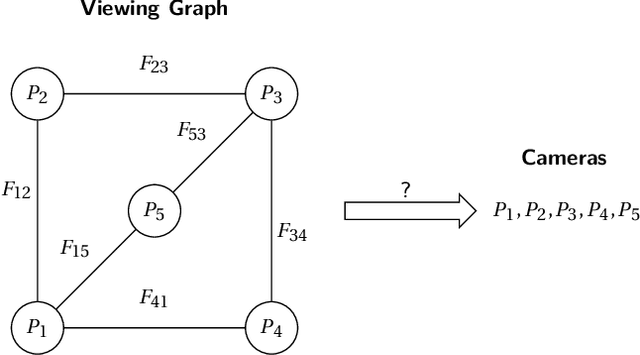
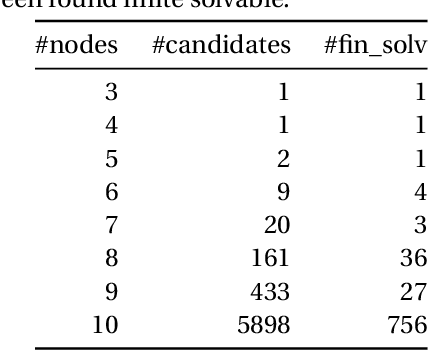
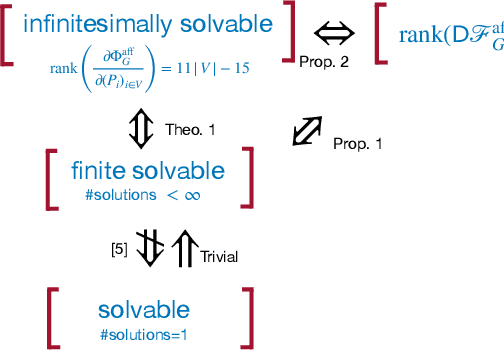
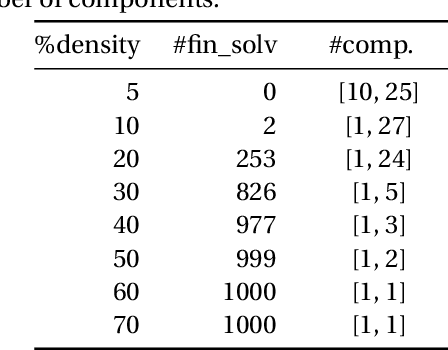
The concept of viewing graph solvability has gained significant interest in the context of structure-from-motion. A viewing graph is a mathematical structure where nodes are associated to cameras and edges represent the epipolar geometry connecting overlapping views. Solvability studies under which conditions the cameras are uniquely determined by the graph. In this paper we propose a novel framework for analyzing solvability problems based on Algebraic Geometry, demonstrating its potential in understanding structure-from-motion graphs and proving a conjecture that was previously proposed.

A Framework for Reducing the Complexity of Geometric Vision Problems and its Application to Two-View Triangulation with Approximation Bounds

In this paper, we present a new framework for reducing the computational complexity of geometric vision problems through targeted reweighting of the cost functions used to minimize reprojection errors. Triangulation - the task of estimating a 3D point from noisy 2D projections across multiple images - is a fundamental problem in multiview geometry and Structure-from-Motion (SfM) pipelines. We apply our framework to the two-view case and demonstrate that optimal triangulation, which requires solving a univariate polynomial of degree six, can be simplified through cost function reweighting reducing the polynomial degree to two. This reweighting yields a closed-form solution while preserving strong geometric accuracy. We derive optimal weighting strategies, establish theoretical bounds on the approximation error, and provide experimental results on real data demonstrating the effectiveness of the proposed approach compared to standard methods. Although this work focuses on two-view triangulation, the framework generalizes to other geometric vision problems.

PLMP -- Point-Line Minimal Problems for Projective SfM

We completely classify all minimal problems for Structure-from-Motion (SfM) where arrangements of points and lines are fully observed by multiple uncalibrated pinhole cameras. We find 291 minimal problems, 73 of which have unique solutions and can thus be solved linearly. Two of the linear problems allow an arbitrary number of views, while all other minimal problems have at most 9 cameras. All minimal problems have at most 7 points and at most 12 lines. We compute the number of solutions of each minimal problem, as this gives a measurement of the problem's intrinsic difficulty, and find that these number are relatively low (e.g., when comparing with minimal problems for calibrated cameras). Finally, by exploring stabilizer subgroups of subarrangements, we develop a geometric and systematic way to 1) factorize minimal problems into smaller problems, 2) identify minimal problems in underconstrained problems, and 3) formally prove non-minimality.

An Invitation to Neuroalgebraic Geometry

In this expository work, we promote the study of function spaces parameterized by machine learning models through the lens of algebraic geometry. To this end, we focus on algebraic models, such as neural networks with polynomial activations, whose associated function spaces are semi-algebraic varieties. We outline a dictionary between algebro-geometric invariants of these varieties, such as dimension, degree, and singularities, and fundamental aspects of machine learning, such as sample complexity, expressivity, training dynamics, and implicit bias. Along the way, we review the literature and discuss ideas beyond the algebraic domain. This work lays the foundations of a research direction bridging algebraic geometry and deep learning, that we refer to as neuroalgebraic geometry.

On the Geometry and Optimization of Polynomial Convolutional Networks

We study convolutional neural networks with monomial activation functions. Specifically, we prove that their parameterization map is regular and is an isomorphism almost everywhere, up to rescaling the filters. By leveraging on tools from algebraic geometry, we explore the geometric properties of the image in function space of this map -- typically referred to as neuromanifold. In particular, we compute the dimension and the degree of the neuromanifold, which measure the expressivity of the model, and describe its singularities. Moreover, for a generic large dataset, we derive an explicit formula that quantifies the number of critical points arising in the optimization of a regression loss.

Geometry of Lightning Self-Attention: Identifiability and Dimension

We consider function spaces defined by self-attention networks without normalization, and theoretically analyze their geometry. Since these networks are polynomial, we rely on tools from algebraic geometry. In particular, we study the identifiability of deep attention by providing a description of the generic fibers of the parametrization for an arbitrary number of layers and, as a consequence, compute the dimension of the function space. Additionally, for a single-layer model, we characterize the singular and boundary points. Finally, we formulate a conjectural extension of our results to normalized self-attention networks, prove it for a single layer, and numerically verify it in the deep case.