Geometry and Optimization of Shallow Polynomial Networks

We study shallow neural networks with polynomial activations. The function space for these models can be identified with a set of symmetric tensors with bounded rank. We describe general features of these networks, focusing on the relationship between width and optimization. We then consider teacher-student problems, that can be viewed as a problem of low-rank tensor approximation with respect to a non-standard inner product that is induced by the data distribution. In this setting, we introduce a teacher-metric discriminant which encodes the qualitative behavior of the optimization as a function of the training data distribution. Finally, we focus on networks with quadratic activations, presenting an in-depth analysis of the optimization landscape. In particular, we present a variation of the Eckart-Young Theorem characterizing all critical points and their Hessian signatures for teacher-student problems with quadratic networks and Gaussian training data.

Symmetry & Critical Points

Critical points of an invariant function may or may not be symmetric. We prove, however, that if a symmetric critical point exists, those adjacent to it are generically symmetry breaking. This mathematical mechanism is shown to carry important implications for our ability to efficiently minimize invariant nonconvex functions, in particular those associated with neural networks.

Hidden Minima in Two-Layer ReLU Networks

The optimization problem associated to fitting two-layer ReLU networks having $d$~inputs, $k$~neurons, and labels generated by a target network, is considered. Two categories of infinite families of minima, giving one minimum per $d$ and $k$, were recently found. The loss at minima belonging to the first category converges to zero as $d$ increases. In the second category, the loss remains bounded away from zero. That being so, how may one avoid minima belonging to the latter category? Fortunately, such minima are never detected by standard optimization methods. Motivated by questions concerning the nature of this phenomenon, we develop methods to study distinctive analytic properties of hidden minima. By existing analyses, the Hessian spectrum of both categories agree modulus $O(d^{-1/2})$-terms -- not promising. Thus, rather, our investigation proceeds by studying curves along which the loss is minimized or maximized, referred to as tangency arcs. We prove that pure, seemingly remote, group representation-theoretic considerations concerning the arrangement of subspaces invariant to the action of subgroups of $S_d$, the symmetry group over $d$ symbols, relative to ones fixed by the action yield a precise description of all finitely many admissible types of tangency arcs. The general results applied for the loss function reveal that arcs emanating from hidden minima differ, characteristically, by their structure and symmetry, precisely on account of the $O(d^{-1/2})$-eigenvalue terms absent in previous work, indicating the subtly of the analysis. The theoretical results, stated and proved for o-minimal structures, show that the set comprising all tangency arcs is topologically sufficiently tame, permitting a numerical construction of tangency arcs, and ultimately, a comparison of how minima from both categories are positioned relative to adjacent critical points.

Symmetry & Critical Points for Symmetric Tensor Decomposition Problems

We consider the non-convex optimization problem associated with the decomposition of a real symmetric tensor into a sum of rank one terms. Use is made of the rich symmetry structure to derive Puiseux series representations of families of critical points, and so obtain precise analytic estimates on the critical values and the Hessian spectrum. The sharp results make possible an analytic characterization of various geometric obstructions to local optimization methods, revealing in particular a complex array of saddles and local minima which differ by their symmetry, structure and analytic properties. A desirable phenomenon, occurring for all critical points considered, concerns the index of a point, i.e., the number of negative Hessian eigenvalues, increasing with the value of the objective function. Lastly, a Newton polytope argument is used to give a complete enumeration of all critical points of fixed symmetry, and it is shown that contrarily to the set of global minima which remains invariant under different choices of tensor norms, certain families of non-global minima emerge, others disappear.

Annihilation of Spurious Minima in Two-Layer ReLU Networks

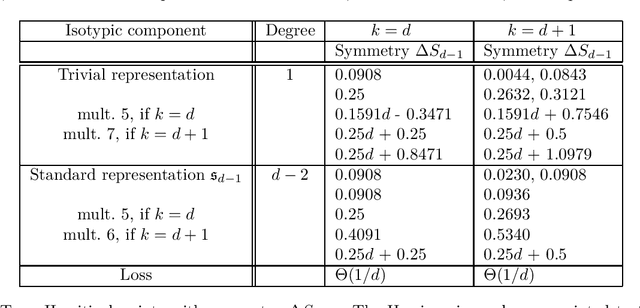
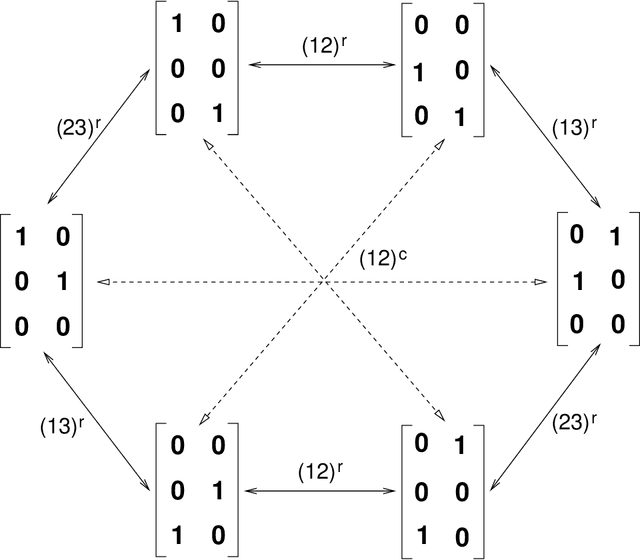
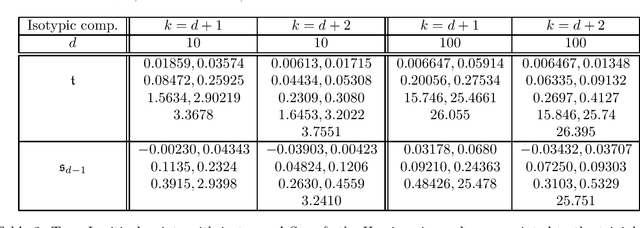
We study the optimization problem associated with fitting two-layer ReLU neural networks with respect to the squared loss, where labels are generated by a target network. Use is made of the rich symmetry structure to develop a novel set of tools for studying the mechanism by which over-parameterization annihilates spurious minima. Sharp analytic estimates are obtained for the loss and the Hessian spectrum at different minima, and it is proved that adding neurons can turn symmetric spurious minima into saddles; minima of lesser symmetry require more neurons. Using Cauchy's interlacing theorem, we prove the existence of descent directions in certain subspaces arising from the symmetry structure of the loss function. This analytic approach uses techniques, new to the field, from algebraic geometry, representation theory and symmetry breaking, and confirms rigorously the effectiveness of over-parameterization in making the associated loss landscape accessible to gradient-based methods. For a fixed number of neurons and inputs, the spectral results remain true under symmetry breaking perturbation of the target.

Analytic Study of Families of Spurious Minima in Two-Layer ReLU Neural Networks

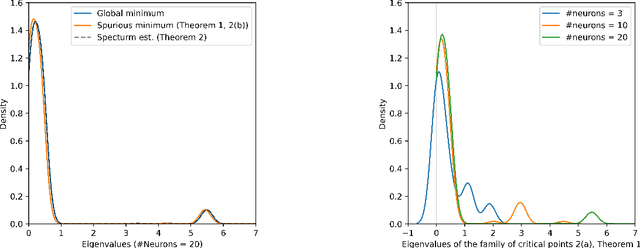
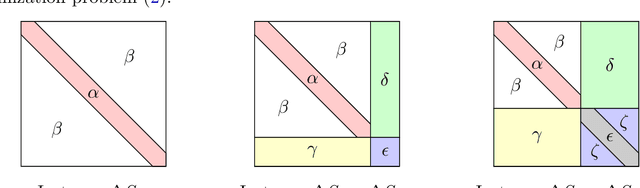
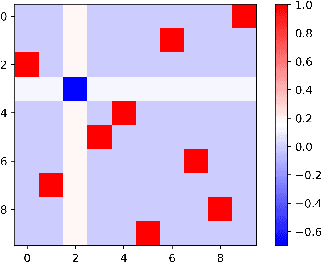
We study the optimization problem associated with fitting two-layer ReLU neural networks with respect to the squared loss, where labels are generated by a target network. We make use of the rich symmetry structure to develop a novel set of tools for studying families of spurious minima. In contrast to existing approaches which operate in limiting regimes, our technique directly addresses the nonconvex loss landscape for a finite number of inputs $d$ and neurons $k$, and provides analytic, rather than heuristic, information. In particular, we derive analytic estimates for the loss at different minima, and prove that modulo $O(d^{-1/2})$-terms the Hessian spectrum concentrates near small positive constants, with the exception of $\Theta(d)$ eigenvalues which grow linearly with~$d$. We further show that the Hessian spectrum at global and spurious minima coincide to $O(d^{-1/2})$-order, thus challenging our ability to argue about statistical generalization through local curvature. Lastly, our technique provides the exact \emph{fractional} dimensionality at which families of critical points turn from saddles into spurious minima. This makes possible the study of the creation and the annihilation of spurious minima using powerful tools from equivariant bifurcation theory.

Equivariant bifurcation, quadratic equivariants, and symmetry breaking for the standard representation of $S_n$

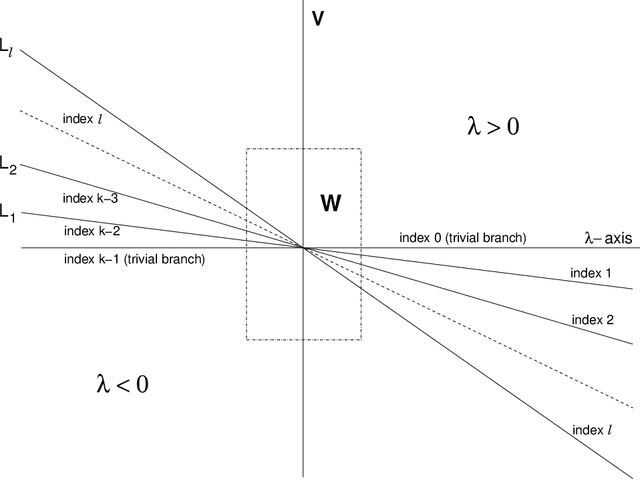
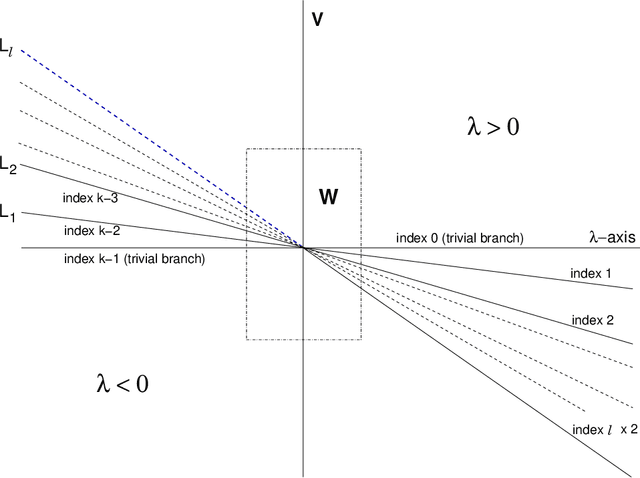
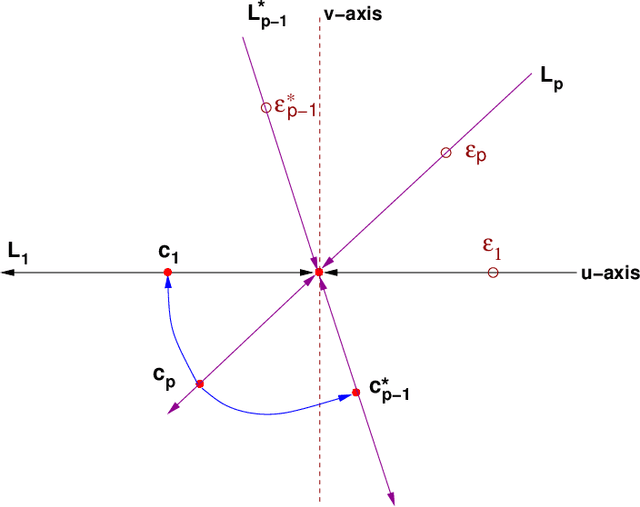
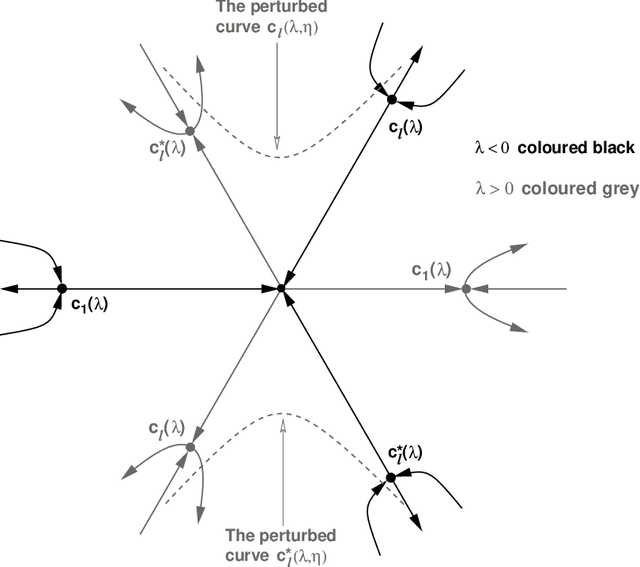
Motivated by questions originating from the study of a class of shallow student-teacher neural networks, methods are developed for the analysis of spurious minima in classes of gradient equivariant dynamics related to neural nets. In the symmetric case, methods depend on the generic equivariant bifurcation theory of irreducible representations of the symmetric group on $n$ symbols, $S_n$; in particular, the standard representation of $S_n$. It is shown that spurious minima do not arise from spontaneous symmetry breaking but rather through a complex deformation of the landscape geometry that can be encoded by a generic $S_n$-equivariant bifurcation. We describe minimal models for forced symmetry breaking that give a lower bound on the dynamic complexity involved in the creation of spurious minima when there is no symmetry. Results on generic bifurcation when there are quadratic equivariants are also proved; this work extends and clarifies results of Ihrig & Golubitsky and Chossat, Lauterback & Melbourne on the instability of solutions when there are quadratic equivariants.

Symmetry Breaking in Symmetric Tensor Decomposition

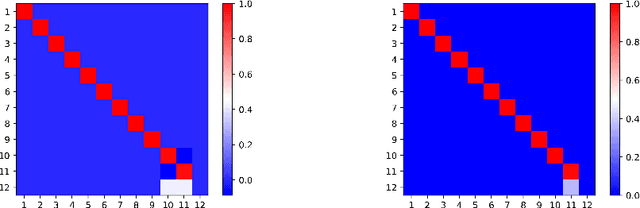
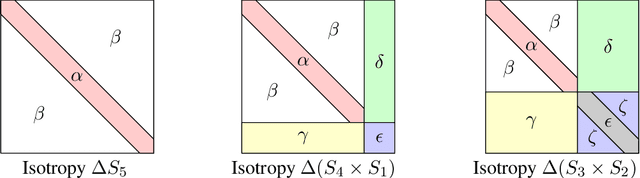
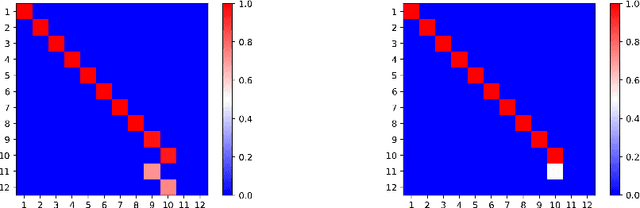
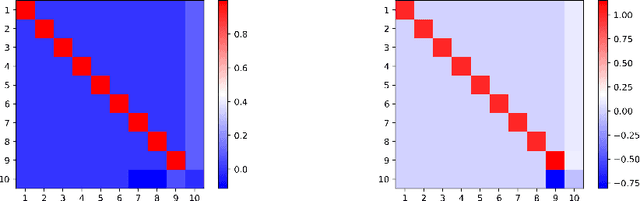
In this note, we consider the optimization problem associated with computing the rank decomposition of a symmetric tensor. We show that, in a well-defined sense, minima in this highly nonconvex optimization problem break the symmetry of the target tensor -- but not too much. This phenomenon of symmetry breaking applies to various choices of tensor norms, and makes it possible to study the optimization landscape using a set of recently-developed symmetry-based analytical tools. The fact that the objective function under consideration is a multivariate polynomial allows us to apply symbolic methods from computational algebra to obtain more refined information on the symmetry breaking phenomenon.

Analytic Characterization of the Hessian in Shallow ReLU Models: A Tale of Symmetry

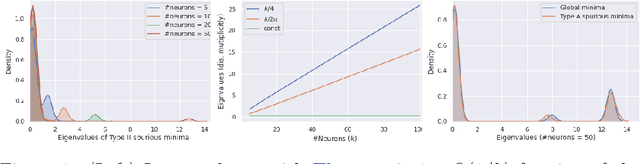
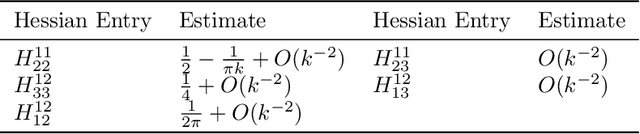
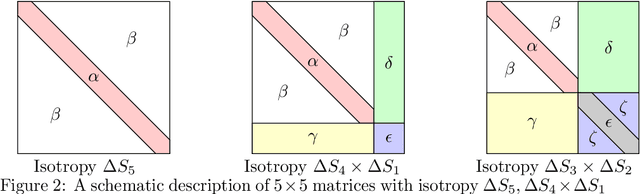
We consider the optimization problem associated with fitting two-layers ReLU networks with $k$ neurons. We leverage the rich symmetry structure to analytically characterize the Hessian and its spectral density at various families of spurious local minima. In particular, we prove that for standard $d$-dimensional Gaussian inputs with $d\ge k$: (a) of the $dk$ eigenvalues corresponding to the weights of the first layer, $dk - O(d)$ concentrate near zero, (b) $\Omega(d)$ of the remaining eigenvalues grow linearly with $k$. Although this phenomenon of extremely skewed spectrum has been observed many times before, to the best of our knowledge, this is the first time it has been established rigorously. Our analytic approach uses techniques, new to the field, from symmetry breaking and representation theory, and carries important implications for our ability to argue about statistical generalization through local curvature.

Second-Order Information in Non-Convex Stochastic Optimization: Power and Limitations

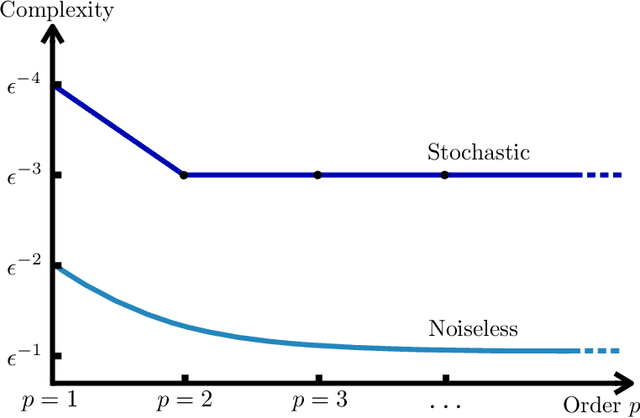
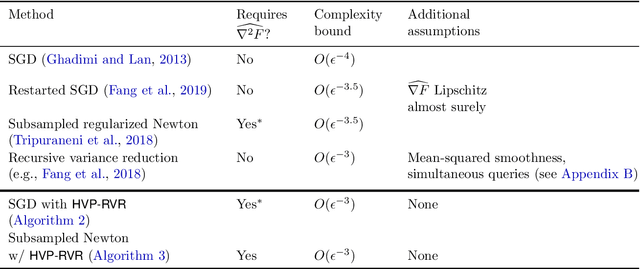
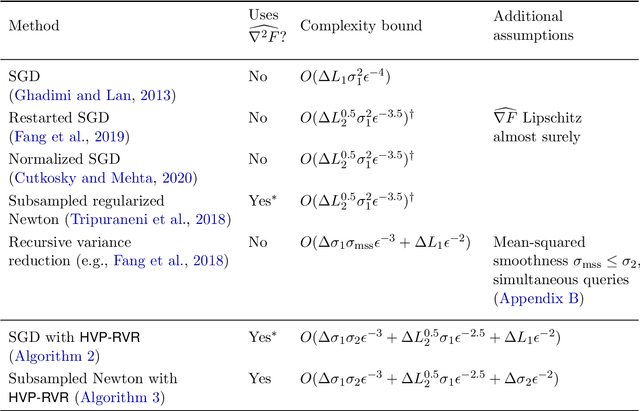
We design an algorithm which finds an $\epsilon$-approximate stationary point (with $\|\nabla F(x)\|\le \epsilon$) using $O(\epsilon^{-3})$ stochastic gradient and Hessian-vector products, matching guarantees that were previously available only under a stronger assumption of access to multiple queries with the same random seed. We prove a lower bound which establishes that this rate is optimal and---surprisingly---that it cannot be improved using stochastic $p$th order methods for any $p\ge 2$, even when the first $p$ derivatives of the objective are Lipschitz. Together, these results characterize the complexity of non-convex stochastic optimization with second-order methods and beyond. Expanding our scope to the oracle complexity of finding $(\epsilon,\gamma)$-approximate second-order stationary points, we establish nearly matching upper and lower bounds for stochastic second-order methods. Our lower bounds here are novel even in the noiseless case.