How Many Tokens Do 3D Point Cloud Transformer Architectures Really Need?

Recent advances in 3D point cloud transformers have led to state-of-the-art results in tasks such as semantic segmentation and reconstruction. However, these models typically rely on dense token representations, incurring high computational and memory costs during training and inference. In this work, we present the finding that tokens are remarkably redundant, leading to substantial inefficiency. We introduce gitmerge3D, a globally informed graph token merging method that can reduce the token count by up to 90-95% while maintaining competitive performance. This finding challenges the prevailing assumption that more tokens inherently yield better performance and highlights that many current models are over-tokenized and under-optimized for scalability. We validate our method across multiple 3D vision tasks and show consistent improvements in computational efficiency. This work is the first to assess redundancy in large-scale 3D transformer models, providing insights into the development of more efficient 3D foundation architectures. Our code and checkpoints are publicly available at https://gitmerge3d.github.io

S-Chain: Structured Visual Chain-of-Thought For Medicine

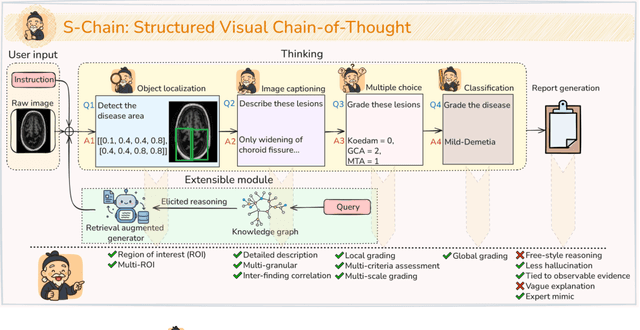
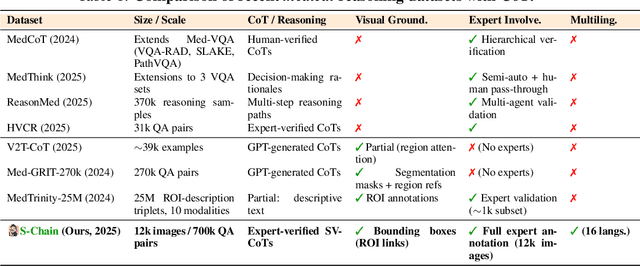
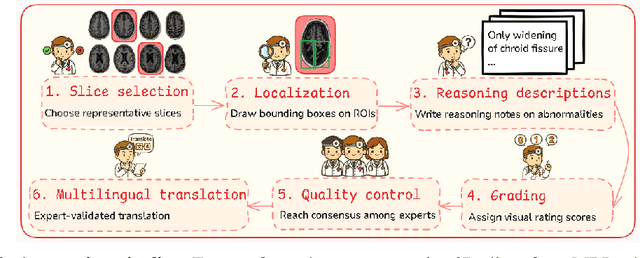
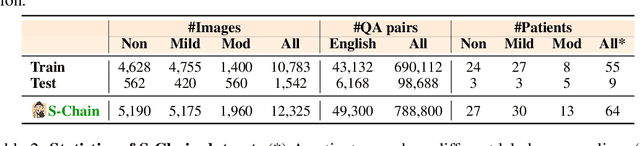
Faithful reasoning in medical vision-language models (VLMs) requires not only accurate predictions but also transparent alignment between textual rationales and visual evidence. While Chain-of-Thought (CoT) prompting has shown promise in medical visual question answering (VQA), no large-scale expert-level dataset has captured stepwise reasoning with precise visual grounding. We introduce S-Chain, the first large-scale dataset of 12,000 expert-annotated medical images with bounding boxes and structured visual CoT (SV-CoT), explicitly linking visual regions to reasoning steps. The dataset further supports 16 languages, totaling over 700k VQA pairs for broad multilingual applicability. Using S-Chain, we benchmark state-of-the-art medical VLMs (ExGra-Med, LLaVA-Med) and general-purpose VLMs (Qwen2.5-VL, InternVL2.5), showing that SV-CoT supervision significantly improves interpretability, grounding fidelity, and robustness. Beyond benchmarking, we study its synergy with retrieval-augmented generation, revealing how domain knowledge and visual grounding interact during autoregressive reasoning. Finally, we propose a new mechanism that strengthens the alignment between visual evidence and reasoning, improving both reliability and efficiency. S-Chain establishes a new benchmark for grounded medical reasoning and paves the way toward more trustworthy and explainable medical VLMs.

Learning the Neighborhood: Contrast-Free Multimodal Self-Supervised Molecular Graph Pretraining

High-quality molecular representations are essential for property prediction and molecular design, yet large labeled datasets remain scarce. While self-supervised pretraining on molecular graphs has shown promise, many existing approaches either depend on hand-crafted augmentations or complex generative objectives, and often rely solely on 2D topology, leaving valuable 3D structural information underutilized. To address this gap, we introduce C-FREE (Contrast-Free Representation learning on Ego-nets), a simple framework that integrates 2D graphs with ensembles of 3D conformers. C-FREE learns molecular representations by predicting subgraph embeddings from their complementary neighborhoods in the latent space, using fixed-radius ego-nets as modeling units across different conformers. This design allows us to integrate both geometric and topological information within a hybrid Graph Neural Network (GNN)-Transformer backbone, without negatives, positional encodings, or expensive pre-processing. Pretraining on the GEOM dataset, which provides rich 3D conformational diversity, C-FREE achieves state-of-the-art results on MoleculeNet, surpassing contrastive, generative, and other multimodal self-supervised methods. Fine-tuning across datasets with diverse sizes and molecule types further demonstrates that pretraining transfers effectively to new chemical domains, highlighting the importance of 3D-informed molecular representations.

Learning (Approximately) Equivariant Networks via Constrained Optimization

Equivariant neural networks are designed to respect symmetries through their architecture, boosting generalization and sample efficiency when those symmetries are present in the data distribution. Real-world data, however, often departs from perfect symmetry because of noise, structural variation, measurement bias, or other symmetry-breaking effects. Strictly equivariant models may struggle to fit the data, while unconstrained models lack a principled way to leverage partial symmetries. Even when the data is fully symmetric, enforcing equivariance can hurt training by limiting the model to a restricted region of the parameter space. Guided by homotopy principles, where an optimization problem is solved by gradually transforming a simpler problem into a complex one, we introduce Adaptive Constrained Equivariance (ACE), a constrained optimization approach that starts with a flexible, non-equivariant model and gradually reduces its deviation from equivariance. This gradual tightening smooths training early on and settles the model at a data-driven equilibrium, balancing between equivariance and non-equivariance. Across multiple architectures and tasks, our method consistently improves performance metrics, sample efficiency, and robustness to input perturbations compared with strictly equivariant models and heuristic equivariance relaxations.

CALM-PDE: Continuous and Adaptive Convolutions for Latent Space Modeling of Time-dependent PDEs

Solving time-dependent Partial Differential Equations (PDEs) using a densely discretized spatial domain is a fundamental problem in various scientific and engineering disciplines, including modeling climate phenomena and fluid dynamics. However, performing these computations directly in the physical space often incurs significant computational costs. To address this issue, several neural surrogate models have been developed that operate in a compressed latent space to solve the PDE. While these approaches reduce computational complexity, they often use Transformer-based attention mechanisms to handle irregularly sampled domains, resulting in increased memory consumption. In contrast, convolutional neural networks allow memory-efficient encoding and decoding but are limited to regular discretizations. Motivated by these considerations, we propose CALM-PDE, a model class that efficiently solves arbitrarily discretized PDEs in a compressed latent space. We introduce a novel continuous convolution-based encoder-decoder architecture that uses an epsilon-neighborhood-constrained kernel and learns to apply the convolution operator to adaptive and optimized query points. We demonstrate the effectiveness of CALM-PDE on a diverse set of PDEs with both regularly and irregularly sampled spatial domains. CALM-PDE is competitive with or outperforms existing baseline methods while offering significant improvements in memory and inference time efficiency compared to Transformer-based methods.

LOGLO-FNO: Efficient Learning of Local and Global Features in Fourier Neural Operators

Modeling high-frequency information is a critical challenge in scientific machine learning. For instance, fully turbulent flow simulations of Navier-Stokes equations at Reynolds numbers 3500 and above can generate high-frequency signals due to swirling fluid motions caused by eddies and vortices. Faithfully modeling such signals using neural networks depends on accurately reconstructing moderate to high frequencies. However, it has been well known that deep neural nets exhibit the so-called spectral bias toward learning low-frequency components. Meanwhile, Fourier Neural Operators (FNOs) have emerged as a popular class of data-driven models in recent years for solving Partial Differential Equations (PDEs) and for surrogate modeling in general. Although impressive results have been achieved on several PDE benchmark problems, FNOs often perform poorly in learning non-dominant frequencies characterized by local features. This limitation stems from the spectral bias inherent in neural networks and the explicit exclusion of high-frequency modes in FNOs and their variants. Therefore, to mitigate these issues and improve FNO's spectral learning capabilities to represent a broad range of frequency components, we propose two key architectural enhancements: (i) a parallel branch performing local spectral convolutions (ii) a high-frequency propagation module. Moreover, we propose a novel frequency-sensitive loss term based on radially binned spectral errors. This introduction of a parallel branch for local convolutions reduces number of trainable parameters by up to 50% while achieving the accuracy of baseline FNO that relies solely on global convolutions. Experiments on three challenging PDE problems in fluid mechanics and biological pattern formation, and the qualitative and spectral analysis of predictions show the effectiveness of our method over the state-of-the-art neural operator baselines.

Preference-Based Gradient Estimation for ML-Based Approximate Combinatorial Optimization

Combinatorial optimization (CO) problems arise in a wide range of fields from medicine to logistics and manufacturing. While exact solutions are often not necessary, many applications require finding high-quality solutions quickly. For this purpose, we propose a data-driven approach to improve existing non-learned approximation algorithms for CO. We parameterize the approximation algorithm and train a graph neural network (GNN) to predict parameter values that lead to the best possible solutions. Our pipeline is trained end-to-end in a self-supervised fashion using gradient estimation, treating the approximation algorithm as a black box. We propose a novel gradient estimation scheme for this purpose, which we call preference-based gradient estimation. Our approach combines the benefits of the neural network and the non-learned approximation algorithm: The GNN leverages the information from the dataset to allow the approximation algorithm to find better solutions, while the approximation algorithm guarantees that the solution is feasible. We validate our approach on two well-known combinatorial optimization problems, the travelling salesman problem and the minimum k-cut problem, and show that our method is competitive with state of the art learned CO solvers.

Position: Graph Learning Will Lose Relevance Due To Poor Benchmarks

While machine learning on graphs has demonstrated promise in drug design and molecular property prediction, significant benchmarking challenges hinder its further progress and relevance. Current benchmarking practices often lack focus on transformative, real-world applications, favoring narrow domains like two-dimensional molecular graphs over broader, impactful areas such as combinatorial optimization, relational databases, or chip design. Additionally, many benchmark datasets poorly represent the underlying data, leading to inadequate abstractions and misaligned use cases. Fragmented evaluations and an excessive focus on accuracy further exacerbate these issues, incentivizing overfitting rather than fostering generalizable insights. These limitations have prevented the development of truly useful graph foundation models. This position paper calls for a paradigm shift toward more meaningful benchmarks, rigorous evaluation protocols, and stronger collaboration with domain experts to drive impactful and reliable advances in graph learning research, unlocking the potential of graph learning.

Tractable Transformers for Flexible Conditional Generation

Non-autoregressive (NAR) generative models are valuable because they can handle diverse conditional generation tasks in a more principled way than their autoregressive (AR) counterparts, which are constrained by sequential dependency requirements. Recent advancements in NAR models, such as diffusion language models, have demonstrated superior performance in unconditional generation compared to AR models (e.g., GPTs) of similar sizes. However, such improvements do not always lead to improved conditional generation performance. We show that a key reason for this gap is the difficulty in generalizing to conditional probability queries unseen during training. As a result, strong unconditional generation performance does not guarantee high-quality conditional generation. This paper proposes Tractable Transformers (Tracformer), a Transformer-based generative model that is more robust to different conditional generation tasks. Unlike existing models that rely solely on global contextual features derived from full inputs, Tracformers incorporate a sparse Transformer encoder to capture both local and global contextual information. This information is routed through a decoder for conditional generation. Empirical results demonstrate that Tracformers achieve state-of-the-art conditional generation performance on text modeling compared to recent diffusion and AR model baselines.

On Zero-Initialized Attention: Optimal Prompt and Gating Factor Estimation

The LLaMA-Adapter has recently emerged as an efficient fine-tuning technique for LLaMA models, leveraging zero-initialized attention to stabilize training and enhance performance. However, despite its empirical success, the theoretical foundations of zero-initialized attention remain largely unexplored. In this paper, we provide a rigorous theoretical analysis, establishing a connection between zero-initialized attention and mixture-of-expert models. We prove that both linear and non-linear prompts, along with gating functions, can be optimally estimated, with non-linear prompts offering greater flexibility for future applications. Empirically, we validate our findings on the open LLM benchmarks, demonstrating that non-linear prompts outperform linear ones. Notably, even with limited training data, both prompt types consistently surpass vanilla attention, highlighting the robustness and adaptability of zero-initialized attention.