Flow-Based Policy for Online Reinforcement Learning

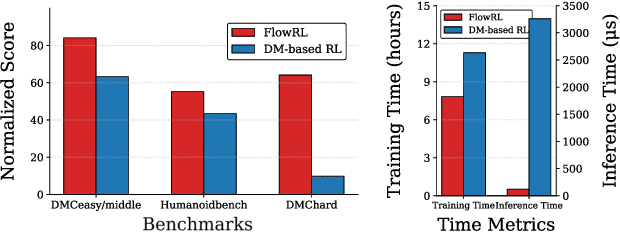
We present \textbf{FlowRL}, a novel framework for online reinforcement learning that integrates flow-based policy representation with Wasserstein-2-regularized optimization. We argue that in addition to training signals, enhancing the expressiveness of the policy class is crucial for the performance gains in RL. Flow-based generative models offer such potential, excelling at capturing complex, multimodal action distributions. However, their direct application in online RL is challenging due to a fundamental objective mismatch: standard flow training optimizes for static data imitation, while RL requires value-based policy optimization through a dynamic buffer, leading to difficult optimization landscapes. FlowRL first models policies via a state-dependent velocity field, generating actions through deterministic ODE integration from noise. We derive a constrained policy search objective that jointly maximizes Q through the flow policy while bounding the Wasserstein-2 distance to a behavior-optimal policy implicitly derived from the replay buffer. This formulation effectively aligns the flow optimization with the RL objective, enabling efficient and value-aware policy learning despite the complexity of the policy class. Empirical evaluations on DMControl and Humanoidbench demonstrate that FlowRL achieves competitive performance in online reinforcement learning benchmarks.

Multi-segment Soft Robot Control via Deep Koopman-based Model Predictive Control

Soft robots, compared to regular rigid robots, as their multiple segments with soft materials bring flexibility and compliance, have the advantages of safe interaction and dexterous operation in the environment. However, due to its characteristics of high dimensional, nonlinearity, time-varying nature, and infinite degree of freedom, it has been challenges in achieving precise and dynamic control such as trajectory tracking and position reaching. To address these challenges, we propose a framework of Deep Koopman-based Model Predictive Control (DK-MPC) for handling multi-segment soft robots. We first employ a deep learning approach with sampling data to approximate the Koopman operator, which therefore linearizes the high-dimensional nonlinear dynamics of the soft robots into a finite-dimensional linear representation. Secondly, this linearized model is utilized within a model predictive control framework to compute optimal control inputs that minimize the tracking error between the desired and actual state trajectories. The real-world experiments on the soft robot "Chordata" demonstrate that DK-MPC could achieve high-precision control, showing the potential of DK-MPC for future applications to soft robots.

Model-based Constrained MDP for Budget Allocation in Sequential Incentive Marketing

Sequential incentive marketing is an important approach for online businesses to acquire customers, increase loyalty and boost sales. How to effectively allocate the incentives so as to maximize the return (e.g., business objectives) under the budget constraint, however, is less studied in the literature. This problem is technically challenging due to the facts that 1) the allocation strategy has to be learned using historically logged data, which is counterfactual in nature, and 2) both the optimality and feasibility (i.e., that cost cannot exceed budget) needs to be assessed before being deployed to online systems. In this paper, we formulate the problem as a constrained Markov decision process (CMDP). To solve the CMDP problem with logged counterfactual data, we propose an efficient learning algorithm which combines bisection search and model-based planning. First, the CMDP is converted into its dual using Lagrangian relaxation, which is proved to be monotonic with respect to the dual variable. Furthermore, we show that the dual problem can be solved by policy learning, with the optimal dual variable being found efficiently via bisection search (i.e., by taking advantage of the monotonicity). Lastly, we show that model-based planing can be used to effectively accelerate the joint optimization process without retraining the policy for every dual variable. Empirical results on synthetic and real marketing datasets confirm the effectiveness of our methods.

Prior-Enhanced Few-Shot Segmentation with Meta-Prototypes

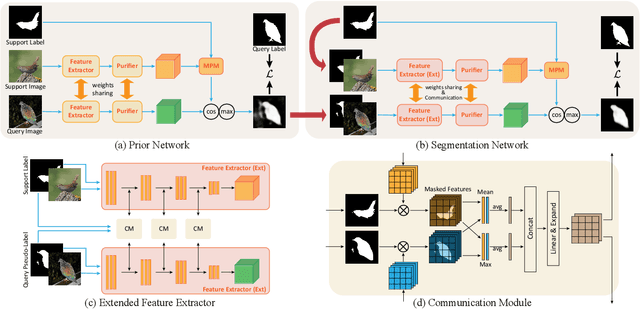
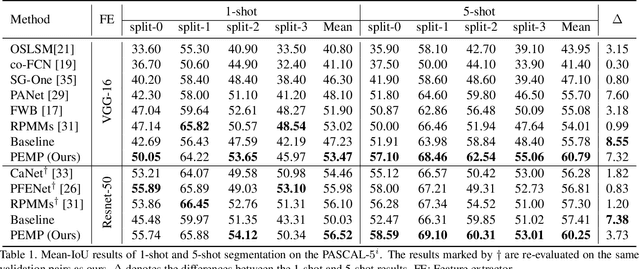
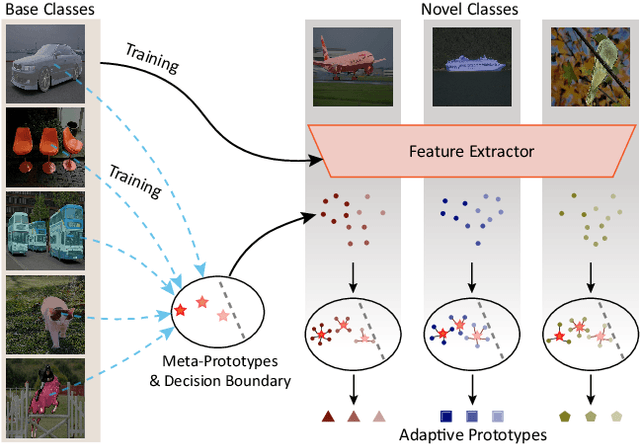
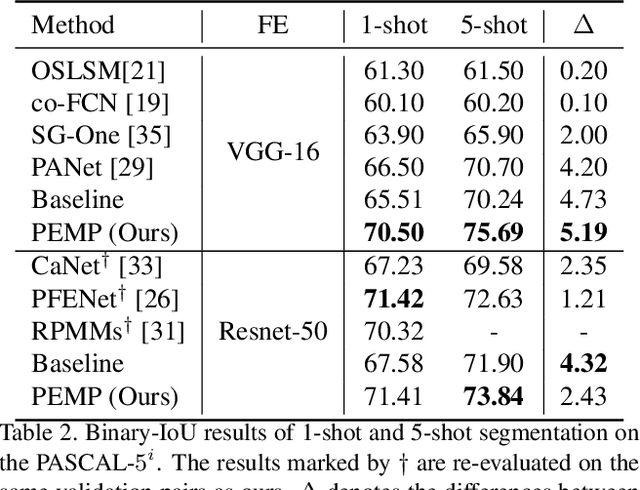
Few-shot segmentation~(FSS) performance has been extensively promoted by introducing episodic training and class-wise prototypes. However, the FSS problem remains challenging due to three limitations: (1) Models are distracted by task-unrelated information; (2) The representation ability of a single prototype is limited; (3) Class-related prototypes ignore the prior knowledge of base classes. We propose the Prior-Enhanced network with Meta-Prototypes to tackle these limitations. The prior-enhanced network leverages the support and query (pseudo-) labels in feature extraction, which guides the model to focus on the task-related features of the foreground objects, and suppress much noise due to the lack of supervised knowledge. Moreover, we introduce multiple meta-prototypes to encode hierarchical features and learn class-agnostic structural information. The hierarchical features help the model highlight the decision boundary and focus on hard pixels, and the structural information learned from base classes is treated as the prior knowledge for novel classes. Experiments show that our method achieves the mean-IoU scores of 60.79% and 41.16% on PASCAL-$5^i$ and COCO-$20^i$, outperforming the state-of-the-art method by 3.49% and 5.64% in the 5-shot setting. Moreover, comparing with 1-shot results, our method promotes 5-shot accuracy by 3.73% and 10.32% on the above two benchmarks. The source code of our method is available at https://github.com/Jarvis73/PEMP.