Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

RelBench: A Benchmark for Deep Learning on Relational Databases

We present RelBench, a public benchmark for solving predictive tasks over relational databases with graph neural networks. RelBench provides databases and tasks spanning diverse domains and scales, and is intended to be a foundational infrastructure for future research. We use RelBench to conduct the first comprehensive study of Relational Deep Learning (RDL) (Fey et al., 2024), which combines graph neural network predictive models with (deep) tabular models that extract initial entity-level representations from raw tables. End-to-end learned RDL models fully exploit the predictive signal encoded in primary-foreign key links, marking a significant shift away from the dominant paradigm of manual feature engineering combined with tabular models. To thoroughly evaluate RDL against this prior gold-standard, we conduct an in-depth user study where an experienced data scientist manually engineers features for each task. In this study, RDL learns better models whilst reducing human work needed by more than an order of magnitude. This demonstrates the power of deep learning for solving predictive tasks over relational databases, opening up many new research opportunities enabled by RelBench.

Relational Deep Learning: Graph Representation Learning on Relational Databases

Much of the world's most valued data is stored in relational databases and data warehouses, where the data is organized into many tables connected by primary-foreign key relations. However, building machine learning models using this data is both challenging and time consuming. The core problem is that no machine learning method is capable of learning on multiple tables interconnected by primary-foreign key relations. Current methods can only learn from a single table, so the data must first be manually joined and aggregated into a single training table, the process known as feature engineering. Feature engineering is slow, error prone and leads to suboptimal models. Here we introduce an end-to-end deep representation learning approach to directly learn on data laid out across multiple tables. We name our approach Relational Deep Learning (RDL). The core idea is to view relational databases as a temporal, heterogeneous graph, with a node for each row in each table, and edges specified by primary-foreign key links. Message Passing Graph Neural Networks can then automatically learn across the graph to extract representations that leverage all input data, without any manual feature engineering. Relational Deep Learning leads to more accurate models that can be built much faster. To facilitate research in this area, we develop RelBench, a set of benchmark datasets and an implementation of Relational Deep Learning. The data covers a wide spectrum, from discussions on Stack Exchange to book reviews on the Amazon Product Catalog. Overall, we define a new research area that generalizes graph machine learning and broadens its applicability to a wide set of AI use cases.

Expressive Sign Equivariant Networks for Spectral Geometric Learning

Recent work has shown the utility of developing machine learning models that respect the structure and symmetries of eigenvectors. These works promote sign invariance, since for any eigenvector v the negation -v is also an eigenvector. However, we show that sign invariance is theoretically limited for tasks such as building orthogonally equivariant models and learning node positional encodings for link prediction in graphs. In this work, we demonstrate the benefits of sign equivariance for these tasks. To obtain these benefits, we develop novel sign equivariant neural network architectures. Our models are based on a new analytic characterization of sign equivariant polynomials and thus inherit provable expressiveness properties. Controlled synthetic experiments show that our networks can achieve the theoretically predicted benefits of sign equivariant models. Code is available at https://github.com/cptq/Sign-Equivariant-Nets.

On Retrieval Augmentation and the Limitations of Language Model Training

Augmenting a language model (LM) with $k$-nearest neighbors (kNN) retrieval on its training data alone can decrease its perplexity, though the underlying reasons for this remains elusive. In this work, we first rule out one previously posited possibility -- the "softmax bottleneck." We further identify the MLP hurdle phenomenon, where the final MLP layer in LMs may impede LM optimization early on. We explore memorization and generalization in language models with two new datasets, where advanced model like GPT-3.5-turbo find generalizing to irrelevant information in the training data challenging. However, incorporating kNN retrieval to vanilla GPT-2 117M can consistently improve performance in this setting.

On the Stability of Expressive Positional Encodings for Graph Neural Networks

Designing effective positional encodings for graphs is key to building powerful graph transformers and enhancing message-passing graph neural networks. Although widespread, using Laplacian eigenvectors as positional encodings faces two fundamental challenges: (1) \emph{Non-uniqueness}: there are many different eigendecompositions of the same Laplacian, and (2) \emph{Instability}: small perturbations to the Laplacian could result in completely different eigenspaces, leading to unpredictable changes in positional encoding. Despite many attempts to address non-uniqueness, most methods overlook stability, leading to poor generalization on unseen graph structures. We identify the cause of instability to be a "hard partition" of eigenspaces. Hence, we introduce Stable and Expressive Positional Encodings (SPE), an architecture for processing eigenvectors that uses eigenvalues to "softly partition" eigenspaces. SPE is the first architecture that is (1) provably stable, and (2) universally expressive for basis invariant functions whilst respecting all symmetries of eigenvectors. Besides guaranteed stability, we prove that SPE is at least as expressive as existing methods, and highly capable of counting graph structures. Finally, we evaluate the effectiveness of our method on molecular property prediction, and out-of-distribution generalization tasks, finding improved generalization compared to existing positional encoding methods.

Structuring Representation Geometry with Rotationally Equivariant Contrastive Learning

Self-supervised learning converts raw perceptual data such as images to a compact space where simple Euclidean distances measure meaningful variations in data. In this paper, we extend this formulation by adding additional geometric structure to the embedding space by enforcing transformations of input space to correspond to simple (i.e., linear) transformations of embedding space. Specifically, in the contrastive learning setting, we introduce an equivariance objective and theoretically prove that its minima forces augmentations on input space to correspond to rotations on the spherical embedding space. We show that merely combining our equivariant loss with a non-collapse term results in non-trivial representations, without requiring invariance to data augmentations. Optimal performance is achieved by also encouraging approximate invariance, where input augmentations correspond to small rotations. Our method, CARE: Contrastive Augmentation-induced Rotational Equivariance, leads to improved performance on downstream tasks, and ensures sensitivity in embedding space to important variations in data (e.g., color) that standard contrastive methods do not achieve. Code is available at https://github.com/Sharut/CARE.

A deep learning approach to using wearable seismocardiography for diagnosing aortic valve stenosis and predicting aortic hemodynamics obtained by 4D flow MRI

In this paper, we explored the use of deep learning for the prediction of aortic flow metrics obtained using 4D flow MRI using wearable seismocardiography (SCG) devices. 4D flow MRI provides a comprehensive assessment of cardiovascular hemodynamics, but it is costly and time-consuming. We hypothesized that deep learning could be used to identify pathological changes in blood flow, such as elevated peak systolic velocity Vmax in patients with heart valve diseases, from SCG signals. We also investigated the ability of this deep learning technique to differentiate between patients diagnosed with aortic valve stenosis (AS), non-AS patients with a bicuspid aortic valve (BAV), non-AS patients with a mechanical aortic valve (MAV), and healthy subjects with a normal tricuspid aortic valve (TAV). In a study of 77 subjects who underwent same-day 4D flow MRI and SCG, we found that the Vmax values obtained using deep learning and SCGs were in good agreement with those obtained by 4D flow MRI. Additionally, subjects with TAV, BAV, MAV, and AS could be classified with ROC-AUC values of 92%, 95%, 81%, and 83%, respectively. This suggests that SCG obtained using low-cost wearable electronics may be used as a supplement to 4D flow MRI exams or as a screening tool for aortic valve disease.

A simple, efficient and scalable contrastive masked autoencoder for learning visual representations

We introduce CAN, a simple, efficient and scalable method for self-supervised learning of visual representations. Our framework is a minimal and conceptually clean synthesis of (C) contrastive learning, (A) masked autoencoders, and (N) the noise prediction approach used in diffusion models. The learning mechanisms are complementary to one another: contrastive learning shapes the embedding space across a batch of image samples; masked autoencoders focus on reconstruction of the low-frequency spatial correlations in a single image sample; and noise prediction encourages the reconstruction of the high-frequency components of an image. The combined approach results in a robust, scalable and simple-to-implement algorithm. The training process is symmetric, with 50% of patches in both views being masked at random, yielding a considerable efficiency improvement over prior contrastive learning methods. Extensive empirical studies demonstrate that CAN achieves strong downstream performance under both linear and finetuning evaluations on transfer learning and robustness tasks. CAN outperforms MAE and SimCLR when pre-training on ImageNet, but is especially useful for pre-training on larger uncurated datasets such as JFT-300M: for linear probe on ImageNet, CAN achieves 75.4% compared to 73.4% for SimCLR and 64.1% for MAE. The finetuned performance on ImageNet of our ViT-L model is 86.1%, compared to 85.5% for SimCLR, and 85.4% for MAE. The overall FLOPs load of SimCLR is 70% higher than CAN for ViT-L models.

Neural Set Function Extensions: Learning with Discrete Functions in High Dimensions

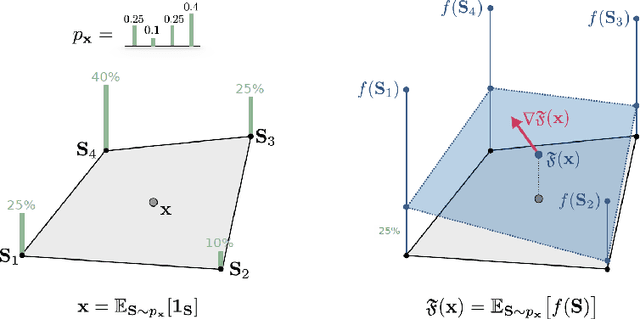
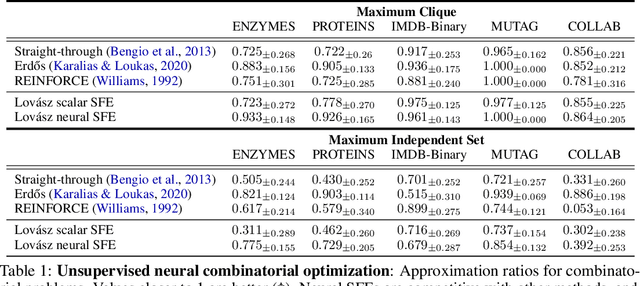
Integrating functions on discrete domains into neural networks is key to developing their capability to reason about discrete objects. But, discrete domains are (1) not naturally amenable to gradient-based optimization, and (2) incompatible with deep learning architectures that rely on representations in high-dimensional vector spaces. In this work, we address both difficulties for set functions, which capture many important discrete problems. First, we develop a framework for extending set functions onto low-dimensional continuous domains, where many extensions are naturally defined. Our framework subsumes many well-known extensions as special cases. Second, to avoid undesirable low-dimensional neural network bottlenecks, we convert low-dimensional extensions into representations in high-dimensional spaces, taking inspiration from the success of semidefinite programs for combinatorial optimization. Empirically, we observe benefits of our extensions for unsupervised neural combinatorial optimization, in particular with high-dimensional representations.