Are Graph Neural Networks Optimal Approximation Algorithms?

In this work we design graph neural network architectures that can be used to obtain optimal approximation algorithms for a large class of combinatorial optimization problems using powerful algorithmic tools from semidefinite programming (SDP). Concretely, we prove that polynomial-sized message passing algorithms can represent the most powerful polynomial time algorithms for Max Constraint Satisfaction Problems assuming the Unique Games Conjecture. We leverage this result to construct efficient graph neural network architectures, OptGNN, that obtain high-quality approximate solutions on landmark combinatorial optimization problems such as Max Cut and maximum independent set. Our approach achieves strong empirical results across a wide range of real-world and synthetic datasets against both neural baselines and classical algorithms. Finally, we take advantage of OptGNN's ability to capture convex relaxations to design an algorithm for producing dual certificates of optimality (bounds on the optimal solution) from the learned embeddings of OptGNN.

Neural Set Function Extensions: Learning with Discrete Functions in High Dimensions

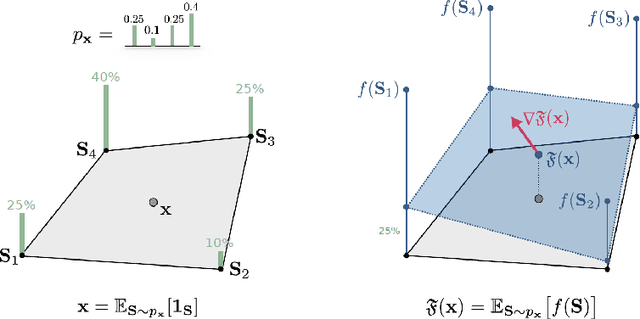
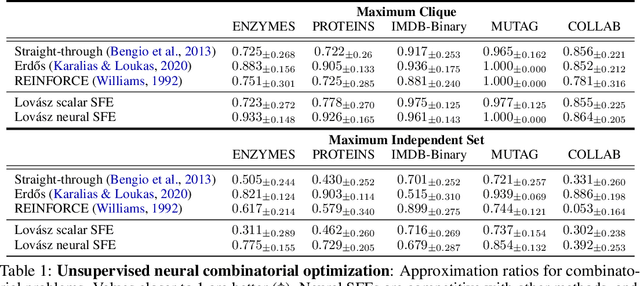
Integrating functions on discrete domains into neural networks is key to developing their capability to reason about discrete objects. But, discrete domains are (1) not naturally amenable to gradient-based optimization, and (2) incompatible with deep learning architectures that rely on representations in high-dimensional vector spaces. In this work, we address both difficulties for set functions, which capture many important discrete problems. First, we develop a framework for extending set functions onto low-dimensional continuous domains, where many extensions are naturally defined. Our framework subsumes many well-known extensions as special cases. Second, to avoid undesirable low-dimensional neural network bottlenecks, we convert low-dimensional extensions into representations in high-dimensional spaces, taking inspiration from the success of semidefinite programs for combinatorial optimization. Empirically, we observe benefits of our extensions for unsupervised neural combinatorial optimization, in particular with high-dimensional representations.

Partition and Code: learning how to compress graphs

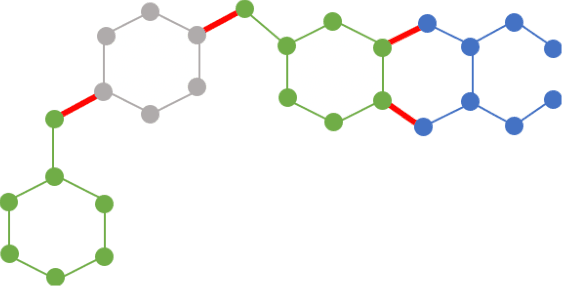
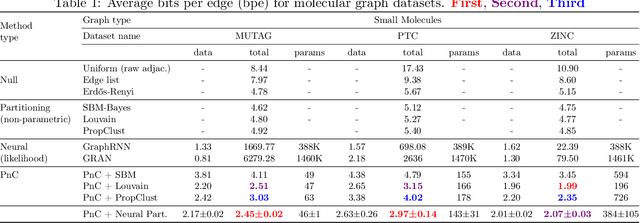
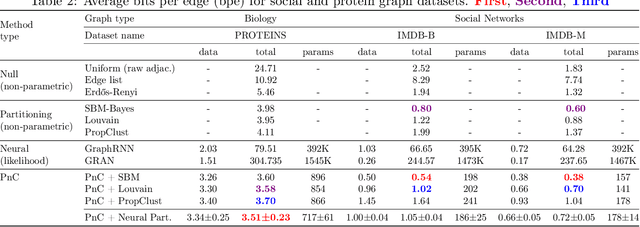
Can we use machine learning to compress graph data? The absence of ordering in graphs poses a significant challenge to conventional compression algorithms, limiting their attainable gains as well as their ability to discover relevant patterns. On the other hand, most graph compression approaches rely on domain-dependent handcrafted representations and cannot adapt to different underlying graph distributions. This work aims to establish the necessary principles a lossless graph compression method should follow to approach the entropy storage lower bound. Instead of making rigid assumptions about the graph distribution, we formulate the compressor as a probabilistic model that can be learned from data and generalise to unseen instances. Our "Partition and Code" framework entails three steps: first, a partitioning algorithm decomposes the graph into elementary structures, then these are mapped to the elements of a small dictionary on which we learn a probability distribution, and finally, an entropy encoder translates the representation into bits. All three steps are parametric and can be trained with gradient descent. We theoretically compare the compression quality of several graph encodings and prove, under mild conditions, a total ordering of their expected description lengths. Moreover, we show that, under the same conditions, PnC achieves compression gains w.r.t. the baselines that grow either linearly or quadratically with the number of vertices. Our algorithms are quantitatively evaluated on diverse real-world networks obtaining significant performance improvements with respect to different families of non-parametric and parametric graph compressors.

Erdos Goes Neural: an Unsupervised Learning Framework for Combinatorial Optimization on Graphs

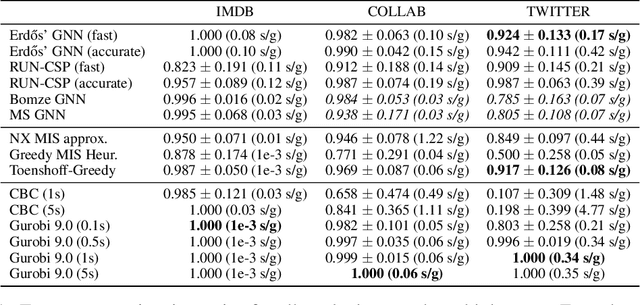
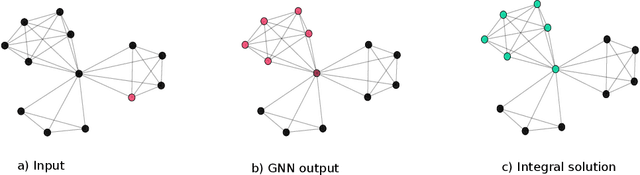
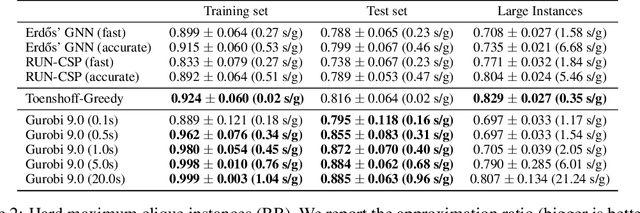
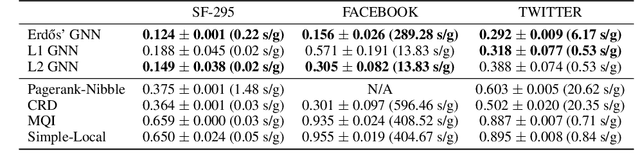
Combinatorial optimization problems are notoriously challenging for neural networks, especially in the absence of labeled instances. This work proposes an unsupervised learning framework for CO problems on graphs that can provide integral solutions of certified quality. Inspired by Erdos' probabilistic method, we use a neural network to parametrize a probability distribution over sets. Crucially, we show that when the network is optimized w.r.t. a suitably chosen loss, the learned distribution contains, with controlled probability, a low-cost integral solution that obeys the constraints of the combinatorial problem. The probabilistic proof of existence is then derandomized to decode the desired solutions. We demonstrate the efficacy of this approach to obtain valid solutions to the maximum clique problem and to perform local graph clustering. Our method achieves competitive results on both real datasets and synthetic hard instances.