Non-Asymptotic Error Bounds for Bidirectional GANs

We derive nearly sharp bounds for the bidirectional GAN (BiGAN) estimation error under the Dudley distance between the latent joint distribution and the data joint distribution with appropriately specified architecture of the neural networks used in the model. To the best of our knowledge, this is the first theoretical guarantee for the bidirectional GAN learning approach. An appealing feature of our results is that they do not assume the reference and the data distributions to have the same dimensions or these distributions to have bounded support. These assumptions are commonly assumed in the existing convergence analysis of the unidirectional GANs but may not be satisfied in practice. Our results are also applicable to the Wasserstein bidirectional GAN if the target distribution is assumed to have a bounded support. To prove these results, we construct neural network functions that push forward an empirical distribution to another arbitrary empirical distribution on a possibly different-dimensional space. We also develop a novel decomposition of the integral probability metric for the error analysis of bidirectional GANs. These basic theoretical results are of independent interest and can be applied to other related learning problems.

A Learning-based Approach Towards Automated Tuning of SSD Configurations

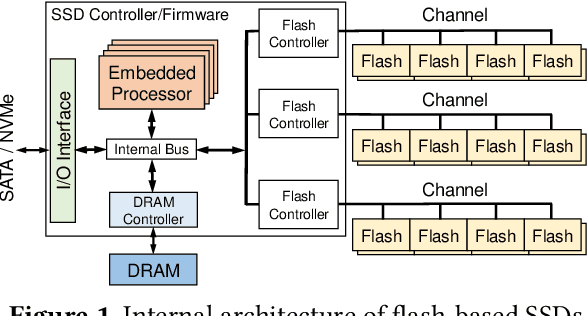
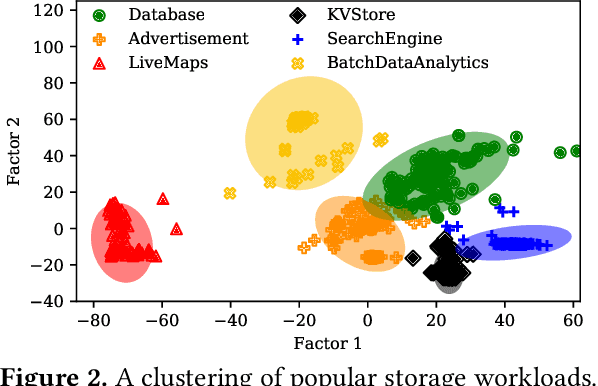
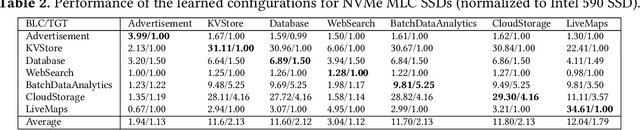
Thanks to the mature manufacturing techniques, solid-state drives (SSDs) are highly customizable for applications today, which brings opportunities to further improve their storage performance and resource utilization. However, the SSD efficiency is usually determined by many hardware parameters, making it hard for developers to manually tune them and determine the optimal SSD configurations. In this paper, we present an automated learning-based framework, named LearnedSSD, that utilizes both supervised and unsupervised machine learning (ML) techniques to drive the tuning of hardware configurations for SSDs. LearnedSSD automatically extracts the unique access patterns of a new workload using its block I/O traces, maps the workload to previously workloads for utilizing the learned experiences, and recommends an optimal SSD configuration based on the validated storage performance. LearnedSSD accelerates the development of new SSD devices by automating the hard-ware parameter configurations and reducing the manual efforts. We develop LearnedSSD with simple yet effective learning algorithms that can run efficiently on multi-core CPUs. Given a target storage workload, our evaluation shows that LearnedSSD can always deliver an optimal SSD configuration for the target workload, and this configuration will not hurt the performance of non-target workloads.

Relative Entropy Gradient Sampler for Unnormalized Distributions

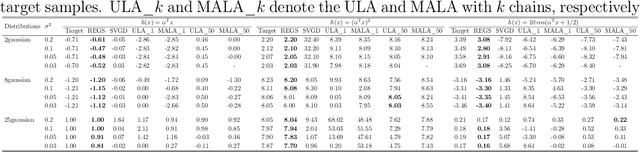
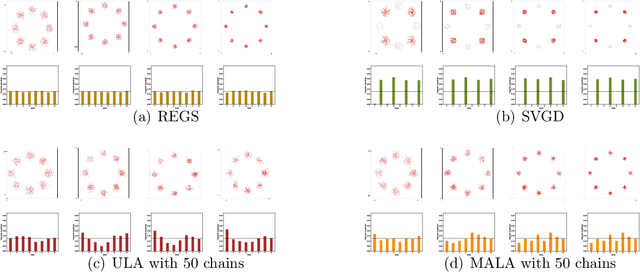
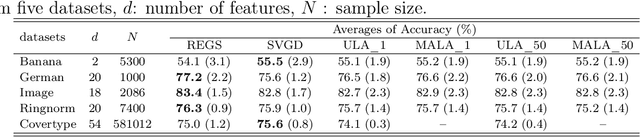
We propose a relative entropy gradient sampler (REGS) for sampling from unnormalized distributions. REGS is a particle method that seeks a sequence of simple nonlinear transforms iteratively pushing the initial samples from a reference distribution into the samples from an unnormalized target distribution. To determine the nonlinear transforms at each iteration, we consider the Wasserstein gradient flow of relative entropy. This gradient flow determines a path of probability distributions that interpolates the reference distribution and the target distribution. It is characterized by an ODE system with velocity fields depending on the density ratios of the density of evolving particles and the unnormalized target density. To sample with REGS, we need to estimate the density ratios and simulate the ODE system with particle evolution. We propose a novel nonparametric approach to estimating the logarithmic density ratio using neural networks. Extensive simulation studies on challenging multimodal 1D and 2D mixture distributions and Bayesian logistic regression on real datasets demonstrate that the REGS outperforms the state-of-the-art sampling methods included in the comparison.

An error analysis of generative adversarial networks for learning distributions

This paper studies how well generative adversarial networks (GANs) learn probability distributions from finite samples. Our main results establish the convergence rates of GANs under a collection of integral probability metrics defined through H\"older classes, including the Wasserstein distance as a special case. We also show that GANs are able to adaptively learn data distributions with low-dimensional structures or have H\"older densities, when the network architectures are chosen properly. In particular, for distributions concentrated around a low-dimensional set, we show that the learning rates of GANs do not depend on the high ambient dimension, but on the lower intrinsic dimension. Our analysis is based on a new oracle inequality decomposing the estimation error into the generator and discriminator approximation error and the statistical error, which may be of independent interest.

Non-asymptotic Excess Risk Bounds for Classification with Deep Convolutional Neural Networks

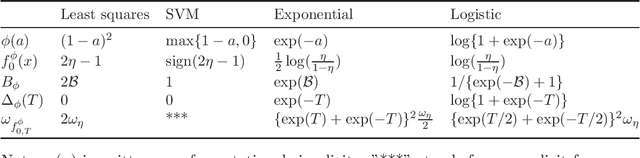
In this paper, we consider the problem of binary classification with a class of general deep convolutional neural networks, which includes fully-connected neural networks and fully convolutional neural networks as special cases. We establish non-asymptotic excess risk bounds for a class of convex surrogate losses and target functions with different modulus of continuity. An important feature of our results is that we clearly define the prefactors of the risk bounds in terms of the input data dimension and other model parameters and show that they depend polynomially on the dimensionality in some important models. We also show that the classification methods with CNNs can circumvent the curse of dimensionality if the input data is supported on an approximate low-dimensional manifold. To establish these results, we derive an upper bound for the covering number for the class of general convolutional neural networks with a bias term in each convolutional layer, and derive new results on the approximation power of CNNs for any uniformly-continuous target functions. These results provide further insights into the complexity and the approximation power of general convolutional neural networks, which are of independent interest and may have other applications. Finally, we apply our general results to analyze the non-asymptotic excess risk bounds for four widely used methods with different loss functions using CNNs, including the least squares, the logistic, the exponential and the SVM hinge losses.

Natural grasp intention recognition based on gaze fixation in human-robot interaction

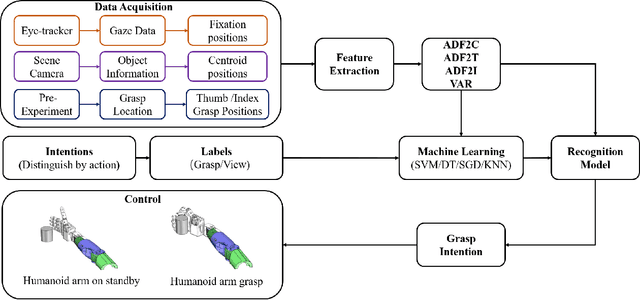
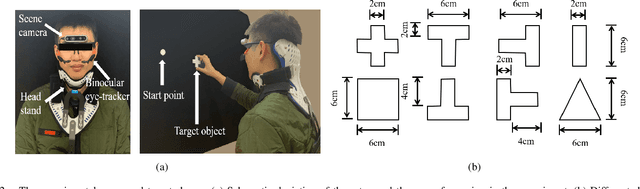
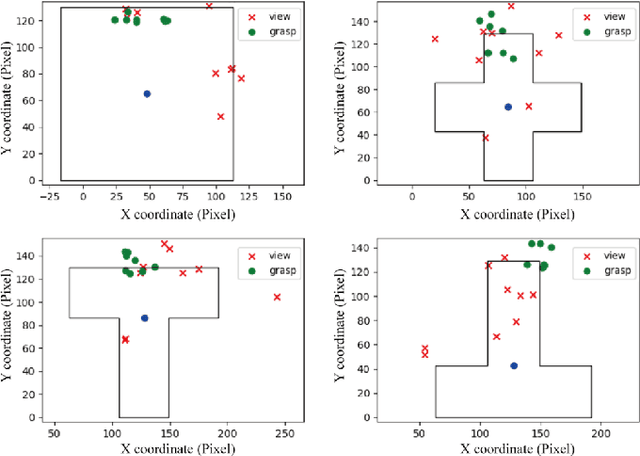
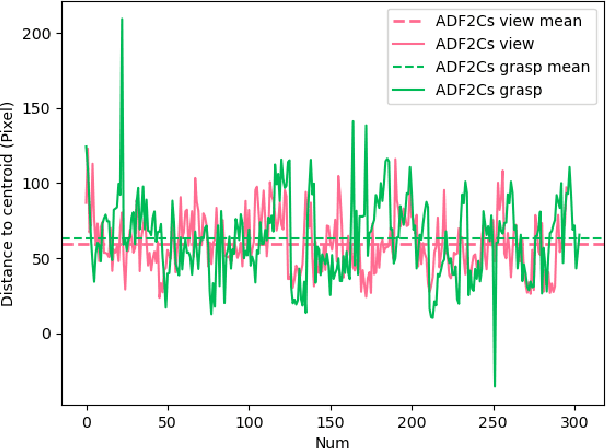
Eye movement is closely related to limb actions, so it can be used to infer movement intentions. More importantly, in some cases, eye movement is the only way for paralyzed and impaired patients with severe movement disorders to communicate and interact with the environment. Despite this, eye-tracking technology still has very limited application scenarios as an intention recognition method. The goal of this paper is to achieve a natural fixation-based grasping intention recognition method, with which a user with hand movement disorders can intuitively express what tasks he/she wants to do by directly looking at the object of interest. Toward this goal, we design experiments to study the relationships of fixations in different tasks. We propose some quantitative features from these relationships and analyze them statistically. Then we design a natural method for grasping intention recognition. The experimental results prove that the accuracy of the proposed method for the grasping intention recognition exceeds 89\% on the training objects. When this method is extendedly applied to objects not included in the training set, the average accuracy exceeds 85\%. The grasping experiment in the actual environment verifies the effectiveness of the proposed method.

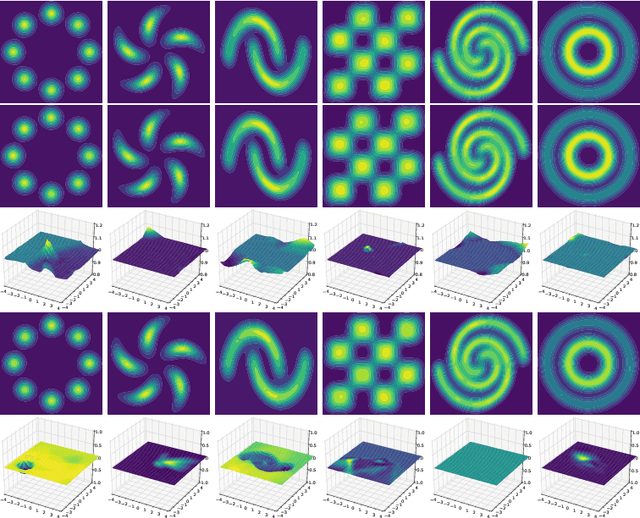
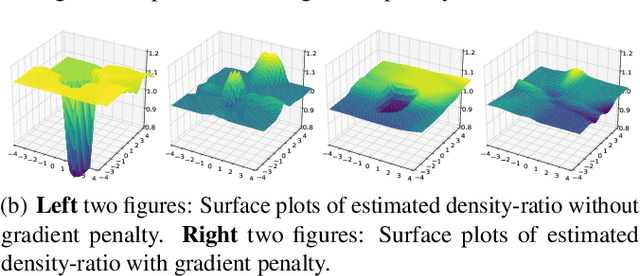
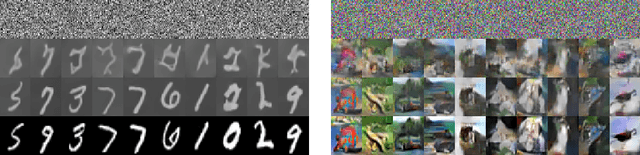
Generative Learning With Euler Particle Transport

We propose an Euler particle transport (EPT) approach for generative learning. The proposed approach is motivated by the problem of finding an optimal transport map from a reference distribution to a target distribution characterized by the Monge-Ampere equation. Interpreting the infinitesimal linearization of the Monge-Ampere equation from the perspective of gradient flows in measure spaces leads to a stochastic McKean-Vlasov equation. We use the forward Euler method to solve this equation. The resulting forward Euler map pushes forward a reference distribution to the target. This map is the composition of a sequence of simple residual maps, which are computationally stable and easy to train. The key task in training is the estimation of the density ratios or differences that determine the residual maps. We estimate the density ratios (differences) based on the Bregman divergence with a gradient penalty using deep density-ratio (difference) fitting. We show that the proposed density-ratio (difference) estimators do not suffer from the "curse of dimensionality" if data is supported on a lower-dimensional manifold. Numerical experiments with multi-mode synthetic datasets and comparisons with the existing methods on real benchmark datasets support our theoretical results and demonstrate the effectiveness of the proposed method.

EEG-Based Brain-Computer Interfaces Are Vulnerable to Backdoor Attacks

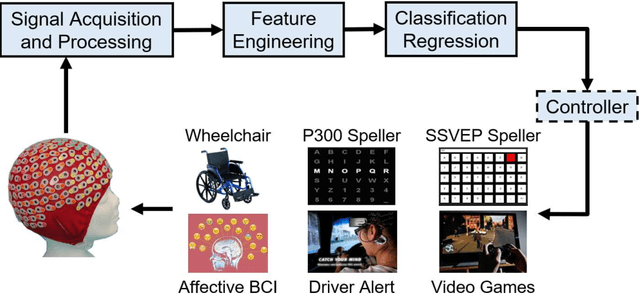
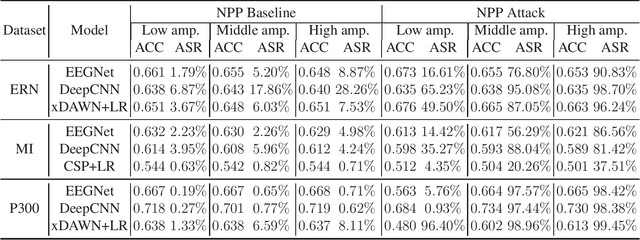
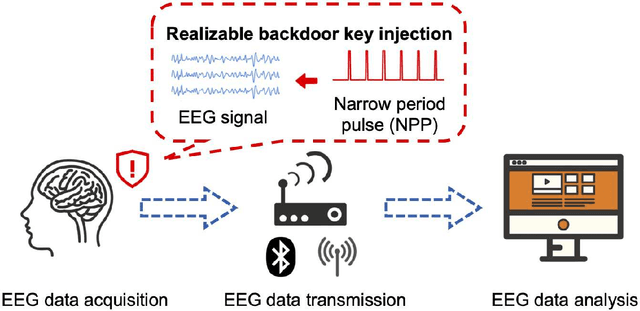
Research and development of electroencephalogram (EEG) based brain-computer interfaces (BCIs) have advanced rapidly, partly due to the wide adoption of sophisticated machine learning approaches for decoding the EEG signals. However, recent studies have shown that machine learning algorithms are vulnerable to adversarial attacks, e.g., the attacker can add tiny adversarial perturbations to a test sample to fool the model, or poison the training data to insert a secret backdoor. Previous research has shown that adversarial attacks are also possible for EEG-based BCIs. However, only adversarial perturbations have been considered, and the approaches are theoretically sound but very difficult to implement in practice. This article proposes to use narrow period pulse for poisoning attack of EEG-based BCIs, which is more feasible in practice and has never been considered before. One can create dangerous backdoors in the machine learning model by injecting poisoning samples into the training set. Test samples with the backdoor key will then be classified into the target class specified by the attacker. What most distinguishes our approach from previous ones is that the backdoor key does not need to be synchronized with the EEG trials, making it very easy to implement. The effectiveness and robustness of the backdoor attack approach is demonstrated, highlighting a critical security concern for EEG-based BCIs.

Transfer Learning for Brain-Computer Interfaces: A Complete Pipeline

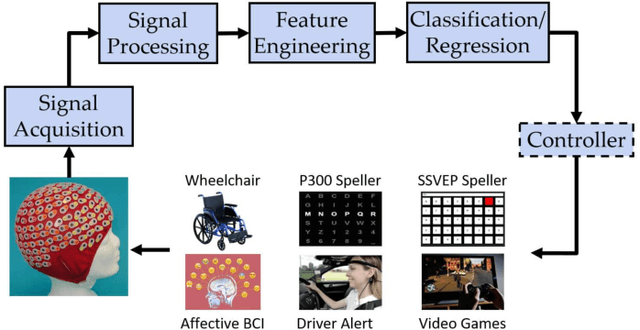
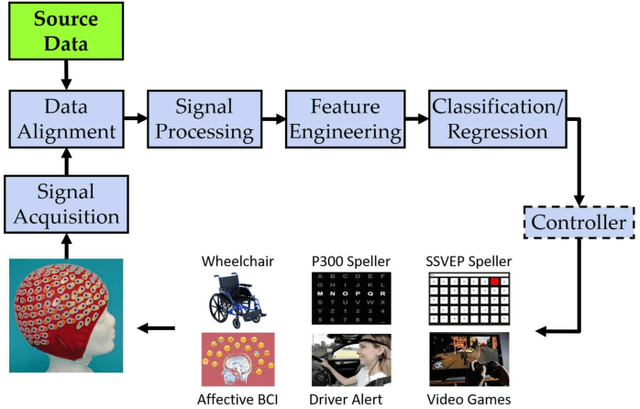
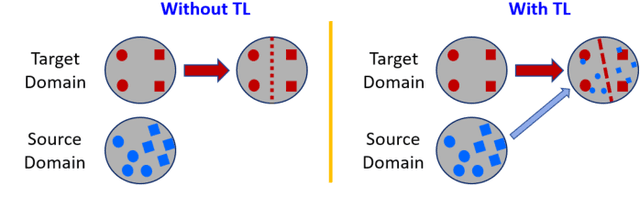
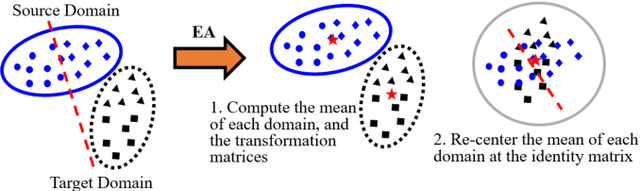
Transfer learning (TL) has been widely used in electroencephalogram (EEG) based brain-computer interfaces (BCIs) to reduce the calibration effort for a new subject, and demonstrated promising performance. After EEG signal acquisition, a closed-loop EEG-based BCI system also includes signal processing, feature engineering, and classification/regression blocks before sending out the control signal, whereas previous approaches only considered TL in one or two such components. This paper proposes that TL could be considered in all three components (signal processing, feature engineering, and classification/regression). Furthermore, it is also very important to specifically add a data alignment component before signal processing to make the data from different subjects more consistent, and hence to facilitate subsequential TL. Offline calibration experiments on two MI datasets verified our proposal. Especially, integrating data alignment and sophisticated TL approaches can significantly improve the classification performance, and hence greatly reduce the calibration effort.

Deep Dimension Reduction for Supervised Representation Learning

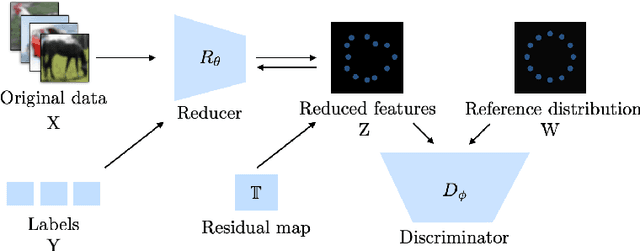
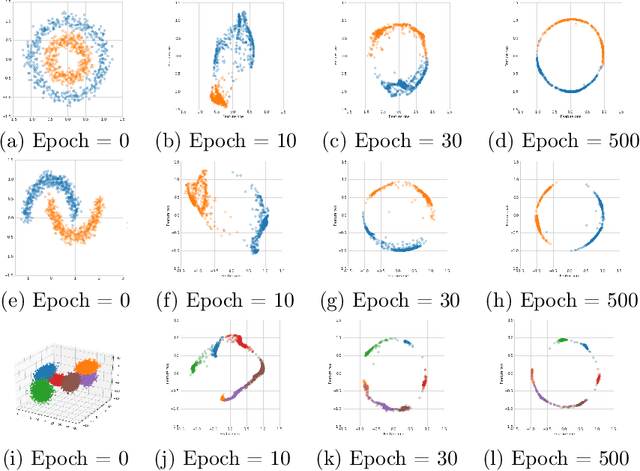
The success of deep supervised learning depends on its automatic data representation abilities. Among all the characteristics of an ideal representation for high-dimensional complex data, information preservation, low dimensionality and disentanglement are the most essential ones. In this work, we propose a deep dimension reduction (DDR) approach to achieving a good data representation with these characteristics for supervised learning. At the population level, we formulate the ideal representation learning task as finding a nonlinear dimension reduction map that minimizes the sum of losses characterizing conditional independence and disentanglement. We estimate the target map at the sample level nonparametrically with deep neural networks. We derive a bound on the excess risk of the deep nonparametric estimator. The proposed method is validated via comprehensive numerical experiments and real data analysis in the context of regression and classification.