ABot-AgentOS: A General Robotic Agent OS with Lifelong Multi-modal Memory

Recent VLM and VLA systems have improved robotic perception and action prediction, yet long-horizon embodied agents still require a general runtime layer for reasoning, memory, tool use, verification, and cross-embodiment execution. We present ABot-AgentOS, a general robotic Agent Operating System that sits above low-level controllers and provides a deliberative agent layer for scene-conditioned planning, context-isolated skill execution, multi-stage verification, multi-modal memory, and edge-cloud collaboration. To evaluate such systems, we introduce EmbodiedWorldBench, an executable benchmark with 16 indoor, outdoor, and hybrid scenes, four difficulty levels, and over 200 tasks involving navigation, object search, NPC dialogue, dynamic events, and trace-grounded scoring. ABot-AgentOS further introduces Universal Multi-modal Graph Memory, a persistent source-grounded substrate that converts dialogue, visual observations, spatial context, temporal relations, and task traces into typed nodes and edges. A failure-driven self-evolution loop converts diagnosed memory failures into gated runtime evo-assets that are promoted only to later evaluation splits, preventing current-split ground-truth leakage while enabling continual improvement. On an initial EmbodiedWorldBench subset, ABot-AgentOS improves over a single-controller baseline in both task success and goal completion. Across memory benchmarks, ABot-AgentOS Static achieves 87.5 on LoCoMo, 59.9 on OpenEQA EM-EQA, 88.6 on Mem-Gallery, and 76.5 Acc@All on NExT-QA; self-evolution further improves LoCoMo to 88.7, OpenEQA to 60.4, and Mem-Gallery to 89.0. These results suggest that a general Agent OS layer can improve long-horizon embodied execution while providing persistent, auditable memory for continual interaction.

Wasserstein Generative Learning of Conditional Distribution

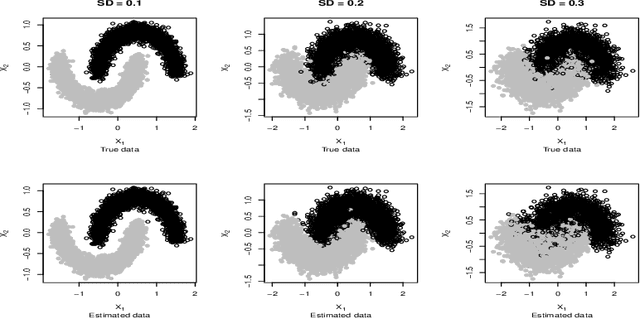
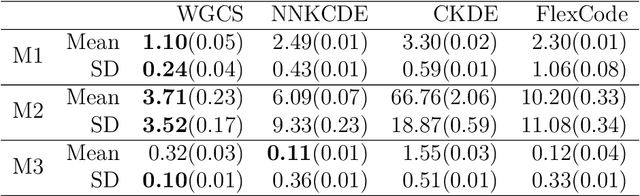
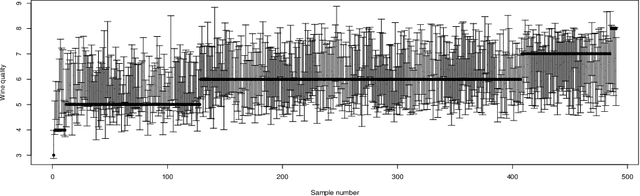
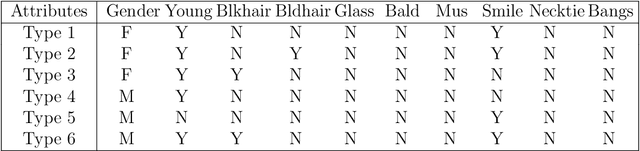
Conditional distribution is a fundamental quantity for describing the relationship between a response and a predictor. We propose a Wasserstein generative approach to learning a conditional distribution. The proposed approach uses a conditional generator to transform a known distribution to the target conditional distribution. The conditional generator is estimated by matching a joint distribution involving the conditional generator and the target joint distribution, using the Wasserstein distance as the discrepancy measure for these joint distributions. We establish non-asymptotic error bound of the conditional sampling distribution generated by the proposed method and show that it is able to mitigate the curse of dimensionality, assuming that the data distribution is supported on a lower-dimensional set. We conduct numerical experiments to validate proposed method and illustrate its applications to conditional sample generation, nonparametric conditional density estimation, prediction uncertainty quantification, bivariate response data, image reconstruction and image generation.

Non-Asymptotic Error Bounds for Bidirectional GANs

We derive nearly sharp bounds for the bidirectional GAN (BiGAN) estimation error under the Dudley distance between the latent joint distribution and the data joint distribution with appropriately specified architecture of the neural networks used in the model. To the best of our knowledge, this is the first theoretical guarantee for the bidirectional GAN learning approach. An appealing feature of our results is that they do not assume the reference and the data distributions to have the same dimensions or these distributions to have bounded support. These assumptions are commonly assumed in the existing convergence analysis of the unidirectional GANs but may not be satisfied in practice. Our results are also applicable to the Wasserstein bidirectional GAN if the target distribution is assumed to have a bounded support. To prove these results, we construct neural network functions that push forward an empirical distribution to another arbitrary empirical distribution on a possibly different-dimensional space. We also develop a novel decomposition of the integral probability metric for the error analysis of bidirectional GANs. These basic theoretical results are of independent interest and can be applied to other related learning problems.

An error analysis of generative adversarial networks for learning distributions

This paper studies how well generative adversarial networks (GANs) learn probability distributions from finite samples. Our main results establish the convergence rates of GANs under a collection of integral probability metrics defined through H\"older classes, including the Wasserstein distance as a special case. We also show that GANs are able to adaptively learn data distributions with low-dimensional structures or have H\"older densities, when the network architectures are chosen properly. In particular, for distributions concentrated around a low-dimensional set, we show that the learning rates of GANs do not depend on the high ambient dimension, but on the lower intrinsic dimension. Our analysis is based on a new oracle inequality decomposing the estimation error into the generator and discriminator approximation error and the statistical error, which may be of independent interest.