Hierarchical Policy Blending as Inference for Reactive Robot Control

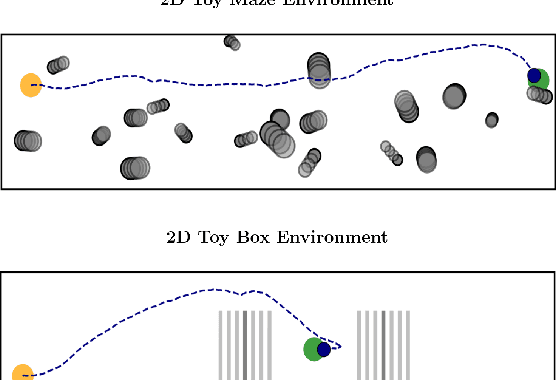
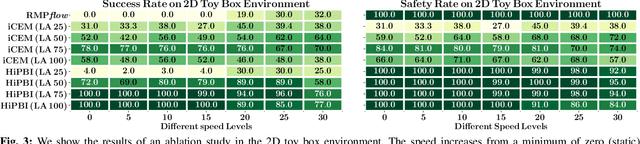
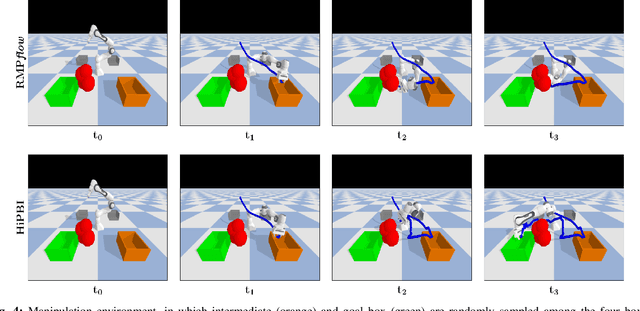
Motion generation in cluttered, dense, and dynamic environments is a central topic in robotics, rendered as a multi-objective decision-making problem. Current approaches trade-off between safety and performance. On the one hand, reactive policies guarantee fast response to environmental changes at the risk of suboptimal behavior. On the other hand, planning-based motion generation provides feasible trajectories, but the high computational cost may limit the control frequency and thus safety. To combine the benefits of reactive policies and planning, we propose a hierarchical motion generation method. Moreover, we adopt probabilistic inference methods to formalize the hierarchical model and stochastic optimization. We realize this approach as a weighted product of stochastic, reactive expert policies, where planning is used to adaptively compute the optimal weights over the task horizon. This stochastic optimization avoids local optima and proposes feasible reactive plans that find paths in cluttered and dense environments. Our extensive experimental study in planar navigation and 6DoF manipulation shows that our proposed hierarchical motion generation method outperforms both myopic reactive controllers and online re-planning methods.

Inferring Smooth Control: Monte Carlo Posterior Policy Iteration with Gaussian Processes

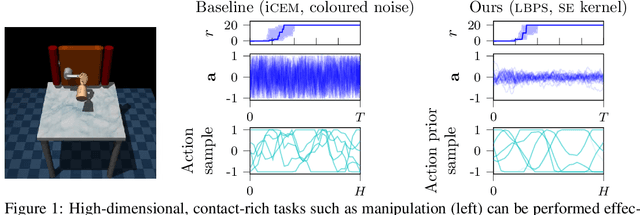
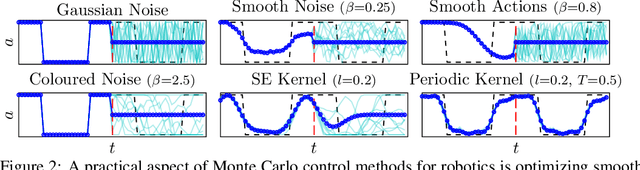
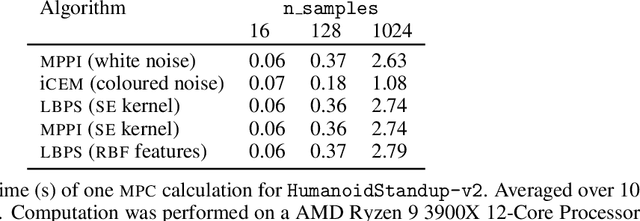
Monte Carlo methods have become increasingly relevant for control of non-differentiable systems, approximate dynamics models and learning from data. These methods scale to high-dimensional spaces and are effective at the non-convex optimizations often seen in robot learning. We look at sample-based methods from the perspective of inference-based control, specifically posterior policy iteration. From this perspective, we highlight how Gaussian noise priors produce rough control actions that are unsuitable for physical robot deployment. Considering smoother Gaussian process priors, as used in episodic reinforcement learning and motion planning, we demonstrate how smoother model predictive control can be achieved using online sequential inference. This inference is realized through an efficient factorization of the action distribution and a novel means of optimizing the likelihood temperature to improve importance sampling accuracy. We evaluate this approach on several high-dimensional robot control tasks, matching the sample efficiency of prior heuristic methods while also ensuring smoothness. Simulation results can be seen at https://monte-carlo-ppi.github.io/.

Placing by Touching: An empirical study on the importance of tactile sensing for precise object placing

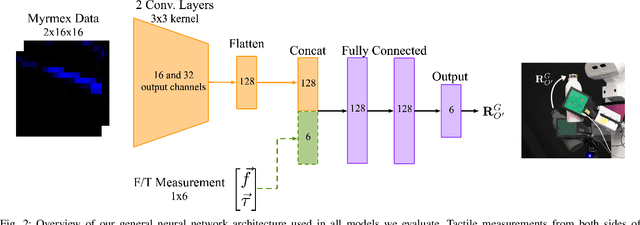
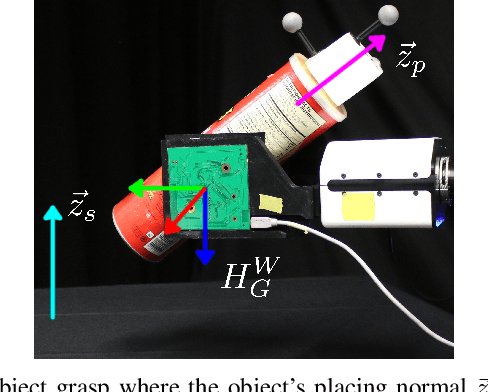
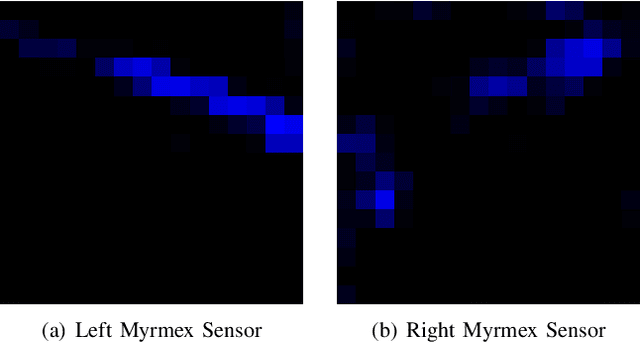
Tactile sensors are promising tools for endowing robots with embodied intelligence and increased dexterity. These sensors can provide robotic systems with direct information about physical interactions with the world, which is difficult to obtain from extrinsic perception systems. This work deals with a practical everyday living problem: stable object placement on flat surfaces starting from unknown initial poses. Common approaches for object placing either require complete scene specifications or indirect sensor measurements, such as cameras which are prone to suffer from occlusions. Instead, this work proposes a novel approach for stable object placing that combines tactile feedback and proprioceptive sensing. We devise a neural architecture that estimates a rotation matrix which results in a corrective gripper movement that aligns the object with the table and paves the way for the subsequent stable object placement. We compare models with different sensing modalities, such as force-torque and an external motion capture system, in real-world object placement tasks with different objects. Our experimental evaluation of the placing policies with a set of unknown everyday objects reveals an impressive generalization of the tactile-based pipeline and suggests that tactile sensing plays a vital role in the intrinsic understanding of dexterous object manipulation. Videos of our approach are available at https://sites.google.com/view/placing-by-touching.

Safe reinforcement learning of dynamic high-dimensional robotic tasks: navigation, manipulation, interaction

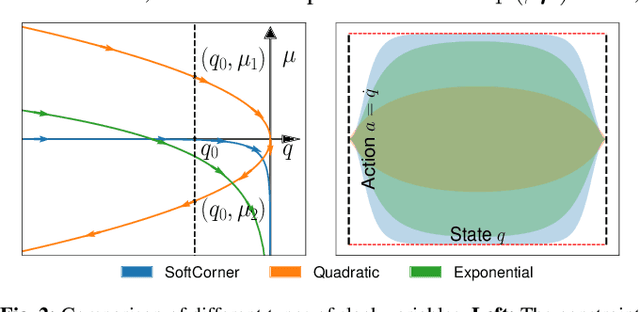
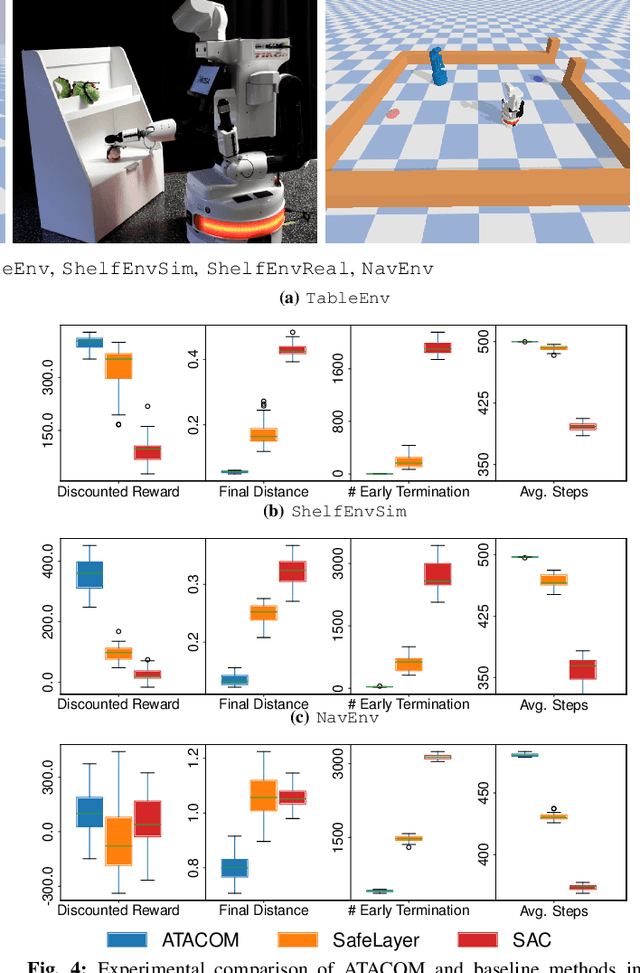
Safety is a crucial property of every robotic platform: any control policy should always comply with actuator limits and avoid collisions with the environment and humans. In reinforcement learning, safety is even more fundamental for exploring an environment without causing any damage. While there are many proposed solutions to the safe exploration problem, only a few of them can deal with the complexity of the real world. This paper introduces a new formulation of safe exploration for reinforcement learning of various robotic tasks. Our approach applies to a wide class of robotic platforms and enforces safety even under complex collision constraints learned from data by exploring the tangent space of the constraint manifold. Our proposed approach achieves state-of-the-art performance in simulated high-dimensional and dynamic tasks while avoiding collisions with the environment. We show safe real-world deployment of our learned controller on a TIAGo++ robot, achieving remarkable performance in manipulation and human-robot interaction tasks.

SE(3)-DiffusionFields: Learning smooth cost functions for joint grasp and motion optimization through diffusion

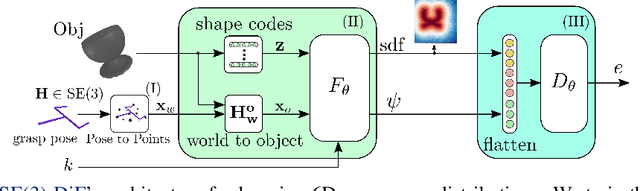
Multi-objective optimization problems are ubiquitous in robotics, e.g., the optimization of a robot manipulation task requires a joint consideration of grasp pose configurations, collisions and joint limits. While some demands can be easily hand-designed, e.g., the smoothness of a trajectory, several task-specific objectives need to be learned from data. This work introduces a method for learning data-driven SE(3) cost functions as diffusion models. Diffusion models can represent highly-expressive multimodal distributions and exhibit proper gradients over the entire space due to their score-matching training objective. Learning costs as diffusion models allows their seamless integration with other costs into a single differentiable objective function, enabling joint gradient-based motion optimization. In this work, we focus on learning SE(3) diffusion models for 6DoF grasping, giving rise to a novel framework for joint grasp and motion optimization without needing to decouple grasp selection from trajectory generation. We evaluate the representation power of our SE(3) diffusion models w.r.t. classical generative models, and we showcase the superior performance of our proposed optimization framework in a series of simulated and real-world robotic manipulation tasks against representative baselines.

Structured Q-learning For Antibody Design

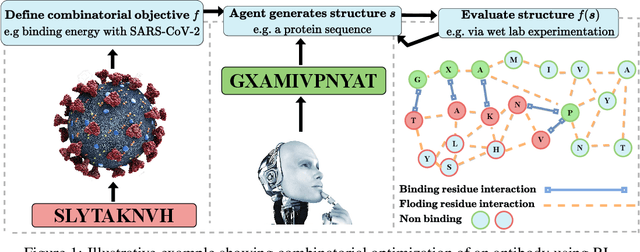
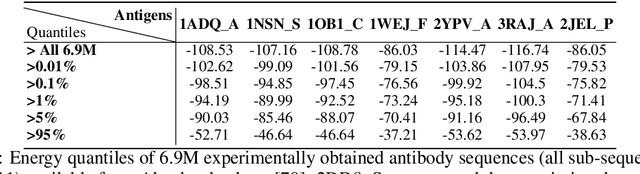
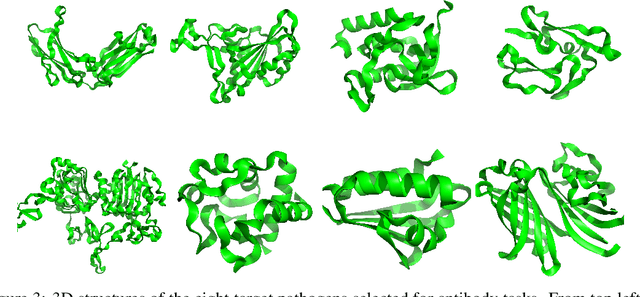
Optimizing combinatorial structures is core to many real-world problems, such as those encountered in life sciences. For example, one of the crucial steps involved in antibody design is to find an arrangement of amino acids in a protein sequence that improves its binding with a pathogen. Combinatorial optimization of antibodies is difficult due to extremely large search spaces and non-linear objectives. Even for modest antibody design problems, where proteins have a sequence length of eleven, we are faced with searching over 2.05 x 10^14 structures. Applying traditional Reinforcement Learning algorithms such as Q-learning to combinatorial optimization results in poor performance. We propose Structured Q-learning (SQL), an extension of Q-learning that incorporates structural priors for combinatorial optimization. Using a molecular docking simulator, we demonstrate that SQL finds high binding energy sequences and performs favourably against baselines on eight challenging antibody design tasks, including designing antibodies for SARS-COV.

Self-supervised Sequential Information Bottleneck for Robust Exploration in Deep Reinforcement Learning

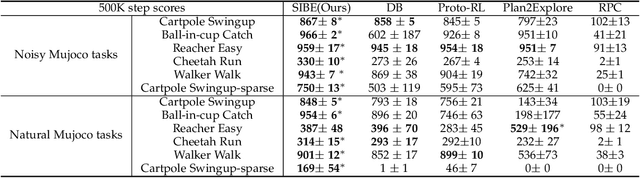
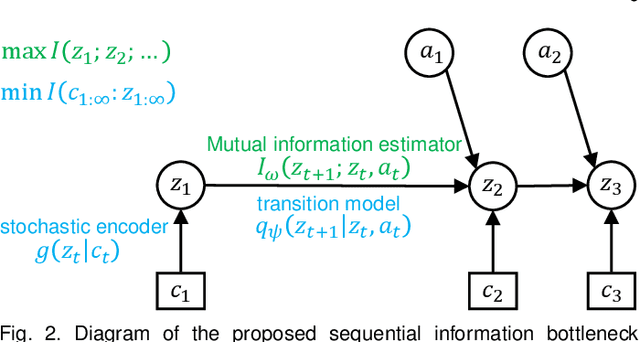
Effective exploration is critical for reinforcement learning agents in environments with sparse rewards or high-dimensional state-action spaces. Recent works based on state-visitation counts, curiosity and entropy-maximization generate intrinsic reward signals to motivate the agent to visit novel states for exploration. However, the agent can get distracted by perturbations to sensor inputs that contain novel but task-irrelevant information, e.g. due to sensor noise or changing background. In this work, we introduce the sequential information bottleneck objective for learning compressed and temporally coherent representations by modelling and compressing sequential predictive information in time-series observations. For efficient exploration in noisy environments, we further construct intrinsic rewards that capture task-relevant state novelty based on the learned representations. We derive a variational upper bound of our sequential information bottleneck objective for practical optimization and provide an information-theoretic interpretation of the derived upper bound. Our experiments on a set of challenging image-based simulated control tasks show that our method achieves better sample efficiency, and robustness to both white noise and natural video backgrounds compared to state-of-art methods based on curiosity, entropy maximization and information-gain.

Controlling the Cascade: Kinematic Planning for N-ball Toss Juggling

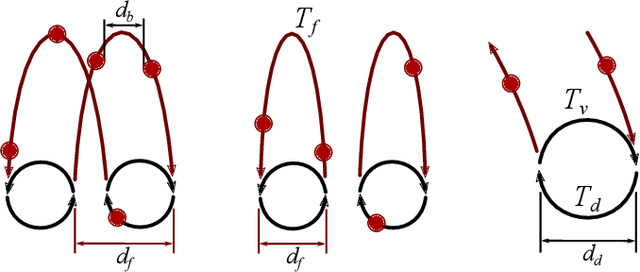
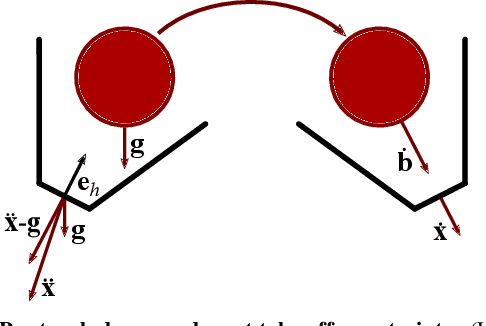
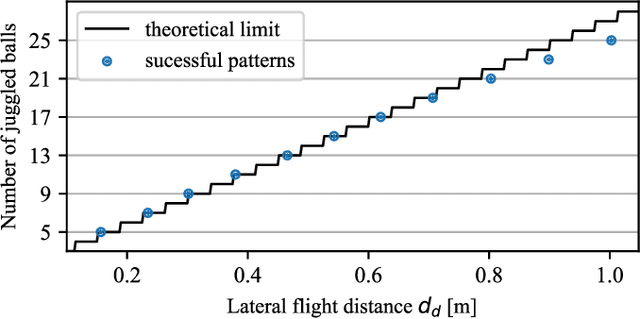
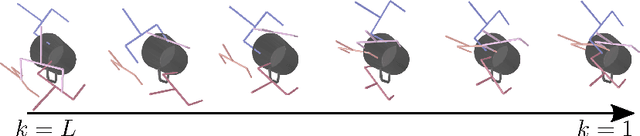
Dynamic movements are ubiquitous in human motor behavior as they tend to be more efficient and can solve a broader range of skill domains than their quasi-static counterparts. For decades, robotic juggling tasks have been among the most frequently studied dynamic manipulation problems since the required dynamic dexterity can be scaled to arbitrarily high difficulty. However, successful approaches have been limited to basic juggling skills, indicating a lack of understanding of the required constraints for dexterous toss juggling. We present a detailed analysis of the toss juggling task, identifying the key challenges and formalizing it as a trajectory optimization problem. Building on our state-of-the-art, real-world toss juggling platform, we reach the theoretical limits of toss juggling in simulation, evaluate a resulting real-time controller in environments of varying difficulty and achieve robust toss juggling of up to 17 balls on two anthropomorphic manipulators.

Learning Implicit Priors for Motion Optimization

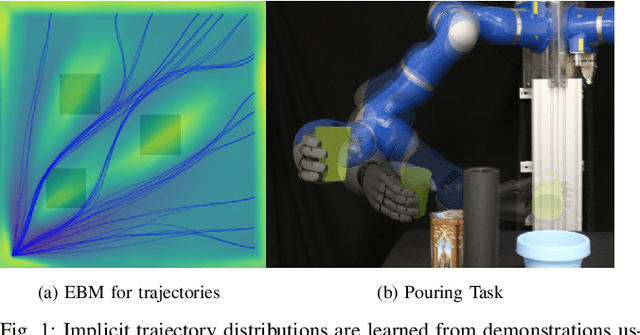
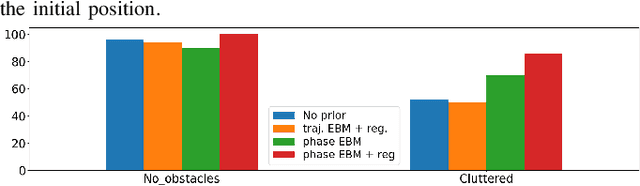
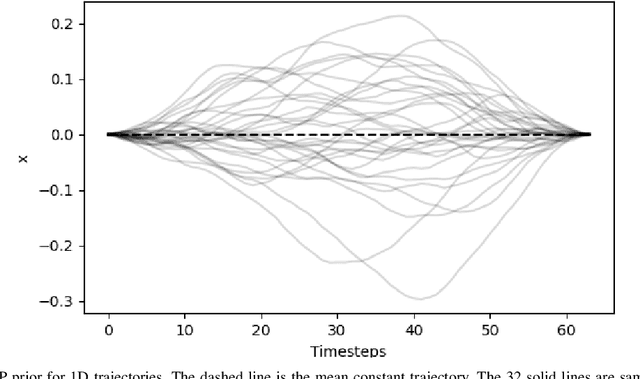
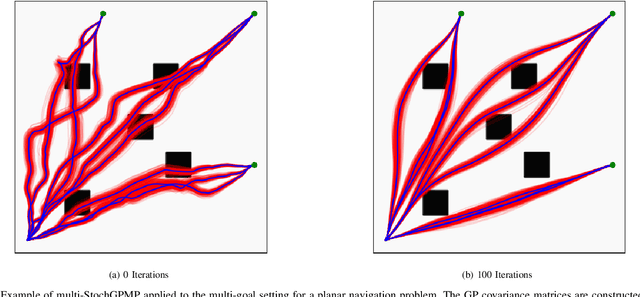
In this paper, we focus on the problem of integrating Energy-based Models (EBM) as guiding priors for motion optimization. EBMs are a set of neural networks that can represent expressive probability density distributions in terms of a Gibbs distribution parameterized by a suitable energy function. Due to their implicit nature, they can easily be integrated as optimization factors or as initial sampling distributions in the motion optimization problem, making them good candidates to integrate data-driven priors in the motion optimization problem. In this work, we present a set of required modeling and algorithmic choices to adapt EBMs into motion optimization. We investigate the benefit of including additional regularizers in the learning of the EBMs to use them with gradient-based optimizers and we present a set of EBM architectures to learn generalizable distributions for manipulation tasks. We present multiple cases in which the EBM could be integrated for motion optimization and evaluate the performance of learned EBMs as guiding priors for both simulated and real robot experiments.

Revisiting Model-based Value Expansion

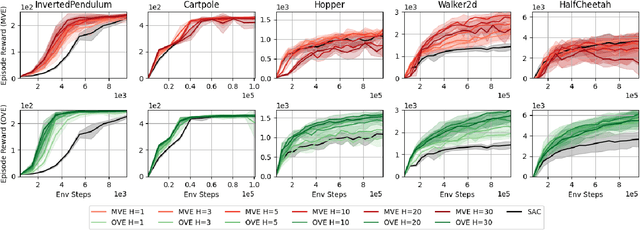
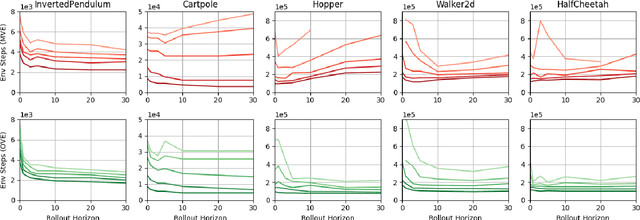
Model-based value expansion methods promise to improve the quality of value function targets and, thereby, the effectiveness of value function learning. However, to date, these methods are being outperformed by Dyna-style algorithms with conceptually simpler 1-step value function targets. This shows that in practice, the theoretical justification of value expansion does not seem to hold. We provide a thorough empirical study to shed light on the causes of failure of value expansion methods in practice which is believed to be the compounding model error. By leveraging GPU based physics simulators, we are able to efficiently use the true dynamics for analysis inside the model-based reinforcement learning loop. Performing extensive comparisons between true and learned dynamics sheds light into this black box. This paper provides a better understanding of the actual problems in value expansion. We provide future directions of research by empirically testing the maximum theoretical performance of current approaches.