Welfare-Centric Clustering

Fair clustering has traditionally focused on ensuring equitable group representation or equalizing group-specific clustering costs. However, Dickerson et al. (2025) recently showed that these fairness notions may yield undesirable or unintuitive clustering outcomes and advocated for a welfare-centric clustering approach that models the utilities of the groups. In this work, we model group utilities based on both distances and proportional representation and formalize two optimization objectives based on welfare-centric clustering: the Rawlsian (Egalitarian) objective and the Utilitarian objective. We introduce novel algorithms for both objectives and prove theoretical guarantees for them. Empirical evaluations on multiple real-world datasets demonstrate that our methods significantly outperform existing fair clustering baselines.

Fair Clustering: Critique, Caveats, and Future Directions

Clustering is a fundamental problem in machine learning and operations research. Therefore, given the fact that fairness considerations have become of paramount importance in algorithm design, fairness in clustering has received significant attention from the research community. The literature on fair clustering has resulted in a collection of interesting fairness notions and elaborate algorithms. In this paper, we take a critical view of fair clustering, identifying a collection of ignored issues such as the lack of a clear utility characterization and the difficulty in accounting for the downstream effects of a fair clustering algorithm in machine learning settings. In some cases, we demonstrate examples where the application of a fair clustering algorithm can have significant negative impacts on social welfare. We end by identifying a collection of steps that would lead towards more impactful research in fair clustering.

Reconstruction Attacks on Machine Unlearning: Simple Models are Vulnerable

Machine unlearning is motivated by desire for data autonomy: a person can request to have their data's influence removed from deployed models, and those models should be updated as if they were retrained without the person's data. We show that, counter-intuitively, these updates expose individuals to high-accuracy reconstruction attacks which allow the attacker to recover their data in its entirety, even when the original models are so simple that privacy risk might not otherwise have been a concern. We show how to mount a near-perfect attack on the deleted data point from linear regression models. We then generalize our attack to other loss functions and architectures, and empirically demonstrate the effectiveness of our attacks across a wide range of datasets (capturing both tabular and image data). Our work highlights that privacy risk is significant even for extremely simple model classes when individuals can request deletion of their data from the model.

Who's in and who's out? A case study of multimodal CLIP-filtering in DataComp

As training datasets become increasingly drawn from unstructured, uncontrolled environments such as the web, researchers and industry practitioners have increasingly relied upon data filtering techniques to "filter out the noise" of web-scraped data. While datasets have been widely shown to reflect the biases and values of their creators, in this paper we contribute to an emerging body of research that assesses the filters used to create these datasets. We show that image-text data filtering also has biases and is value-laden, encoding specific notions of what is counted as "high-quality" data. In our work, we audit a standard approach of image-text CLIP-filtering on the academic benchmark DataComp's CommonPool by analyzing discrepancies of filtering through various annotation techniques across multiple modalities of image, text, and website source. We find that data relating to several imputed demographic groups -- such as LGBTQ+ people, older women, and younger men -- are associated with higher rates of exclusion. Moreover, we demonstrate cases of exclusion amplification: not only are certain marginalized groups already underrepresented in the unfiltered data, but CLIP-filtering excludes data from these groups at higher rates. The data-filtering step in the machine learning pipeline can therefore exacerbate representation disparities already present in the data-gathering step, especially when existing filters are designed to optimize a specifically-chosen downstream performance metric like zero-shot image classification accuracy. Finally, we show that the NSFW filter fails to remove sexually-explicit content from CommonPool, and that CLIP-filtering includes several categories of copyrighted content at high rates. Our conclusions point to a need for fundamental changes in dataset creation and filtering practices.

Initializing Services in Interactive ML Systems for Diverse Users

This paper studies ML systems that interactively learn from users across multiple subpopulations with heterogeneous data distributions. The primary objective is to provide specialized services for different user groups while also predicting user preferences. Once the users select a service based on how well the service anticipated their preference, the services subsequently adapt and refine themselves based on the user data they accumulate, resulting in an iterative, alternating minimization process between users and services (learning dynamics). Employing such tailored approaches has two main challenges: (i) Unknown user preferences: Typically, data on user preferences are unavailable without interaction, and uniform data collection across a large and diverse user base can be prohibitively expensive. (ii) Suboptimal Local Solutions: The total loss (sum of loss functions across all users and all services) landscape is not convex even if the individual losses on a single service are convex, making it likely for the learning dynamics to get stuck in local minima. The final outcome of the aforementioned learning dynamics is thus strongly influenced by the initial set of services offered to users, and is not guaranteed to be close to the globally optimal outcome. In this work, we propose a randomized algorithm to adaptively select very few users to collect preference data from, while simultaneously initializing a set of services. We prove that under mild assumptions on the loss functions, the expected total loss achieved by the algorithm right after initialization is within a factor of the globally optimal total loss with complete user preference data, and this factor scales only logarithmically in the number of services. Our theory is complemented by experiments on real as well as semi-synthetic datasets.

Fair Active Learning in Low-Data Regimes

In critical machine learning applications, ensuring fairness is essential to avoid perpetuating social inequities. In this work, we address the challenges of reducing bias and improving accuracy in data-scarce environments, where the cost of collecting labeled data prohibits the use of large, labeled datasets. In such settings, active learning promises to maximize marginal accuracy gains of small amounts of labeled data. However, existing applications of active learning for fairness fail to deliver on this, typically requiring large labeled datasets, or failing to ensure the desired fairness tolerance is met on the population distribution. To address such limitations, we introduce an innovative active learning framework that combines an exploration procedure inspired by posterior sampling with a fair classification subroutine. We demonstrate that this framework performs effectively in very data-scarce regimes, maximizing accuracy while satisfying fairness constraints with high probability. We evaluate our proposed approach using well-established real-world benchmark datasets and compare it against state-of-the-art methods, demonstrating its effectiveness in producing fair models, and improvement over existing methods.

Scalable Membership Inference Attacks via Quantile Regression

Membership inference attacks are designed to determine, using black box access to trained models, whether a particular example was used in training or not. Membership inference can be formalized as a hypothesis testing problem. The most effective existing attacks estimate the distribution of some test statistic (usually the model's confidence on the true label) on points that were (and were not) used in training by training many \emph{shadow models} -- i.e. models of the same architecture as the model being attacked, trained on a random subsample of data. While effective, these attacks are extremely computationally expensive, especially when the model under attack is large. We introduce a new class of attacks based on performing quantile regression on the distribution of confidence scores induced by the model under attack on points that are not used in training. We show that our method is competitive with state-of-the-art shadow model attacks, while requiring substantially less compute because our attack requires training only a single model. Moreover, unlike shadow model attacks, our proposed attack does not require any knowledge of the architecture of the model under attack and is therefore truly ``black-box". We show the efficacy of this approach in an extensive series of experiments on various datasets and model architectures.

Doubly Constrained Fair Clustering

The remarkable attention which fair clustering has received in the last few years has resulted in a significant number of different notions of fairness. Despite the fact that these notions are well-justified, they are often motivated and studied in a disjoint manner where one fairness desideratum is considered exclusively in isolation from the others. This leaves the understanding of the relations between different fairness notions as an important open problem in fair clustering. In this paper, we take the first step in this direction. Specifically, we consider the two most prominent demographic representation fairness notions in clustering: (1) Group Fairness (GF), where the different demographic groups are supposed to have close to population-level representation in each cluster and (2) Diversity in Center Selection (DS), where the selected centers are supposed to have close to population-level representation of each group. We show that given a constant approximation algorithm for one constraint (GF or DS only) we can obtain a constant approximation solution that satisfies both constraints simultaneously. Interestingly, we prove that any given solution that satisfies the GF constraint can always be post-processed at a bounded degradation to the clustering cost to additionally satisfy the DS constraint while the reverse is not true. Furthermore, we show that both GF and DS are incompatible (having an empty feasibility set in the worst case) with a collection of other distance-based fairness notions. Finally, we carry experiments to validate our theoretical findings.

Multicalibrated Regression for Downstream Fairness

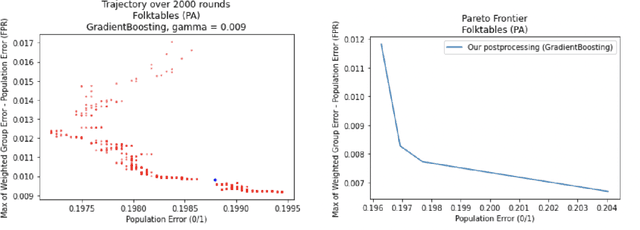
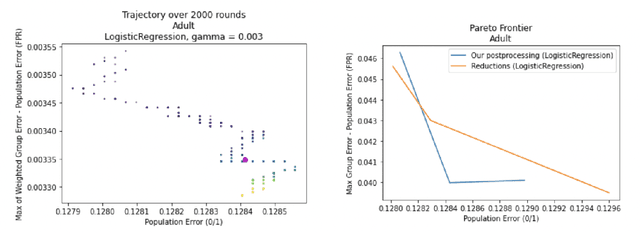
We show how to take a regression function $\hat{f}$ that is appropriately ``multicalibrated'' and efficiently post-process it into an approximately error minimizing classifier satisfying a large variety of fairness constraints. The post-processing requires no labeled data, and only a modest amount of unlabeled data and computation. The computational and sample complexity requirements of computing $\hat f$ are comparable to the requirements for solving a single fair learning task optimally, but it can in fact be used to solve many different downstream fairness-constrained learning problems efficiently. Our post-processing method easily handles intersecting groups, generalizing prior work on post-processing regression functions to satisfy fairness constraints that only applied to disjoint groups. Our work extends recent work showing that multicalibrated regression functions are ``omnipredictors'' (i.e. can be post-processed to optimally solve unconstrained ERM problems) to constrained optimization.

Individual Preference Stability for Clustering

In this paper, we propose a natural notion of individual preference (IP) stability for clustering, which asks that every data point, on average, is closer to the points in its own cluster than to the points in any other cluster. Our notion can be motivated from several perspectives, including game theory and algorithmic fairness. We study several questions related to our proposed notion. We first show that deciding whether a given data set allows for an IP-stable clustering in general is NP-hard. As a result, we explore the design of efficient algorithms for finding IP-stable clusterings in some restricted metric spaces. We present a polytime algorithm to find a clustering satisfying exact IP-stability on the real line, and an efficient algorithm to find an IP-stable 2-clustering for a tree metric. We also consider relaxing the stability constraint, i.e., every data point should not be too far from its own cluster compared to any other cluster. For this case, we provide polytime algorithms with different guarantees. We evaluate some of our algorithms and several standard clustering approaches on real data sets.