High-Altitude Balloon Station-Keeping with First Order Model Predictive Control

High-altitude balloons (HABs) are common in scientific research due to their wide range of applications and low cost. Because of their nonlinear, underactuated dynamics and the partial observability of wind fields, prior work has largely relied on model-free reinforcement learning (RL) methods to design near-optimal control schemes for station-keeping. These methods often compare only against hand-crafted heuristics, dismissing model-based approaches as impractical given the system complexity and uncertain wind forecasts. We revisit this assumption about the efficacy of model-based control for station-keeping by developing First-Order Model Predictive Control (FOMPC). By implementing the wind and balloon dynamics as differentiable functions in JAX, we enable gradient-based trajectory optimization for online planning. FOMPC outperforms a state-of-the-art RL policy, achieving a 24% improvement in time-within-radius (TWR) without requiring offline training, though at the cost of greater online computation per control step. Through systematic ablations of modeling assumptions and control factors, we show that online planning is effective across many configurations, including under simplified wind and dynamics models.

Benchmark Datasets for Lead-Lag Forecasting on Social Platforms

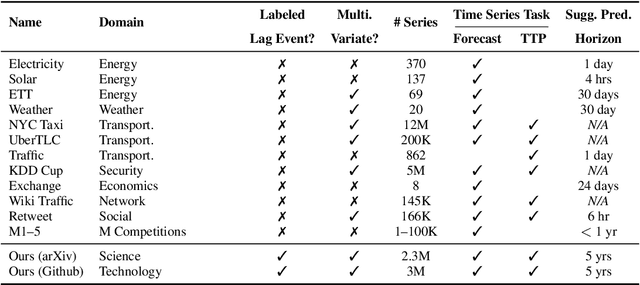
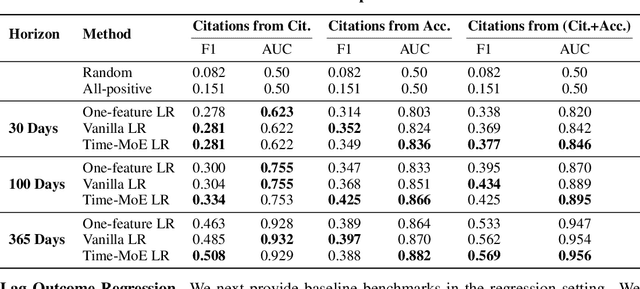
Social and collaborative platforms emit multivariate time-series traces in which early interactions-such as views, likes, or downloads-are followed, sometimes months or years later, by higher impact like citations, sales, or reviews. We formalize this setting as Lead-Lag Forecasting (LLF): given an early usage channel (the lead), predict a correlated but temporally shifted outcome channel (the lag). Despite the ubiquity of such patterns, LLF has not been treated as a unified forecasting problem within the time-series community, largely due to the absence of standardized datasets. To anchor research in LLF, here we present two high-volume benchmark datasets-arXiv (accesses -> citations of 2.3M papers) and GitHub (pushes/stars -> forks of 3M repositories)-and outline additional domains with analogous lead-lag dynamics, including Wikipedia (page views -> edits), Spotify (streams -> concert attendance), e-commerce (click-throughs -> purchases), and LinkedIn profile (views -> messages). Our datasets provide ideal testbeds for lead-lag forecasting, by capturing long-horizon dynamics across years, spanning the full spectrum of outcomes, and avoiding survivorship bias in sampling. We documented all technical details of data curation and cleaning, verified the presence of lead-lag dynamics through statistical and classification tests, and benchmarked parametric and non-parametric baselines for regression. Our study establishes LLF as a novel forecasting paradigm and lays an empirical foundation for its systematic exploration in social and usage data. Our data portal with downloads and documentation is available at https://lead-lag-forecasting.github.io/.

Datasets for Navigating Sensitive Topics in Recommendation Systems

Personalized AI systems, from recommendation systems to chatbots, are a prevalent method for distributing content to users based on their learned preferences. However, there is growing concern about the adverse effects of these systems, including their potential tendency to expose users to sensitive or harmful material, negatively impacting overall well-being. To address this concern quantitatively, it is necessary to create datasets with relevant sensitivity labels for content, enabling researchers to evaluate personalized systems beyond mere engagement metrics. To this end, we introduce two novel datasets that include a taxonomy of sensitivity labels alongside user-content ratings: one that integrates MovieLens rating data with content warnings from the Does the Dog Die? community ratings website, and another that combines fan-fiction interaction data and user-generated warnings from Archive of Our Own.

Pre-trained Large Language Models Learn Hidden Markov Models In-context

Hidden Markov Models (HMMs) are foundational tools for modeling sequential data with latent Markovian structure, yet fitting them to real-world data remains computationally challenging. In this work, we show that pre-trained large language models (LLMs) can effectively model data generated by HMMs via in-context learning (ICL)$\unicode{x2013}$their ability to infer patterns from examples within a prompt. On a diverse set of synthetic HMMs, LLMs achieve predictive accuracy approaching the theoretical optimum. We uncover novel scaling trends influenced by HMM properties, and offer theoretical conjectures for these empirical observations. We also provide practical guidelines for scientists on using ICL as a diagnostic tool for complex data. On real-world animal decision-making tasks, ICL achieves competitive performance with models designed by human experts. To our knowledge, this is the first demonstration that ICL can learn and predict HMM-generated sequences$\unicode{x2013}$an advance that deepens our understanding of in-context learning in LLMs and establishes its potential as a powerful tool for uncovering hidden structure in complex scientific data.

Sub-optimality of the Separation Principle for Quadratic Control from Bilinear Observations

We consider the problem of controlling a linear dynamical system from bilinear observations with minimal quadratic cost. Despite the similarity of this problem to standard linear quadratic Gaussian (LQG) control, we show that when the observation model is bilinear, neither does the Separation Principle hold, nor is the optimal controller affine in the estimated state. Moreover, the cost-to-go is non-convex in the control input. Hence, finding an analytical expression for the optimal feedback controller is difficult in general. Under certain settings, we show that the standard LQG controller locally maximizes the cost instead of minimizing it. Furthermore, the optimal controllers (derived analytically) are not unique and are nonlinear in the estimated state. We also introduce a notion of input-dependent observability and derive conditions under which the Kalman filter covariance remains bounded. We illustrate our theoretical results through numerical experiments in multiple synthetic settings.

Policy Design for Two-sided Platforms with Participation Dynamics

In two-sided platforms (e.g., video streaming or e-commerce), viewers and providers engage in interactive dynamics, where an increased provider population results in higher viewer utility and the increase of viewer population results in higher provider utility. Despite the importance of such "population effects" on long-term platform health, recommendation policies do not generally take the participation dynamics into account. This paper thus studies the dynamics and policy design on two-sided platforms under the population effects for the first time. Our control- and game-theoretic findings warn against the use of myopic-greedy policy and shed light on the importance of provider-side considerations (i.e., effectively distributing exposure among provider groups) to improve social welfare via population growth. We also present a simple algorithm to optimize long-term objectives by considering the population effects, and demonstrate its effectiveness in synthetic and real-data experiments.

Finite Sample Identification of Partially Observed Bilinear Dynamical Systems

We consider the problem of learning a realization of a partially observed bilinear dynamical system (BLDS) from noisy input-output data. Given a single trajectory of input-output samples, we provide a finite time analysis for learning the system's Markov-like parameters, from which a balanced realization of the bilinear system can be obtained. Our bilinear system identification algorithm learns the system's Markov-like parameters by regressing the outputs to highly correlated, nonlinear, and heavy-tailed covariates. Moreover, the stability of BLDS depends on the sequence of inputs used to excite the system. These properties, unique to partially observed bilinear dynamical systems, pose significant challenges to the analysis of our algorithm for learning the unknown dynamics. We address these challenges and provide high probability error bounds on our identification algorithm under a uniform stability assumption. Our analysis provides insights into system theoretic quantities that affect learning accuracy and sample complexity. Lastly, we perform numerical experiments with synthetic data to reinforce these insights.

Learning Linear Dynamics from Bilinear Observations

We consider the problem of learning a realization of a partially observed dynamical system with linear state transitions and bilinear observations. Under very mild assumptions on the process and measurement noises, we provide a finite time analysis for learning the unknown dynamics matrices (up to a similarity transform). Our analysis involves a regression problem with heavy-tailed and dependent data. Moreover, each row of our design matrix contains a Kronecker product of current input with a history of inputs, making it difficult to guarantee persistence of excitation. We overcome these challenges, first providing a data-dependent high probability error bound for arbitrary but fixed inputs. Then, we derive a data-independent error bound for inputs chosen according to a simple random design. Our main results provide an upper bound on the statistical error rates and sample complexity of learning the unknown dynamics matrices from a single finite trajectory of bilinear observations.

Harm Mitigation in Recommender Systems under User Preference Dynamics

We consider a recommender system that takes into account the interplay between recommendations, the evolution of user interests, and harmful content. We model the impact of recommendations on user behavior, particularly the tendency to consume harmful content. We seek recommendation policies that establish a tradeoff between maximizing click-through rate (CTR) and mitigating harm. We establish conditions under which the user profile dynamics have a stationary point, and propose algorithms for finding an optimal recommendation policy at stationarity. We experiment on a semi-synthetic movie recommendation setting initialized with real data and observe that our policies outperform baselines at simultaneously maximizing CTR and mitigating harm.

Random Features Approximation for Control-Affine Systems

Modern data-driven control applications call for flexible nonlinear models that are amenable to principled controller synthesis and realtime feedback. Many nonlinear dynamical systems of interest are control affine. We propose two novel classes of nonlinear feature representations which capture control affine structure while allowing for arbitrary complexity in the state dependence. Our methods make use of random features (RF) approximations, inheriting the expressiveness of kernel methods at a lower computational cost. We formalize the representational capabilities of our methods by showing their relationship to the Affine Dot Product (ADP) kernel proposed by Casta\~neda et al. (2021) and a novel Affine Dense (AD) kernel that we introduce. We further illustrate the utility by presenting a case study of data-driven optimization-based control using control certificate functions (CCF). Simulation experiments on a double pendulum empirically demonstrate the advantages of our methods.